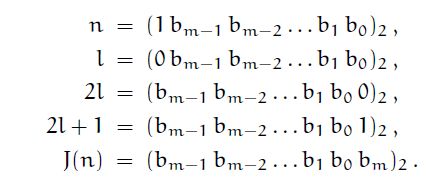暑期刷题记录
已经决定不玩空间了,在这里开一贴,用来记录暑假期间刷过的每一题。
时间从7.29号开始计算。
1. HDU 4883 TIANKENG’s restaurant ( 贪心 )
这个是bestcoder #2 的第一题,,居然想半天没有做出来,简直是太弱了,居然又在分情况讨论 题目大意:TIANKENG的饭店有客人陆续到达,如果再一批客人没有走的情况下,新来的客人就需要另外的座位,问最少需要多少座位。 题解: 贪心算法,首先对所有时间进行排序(时间相同以人数为第二关键字), 然后如果是到达,加上该人数,如果是离开,减去该人数,然后从头到尾扫一遍找到最大值。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define maxn 10010 6 7 struct node 8 { 9 int time; 10 int peo; 11 }E[maxn<<1]; 12 13 int cmp(node x,node y) 14 { 15 if(x.time != y.time) return x.time < y.time; 16 else return x.peo < y.peo; 17 } 18 int t,n,a,b,c,d,p; 19 20 int main() 21 { 22 scanf("%d",&t); 23 while(t--) 24 { 25 int cnt = 0; 26 scanf("%d",&n); 27 for(int i=0;i<n;i++) 28 { 29 scanf("%d %d:%d %d:%d",&p,&a,&b,&c,&d); 30 E[cnt].peo = p; 31 E[cnt++].time = a*60 + b; 32 E[cnt].peo = -p; 33 E[cnt++].time = c*60 + d; 34 } 35 sort(E,E+cnt,cmp); 36 int res = 0; 37 int put = -1; 38 for(int i=0;i<cnt;i++) 39 { 40 res += E[i].peo; 41 if(res > put) put = res; 42 } 43 printf("%d\n",put); 44 } 45 return 0; 46 }
2. HDU 4521 小明系列问题――小明序列 ( 线段树 + dp思想 )
题目大意: 给出一个序列,找出这个序列的"小明序列"所需要的元素的个数。小明序列的要求: 是原序列的递增子序列,并且子序列中相邻元素的下标为d 思路: 线段树 + dp思想来更新(无奈dp思想太弱了) 线段树的域 Max[] 用来存放当前结点结束的Sub序列的最大元素个数, 从下标 d + 1 开始更新,
#include <cstdio> #include <cstring> #include <algorithm> #define lson l, m, rt << 1 #define rson m + 1, r, rt << 1 | 1 #define mid(l,r) (l + r) >> 1 #define maxn 101000 #define inf 0x3f3f3f3f using namespace std; int Max[maxn<<2]; int d, n, s[maxn], dp[maxn], res, len; void PushUp(int rt) { Max[rt] = max(Max[rt<<1], Max[rt<<1|1]); } void Build(int l,int r,int rt) { Max[rt] = 0; if(l == r) return; int m = mid(l,r); Build(lson); Build(rson); } void Update(int pos,int val,int l,int r,int rt) { if(l == r) { Max[rt] = max(val,Max[rt]); return; } int m = mid(l,r); if(pos <= m) Update(pos,val,lson); else Update(pos,val,rson); PushUp(rt); } int Query(int L,int R,int l,int r,int rt) { if(L <= l && r <= R) return Max[rt]; int m = mid(l,r); int t1 = -inf; int t2 = -inf; if(L <= m) t1 = Query(L,R,lson); if(R > m) t2 = Query(l,R,rson); return max(t1,t2); } int main() { while(~scanf("%d %d",&n,&d)) { res = len = 0; for(int i=1;i<=n;i++) { scanf("%d",&s[i]); len = max(s[i],len); } Build(0,len,1); for(int i=1;i<=n;i++) { //从d + 1 位置开始更新 if(i > d + 1) Update(s[i-d-1],dp[i-d-1],0,len,1); //状态转移时,查询比当前值小(即s[i]-1)的最大值 if(s[i] > 0) dp[i] = Query(0,s[i]-1,0,len,1) + 1; else dp[i] = 1; res = max(res,dp[i]); } printf("%d\n",res); } return 0; }
3. HDU 4884 TIANKENG’s rice shop ( 模拟 / 感觉有点复杂 )
这个故事告诉我们题目一定要读清楚再开始思考问题。
题意没有理解清楚。。
题目意思 参考这里
具体模拟就是,每读取一个顾客的购买信息,如果是在最后一次炒饭之前进来的,先检查是否有剩余,如果有剩余且剩余大于本次所需,就可以在最后一次炒饭结束之后离开,否则需要更新剩余的数量和最后一次炒饭的时间。
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define maxn 1111 #define maxtime 24*60 #define clr(a,b) memset(a,b,sizeof(a)) int t,k,m,n,T,hh,mm,id,num; int cnt[maxn], last[maxn]; void print(int time) { if(time >= maxtime) time %= maxtime; printf("%02d:%02d\n", time / 60, time % 60); } int main() { // freopen("1.txt","r",stdin); scanf("%d",&T); while(T--) { scanf("%d %d %d %d",&n,&t,&k,&m); clr(cnt,0); int cur = 0, next = 0; for(int i=0;i<m;i++) { scanf("%d:%d %d %d",&hh,&mm,&id,&num); next = hh * 60 + mm; if(cnt[id] >= num && last[id] >= next) { cnt[id] -= num; print(last[id] + t); continue; } if(cnt[id] && last[id] >= next) { num -= cnt[id]; } int x = (num - 1) / k + 1; cur = max(cur,next) + t * x; print(cur); cnt[id] = x * k - num; last[id] = cur - t; } if(T) puts(""); } return 0; }
4. UVA 10474 Where is the marble? ( STL / sort + lower_bound() 二分查找 )
读懂题目可以轻松AC,不过题目绕来绕去真的很长。
题目大意就是: 给定一个序列,先进行排序然后再进行Q租询问,输出的结果是某个值在序列中的位置,没有则输出不存在。
函数lower_bound()在first和last中的前闭后开区间进行二分查找
返回大于或等于val的第一个元素位置。如果所有元素都小于val,则返回last的位
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; int q, n, x[10010], val, cas = 1; int main() { while(~scanf("%d %d",&n,&q) && (n+q)) { for(int i=0;i<n;i++) scanf("%d",&x[i]); sort(x,x+n); printf("CASE# %d:\n",cas++); while(q--) { scanf("%d",&val); int pos = lower_bound(x,x+n,val) - x; if(x[pos] == val) printf("%d found at %d\n",val,pos+1); else printf("%d not found\n",val); } } return 0; }
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; int N,Q,cas,x[11111],key; int bs(int l,int r,int key) { while(l <= r) { int m = (l + r)>>1; if(key == x[m]) { for(int i=m-1;;i--) { if(x[i] != x[i+1]) return i+1; } } else if(key < x[m]) r = m - 1; else l = m + 1; } return -1; } int main() { cas = 1; while(~scanf("%d %d",&N,&Q)) { if(N ==0 && Q == 0) break; for(int i=0;i<N;i++) scanf("%d",&x[i]); sort(x,x+N); printf("CASE# %d:\n",cas++); for(int i=0;i<Q;i++) { scanf("%d",&key); int ret = bs(0,N-1,key); if(ret != -1) printf("%d found at %d\n",key,ret+1); else printf("%d not found\n",key); } } return 0; }
5. UVA 1339 - Ancient Cipher ( 坑爹题 / 凯撒加密 + 乱序加密 )
这道题我搞了1个多小时还是在WA,,后来发现是自己的想法有问题。
这道题目的正确解法,,,参看这个博客吧。。。
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define clr(a,b) memset(a,b,sizeof(a)) char b[110], a[110], len; int Hash[256]; /* bool substitution(char* a,char* b) { char x[110], y [110]; strcpy(x,a); strcpy(y,b); for(int i=0;x[i];i++) { x[i]--; if(x[i] < 'A') x[i] = 'Z'; if(x[i] != y[i]) return false; } return true; } bool permutation(char* a,char* b) { char x[110], y [110]; strcpy(x,a); strcpy(y,b); int len = strlen(x); sort(x,x+len); sort(y,y+len); if(strcmp(x,y) == 0) return true; return false; } bool combination(char* a,char* b) { char x[110], y [110]; strcpy(x,a); strcpy(y,b); int cnt = 0; for(int i=0;x[i];i++) { x[i]--; if(x[i] < 'A') x[i] = 'Z'; cnt++; } sort(x,x+cnt); sort(y,y+cnt); for(int i=0;a[i];i++) { if(x[i] != y[i]) return false; } return true; } */ //思路错误,,谁告诉你sort之后a[i] 一定和 b[i] 对应? bool check() { sort(a,a+len); sort(b,b+len); clr(Hash,0); //printf("\n%s\n%s\n\n",a,b); if(strcmp(a,b) == 0) return true; else { for(int i=0;i<len;i++) if(Hash[a[i]] == 0) Hash[a[i]] = b[i]; for(int i=0;i<len;i++) { a[i] = Hash[a[i]]; } // printf("\n%s\n%s\n\n",a,b); if(strcmp(a,b) == 0) return true; return false; } } int main() { while(~scanf("%s %s",a,b)) { len = strlen(a); if(check()) puts("YES"); else puts("NO"); } return 0; }
#include <cstdio> #include <cstring> #include <algorithm> #define clr(a,b) memset(a,b,sizeof(a)) using namespace std; char a[110], b[110]; int ca[26], cb[26]; int main() { while(~scanf("%s %s",a,b)) { clr(ca,0), clr(cb,0); for(int i=0;a[i];i++) { ca[a[i] - 'A']++; cb[b[i] - 'A']++; } sort(ca,ca+26); sort(cb,cb+26); if(memcmp(ca,cb,sizeof(ca)) == 0) puts("YES"); else puts("NO"); } return 0; }
6. UVA 133 - the Dole Queue ( 模拟 / 类似约瑟夫环 )
这道题WA一发,PE一发,,思路是没有问题,就是模拟选择,这题数据很小,也可以用循环链表来做。
就是题目一定要看清楚还有就是输出格式。
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; int x[22], n, k, m; int main() { while(~scanf("%d %d %d",&n,&k,&m) && (n + k + m)) { for(int i=1;i<=n;i++) x[i] = i; int st = 0, et = n + 1, cnt = n; while(cnt) { for(int i=0;i<k;i++) { st++; if(st > n) st -= n; while(x[st] == -1) { st++; if(st > n) st -= n; } } for(int i=0;i<m;i++) { et--; if(et < 1) et += n; while(x[et] == -1) { et--; if(et < 1) et += n; } } if(st == et) { printf("%3d",x[st]); cnt--; x[st] = -1; } else { printf("%3d%3d",x[st],x[et]); cnt -= 2; x[st] = -1, x[et] = -1; } if(cnt) printf(","); } puts(""); } return 0; }
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; int x[22], n, k, m; int main() { while(~scanf("%d %d %d",&n,&k,&m) && (n + k + m)) { for(int i=0;i<n;i++) x[i] = i+1; int st = -1, et = n, cnt = n; while(cnt) { for(int i=0;i<k;i++) { st++; st = (st + n) % n; while(x[st] == -1) { st++; st = (st + n) % n; } } for(int i=0;i<m;i++) { et--; et = (et + n) % n; while(x[et] == -1) { et--; et = (et + n) % n; } } if(st == et) { printf("%3d",x[st]); cnt--; x[st] = -1; } else { printf("%3d%3d",x[st],x[et]); cnt -= 2; x[st] = -1, x[et] = -1; } if(cnt) printf(","); } puts(""); } return 0; }
7. UVA 213 - Message Decoding ( 模拟 / 二进制 + 加解密对应 )
这题我搞了一个下午,结果还没搞出来,晕 题目意思是编写一个解码程序。首先输入一个编码头,题目已经给定了对应关系 (例如 AB#TANCnrtXc A对应0 B对应00 #对应01 T对应10 A又对应000 一次类推) 然后给出一个编码过后的文本串。只由'0' 和 '1' 组成 然后需要根据编码头将密文翻译为明文
题目例子:
编码头为 $#**\ 编码文本 0100000101101100011100101000 取前三位 010 -> 2 字段长度为2 依次取2位。得00 00 10 11 也就是 # # * (11表示这个segment结束) 再取三位 011 -> 3 字段长度为3 依次取2位 得 000 111 也就是 \ (111表示这个segment结束) 再取三位 001 -> 1 字段长度为1 依次取1位 得 0 1 也就是 $ (1表示这个segment结束) 最后取到 000 结束 最终解码为 ##*\$
#include <cstdio> #include <cstring> #include <algorithm> #include <string> #include <iostream> #define clr(a,b) memset(a,b,sizeof(a)) using namespace std; int Map[8][1<<8]; int readchar() { while(true) { int ch = getchar(); if(ch != '\r' && ch != '\n') return ch; } } int readint(int l) { int ret = 0; while(l--) { ret = (ret << 1) + readchar() - '0'; } return ret; } bool read_header() { clr(Map,0); Map[1][0] = readchar(); for(int len = 2; len <= 7; len++) { for(int i = 0; i < (1<<len) - 1; i++) { int ch = getchar(); if(ch == EOF) return false; if(ch == '\n' || ch =='\r') return true; Map[len][i] = ch; } } return true; } int main() { while(read_header()) { while(true) { int len = readint(3); if(len == 0) break; while(true) { int v = readint(len); if(v == (1 << len) - 1) break; putchar(Map[len][v]); } } putchar('\n'); } return 0; }
8. POJ 1781 - In Danger ( 数学/ 递推 / 约瑟夫环问题 )
这道题是裸的约瑟夫环问题,在具体数学上有很详细的说明。 在k = 2的情况下。 有公式 J( 2^m + l ) = 2*l + 1; 具体证明在具体数学上面写得很清楚 可以通过先模拟,打表找规律,最后用数学归纳法证明 因为k = 2
N 1 2 3 4 5 6 7 8 9
J 1 1 3 1 3 5 7 1 3
如果直接模拟,时间复杂度为O(M*N)
推出公式,可以在O(1)
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; char str[5]; int main() { while(~scanf("%s",str)) { if(strcmp(str,"00e0") == 0) break; int n = (str[0]-'0') * 10 + str[1] - '0'; for(int i=0;i<str[3] - '0';i++) n *= 10; int t = 1; for(int i=0; (t<<1) <= n; i++) t <<= 1; t = n - t; printf("%d\n",(t<<1) + 1); } return 0; }
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; char str[5]; int main() { while(~scanf("%s",str)) { if(strcmp(str,"00e0") == 0) break; int n = (str[0]-'0') * 10 + str[1] - '0'; for(int i=0;i<str[3] - '0';i++) n *= 10; int t = 1 << 31; while((n&t) == 0) t >>= 1; n = ((n&(~t))<<1)|1; printf("%d\n",n); } return 0; }
9. HDU 2925 Musical Chair ( 数学/ 递推 / 约瑟夫环问题 )
具体数学上介绍并且推导了 k = 2 时候的约瑟夫环问题 当然还有当人数为K = M时的情况。 这里我们得到递推公式 假设 k = 3,N = 9,W = 0
第一个被杀的坑定是3(也就是k) W = 3
N 1 2 3 4 5 6 7 8 9 N 4 5 6 7 8 9 1 2
V S S X S S S S S S V S S X S S S S S
N 7 8 9 1 2 4 5 N 1 2 4 5 7 8
V S S X S S S S V S S X S S S
N 5 7 8 1 2 N 1 2 5 7
V S S X S S V S S X S
N 7 1 2 N 7 1
V S S X V X S
N 1
V S
再来考虑一般的情况
N 1 2 3 4 5 6 7 8 9 N 4 5 6 7 8 9 1 2
V S S X S S S S S S V S S X S S S S S
第一次数值4的下标W1 = 3 (W从0开始)
第二次数值4的下标W2 = 0 W1 = ( W2 + 3 ) % 9 = (0 + 3) % 9 = 3 也就是W1 = ( W2 + k ) % N
第三次数值4的下标W3 = 5 W2 = ( W3 + 3) % 8 = (5 + 3) % 8 = 0 也就是W2 = ( W3 + k ) % (N-1)
这就是一般情况,相邻的两个相同数的下标关系
最后一次,只剩下没有被杀的幸存者,下标必然是0
那么这里就可以考虑往前推了(从后往前推)
核心算法: int ans=0; //存活人最后的序号W为0
for(i=2;i<=n;i++) ans = (ans+k)%i;
因为题目是下标为1开始,所以最后答案 + 1 即可
#include <cstdio> int main() { int n,d,w; while(~scanf("%d %d",&n,&d) && (n+d)) { w = 0; for(int i=2;i<=n;i++) w = (d + w) % i; printf("%d %d %d\n",n,d,w+1); } }
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef struct node { int x; node* next; }J; node* Tail = NULL; node* Head = NULL; node* pos = NULL; int N,K; node* Create(int x) { node* t = new node; t->x = x; t->next = NULL; return t; } void Link(node* t) { if(Head == NULL) Head = Tail = t; else { Tail->next = t; Tail = t; Tail->next = Head; } } int main() { while(scanf("%d %d",&N,&K)) { Head = Tail = NULL; for(int i=1;i<=N;i++) { node* t = Create(i); Link(t); } pos = Tail; int cnt = 0; while(cnt<N-1) { for(int i=1;i<K;i++) { pos = pos->next; } pos->next = pos->next->next; cnt++; } printf("%d\n",pos->x); } return 0; }
10. HDU 1207 汉诺塔Ⅱ ( 数学/ 递推 / hanoi问题)
这道题实际上是要用到dp思想。。 我一开始在那里推啊推推了个递推公式出来,,H[i] = 2*H[i-2] +3 后来发现不是最优的 这个问题是四柱汉诺塔问题。 前人研究出了递推公式,还有r值的确定
引言 汉诺塔算法一直是算法设计科目的最具代表性的研究问题,本文关注于如何设计多柱汉诺塔最优算法的探究。最简单的汉诺塔是三个柱子(A、B、C),因此多柱汉诺塔的柱子个数M≥3。下面从三柱汉诺塔说起,慢慢深入我们要关心的问题。 1. 三柱汉诺塔 三柱汉诺塔是经典的汉诺塔问题,在算法设计中是递归算法的典型问题。其算法是这样的: 首先把A 柱上面的n- 1 个碟子通过C 柱移到B 柱上【T(n-1)步】,然后把A 柱剩下的一个碟子移到C 柱上【1步】, 最后把B 柱上所有的碟子通过A 柱移到C 柱上【T(n-1)步】。很容易得到算法的递归方程为:T(n)=2*T(n-1)+1,因此,不难算出步数是T(n)=2^n-1。对于三柱汉诺塔的算法的正确性自然是毫无争议的,我们需要的是从三柱汉诺塔的设计中引申出多柱汉诺塔的设计方法。 2. 四柱汉诺塔 四柱汉诺塔并不是仅仅是多了一根柱子那么简单,所以我们先尝试从正常的思维出发来探究如何使移动步数最少。 首先我们会想到,三柱汉诺塔需要借助另一个柱子存放前n-1个盘子,再把第n个盘子移动到目的位置。顺其自然的,四柱汉诺塔由于多了一个柱子,所以移动起来就更方便了,我们可以多留下一个盘子n-2,而不让它借位到其他柱子直接移动到目的位置。这样我们就得出算法的基本流程: (1) 从A借助C、D将 n-2个盘子移动到B上。 (2) 将n-2移动到C上。 (3) 将n-1移动到D上。 (4) 将n-2移动到D上。 (5) 从B借助A、C将 n-2个盘子移动到D上。 另外,这么设计是符合正常思维原则的。以为随着柱子的个数增多,我们希望每次移动的时候盘子尽可能不发生折叠,也就是说我们希望除了需要借助存放n-2个盘子的柱子。那么剩下的两个柱子可以允许至多两个盘子不发生折叠就能直接移动到目的位置,这样才使得移动起来比较方便,步骤也会比较少。事实真的是如此吗?我们具体分析一下算法。 按照以上设计的算法流程,我们得到递归方程:F(n)=2*F(n-2)+3。因此得到移动步数为:F(n)=4*2^(n/2)-3:n为奇数;F(n)=6*2^(n/2-1)-3:n为偶数。下边列出6个盘子的移动步数: n 1 2 3 4 5 6 F(n) 1 3 5 9 13 21 到这里,我们已经看出我们的设计的算法已经和经典的汉诺塔算法几乎如出一辙了,甚至是如此的对称和谐!基于此我们甚至可以推广到M(M≥3)个柱子的情况,来得到我们希望的最优解,假设柱子编号为1,2,3…M算法主题框架流程应该如下: (1) 从1柱借助3…M柱子将n-(M-2)个盘子移动到2柱上。 (2) 将M-2个通过3…M-1柱简单的移动到M柱上【2*(M-2)-1步骤】。 (3) 从2柱借助1,3…M-1柱子将n-(M-2)个盘子移动到M柱上。 具体步骤和四柱类似,不再做具体分析。这样我们看到我们自己亲手构建的算法模式如此完美,我们甚至不忍心去破坏它。但是我很遗憾的告诉自己,这种算法虽然正确,却不是最优!!!比如,对于6个盘子4个柱子的汉诺塔,按照我们的想法是保留2个盘子进行移动。现在假如我们保留3个盘子,因此上边的三个盘子按照4柱汉诺塔规则移动到B,步数应该是5(已经算出,可以验证),剩下三个盘子按照3柱汉诺塔规则移动到D上,步数应该是2^3-1=7步,然后B上的三个盘子移动到D上仍然是5步,总步数为5+7+5=17步<21步!现在我们可以确信的告诉自己,我们的想法太“天真”了。虽然我们想到让盘子尽量不发生重叠来保证步数的最少,但是这并不能绝对保证。或许在盘子较少的情况下是可行的,但是盘子增多时,那些多余的只有一个盘子的柱子是可以加以利用的。虽然这么做加多了每次的移动步数,但是却从另一个侧面减少了递归的数量,因此我们需要从这里边找一个平衡点。 从上边的例子中,我们得到一个启示:在递归程序中剩余盘子的个数并不一定是M-2,也有可能是M-1,我们假设剩余盘子是M-r,那么r到底取得多少才合适呢?其实,早在1941年,一位名叫J. S. Frame的人在《美国数学月刊》上提出了一种解决四柱汉诺塔问题的算法,这是人们熟知的Frame算法: (1)用4柱汉诺塔算法把A柱上部分的n- r个碟子通过C柱和D柱移到B柱上【F( n- r )步】。 (2)用3柱汉诺塔经典算法把A柱上剩余的r个碟子通过C柱移到D柱上【2^r-1步】。 (3)用4柱汉诺塔算法把B柱上的n-r个碟子通过A柱和C柱移到D柱上【F(n-r)步】。 (4)依据上边规则求出所有r(1≤r≤n)情况下步数f(n),取最小值得最终解。 因此Frame算法的递归方程如下: F(n)=min(2*F(n-r)+2^r-1),(1≤r≤n)。 通过这个方程我们能得到所有4柱汉诺塔的步骤个数,同时也有人证明[1]了,对于四柱汉诺塔,当r=(sqrt(8*n+1)-1)/2时,能保证f(n)取得最小值F(n)=(n-(r^2-r+2)/2)*2^r+1。所以算法的复杂度是F(n)=O(sqrt(2*n)*2^ sqrt(2*n))。从这这个方程中也可以看出,在n<6的时候,我们可以验证是和我们起初的构想的结构是相同的,但是当n再增多时就不是当初想的那样了。 3. 多柱汉诺塔 基于四柱汉诺塔的Frame算法,我们可以引申到多柱(M柱)汉诺塔的情况,我们简称M柱汉诺塔算法: (1)用M柱汉诺塔算法把1柱上部分的n-r个碟子通过3…M柱移到2柱上【M( n- r )步】。 (2)用M-1柱汉诺塔算法把1柱上剩余的r个碟子通过3…M-1柱移到M柱上【<M-1>(r)步】。 (3)用M柱汉诺塔算法把2柱上的n-r个碟子通过1柱和3…M柱移到M柱上【M( n- r )步】。 (4)依据上边规则求出所有r(1≤r≤n)情况下步数m(n),取最小值得最终解M(n)。 从4柱汉诺塔的递归方程和结果公示中我们可以看出,随着柱子数量的增加,算法的复杂程度也是不断地增加。对于解决M柱汉诺塔问题需要使用M-1柱汉诺塔的算法,因此除了算法解决问题需要递归外,算法的流程本身也需要递归,这种递归结构已经远远地复杂于当前所接触的递归算法。如果有兴趣可以尝试去设计这种算法,算法所涉及的参数应该有盘子的个数n、柱子的个数m、算法的编号num、参数r等信息。因为需要根据不同柱子情况下通过循环和递归找出最合适的r值,所以这种算法的复杂度肯定相当高。不过我们仅仅是为了探究如何取得最优算法,所以具体实现就不再赘述了。 总结 通过以上的讨论,我们从一般的思维——不折叠盘子,出发去找多柱汉诺塔的最优解,但是结果并没有成功——盘子多时有可能柱子没有充分利用。后来通过前人提出的Frame算法引申出多柱汉诺塔算法,并大致描述了多柱汉诺塔算法的双重嵌套递归结构——算法问题的递归以及算法本身的递归实现。这种罕见的递归程序结构给我们在算法设计方面开阔了新的视野,希望不久的将来能找到更好地算法设计方法来解决多柱汉诺塔的问题。 参考文献 1.《四柱汉诺塔之初步探究》杨楷 徐川( 北京大学计算机科学与技术系, 北京, 100871) 北京大学学报( 自然科学版) , 第40 卷, 第1 期, 2004 年1 月
Frame算法的递归方程如下:
F(n)=min(2*F(n-r)+2^r-1),(1≤r≤n)。
通过这个方程我们能得到所有4柱汉诺塔的步骤个数,同时也有人证明[1]了
对于四柱汉诺塔,当r=(sqrt(8*n+1)-1)/2时,能保证f(n)取得最小值F(n)=(n-(r^2-r+2)/2)*2^r+1。
所以算法的复杂度是F(n)=O(sqrt(2*n)*2^ sqrt(2*n))。
从这这个方程中也可以看出,在n<6的时候,我们可以验证是和我们起初的构想的结构是相同的,但是当n再增多时就不是当初想的那样了。
#include <cstdio> #include <cstring> #include <algorithm> #include <cmath> using namespace std; #define ull unsigned long long ull bit[65] = {1}; int n; void init_bit() { for(int i=1;i<65;i++) bit[i] = bit[i-1] << 1; } int hanoi(int n) { int ret = 0, r; if(n == 1) return 1; r = (int)(sqrt(8*n+1)-1)/2; ret += bit[r] - 1; ret += 2*hanoi(n-r); return ret; } int main() { init_bit(); while(~scanf("%d",&n)) printf("%d\n",hanoi(n)); return 0; }
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define ull unsigned long long ull dp[65] = {0,1,3}; ull bit[65] = {1}; int n; void init_bit() { for(int i=1;i<65;i++) { bit[i] = bit[i-1] << 1; } } void init_hanoi() { init_bit(); for(int i=3;i<=64;i++) { dp[i] = bit[i] - 1; for(int j=1;j<i;j++) { if(dp[i-j]*2 + bit[j] - 1 < dp[i]) dp[i] = dp[i-j]*2 + bit[j] - 1; } } } int main() { init_hanoi(); while(~scanf("%d",&n)) printf("%lld\n",dp[n]); return 0; }
11. HDU 2064 汉诺塔Ⅲ ( 数学/ 递推 / hanoi问题)
汉诺塔一并没有找到,而汉诺塔Ⅱ是四柱汉诺塔问题, 递推公式是F(n) = min( 2*F(n-r) + 2^r - 1 ) ( 1<= r <= n ) 本题是汉诺塔Ⅲ,在汉诺塔原来的基础上又增加了约束条件。 即A,B,C三个柱子,A不能直接移动到C,必须经过中间的辅助柱子 这里还是用递推来推出公式 1. 将n-1 块盘子 从A柱借助B柱移动到C柱 F(n-1) 2. 将n从A移动到B 1
3. 将n-1 块盘子 从C柱借助B柱移动到A柱 F(n-1)
4. 将n从B移动到C 1
5. 将n-1 块盘子 从A柱借助B柱移动到C柱 F(n-1)
那么,可以推出递推式:
F(n) = F(n-1)* 3 + 2
#include <cstdio> __int64 dp[36] = {0,2}; int n; void init() { for(int i=2;i<=35;i++) { dp[i] = dp[i-1]*3 + 2; } } int main() { init(); while(~scanf("%d",&n)) { printf("%I64d\n",dp[n]); } return 0; }
12. HDU 2077 汉诺塔Ⅳ ( 数学/ 递推 / hanoi问题)
汉诺塔一路下来,感觉挺有意思的。 还是再次回顾下,最原始的汉诺塔问题, 公式F(n) = 2^n - 1 四柱汉诺塔,封闭公式记不住了,递推公式 F(n) = min(F((n-r)*2 + 2^r -1) 然后是汉诺塔Ⅲ,有限制的汉诺塔问题,同样是递推,公式F(n) = F(n-1)*3 + 2 这题是汉诺塔Ⅲ的再加强版本、 最后推出的公式是 F(n) = F(n-1)*3 - 2 具体的解释我直接放一个blog,orz一下他。。猜的功夫好强
#include <cstdio> int n, t; int main() { scanf("%d",&t); while(t--) { scanf("%d",&n); int x = 1; while(n-- > 1) { x *= 3; } printf("%d\n",x+1); } return 0; }
#include <cstdio> __int64 dp[20] = {0,2}; int n, t; void init() { for(int i=2;i<=20;i++) { dp[i] = dp[i-1]*3 - 2; } } int main() { init(); scanf("%d",&t); while(t--) { scanf("%d",&n); printf("%I64d\n",dp[n]); } return 0; }
13. HDU 1995 汉诺塔Ⅴ ( 数学/ 递推 / hanoi问题)
题目大意: 对于汉诺塔问题,告之盘子总数和盘号,计算该盘子的移动次数.
直接推一下,可以得到规律 n = 1 1 1号盘移动一次 n = 2 2 1 1号盘移动两次,2号盘移动一次 n = 3 4 2 1 1号盘移动四次,2号盘移动二次,3号盘移动四次
那么给定n = N 第i号盘移动的次数就为 2^(N-i)次
也可以表示为 1<<(N-i)
#include <cstdio> int n, m, t; int main() { scanf("%d",&t); while(t--) { scanf("%d %d",&n,&m); printf("%I64d\n",((__int64)1) << (n-m)); } return 0; }
14. HDU 1996 汉诺塔Ⅵ ( 数学/ 递推 / hanoi问题)
题目大意:对于每组数据,输出移动过程中所有会产生的系列总数。 我表示我一看到题目就觉得公式是 3^n。。
#include <cstdio> int n, t; int main() { scanf("%d",&t); while(t--) { scanf("%d",&n); __int64 x = 1; for(int i=0;i<n;i++) x *= 3; printf("%I64d\n",x); } return 0; }
15. HDU 1997 汉诺塔Ⅶ ( 数学/ 递推 / hanoi问题)
从汉诺塔Ⅵ可以知道,汉诺塔移动过程中,全部状态有3^n种。其中有些状态是错误的(没有必要移动的)
本题给出一个状态,然后判断这个状态是否是正确的。(是否是最小移动次数中的某个状态)
思路就看这个吧。
假设第n个盘子符合要求,则判别的下一个目标是第n-1个盘子。
若第n个盘子在A柱上,此时剩余n-1个盘子必由A柱移动到B柱,其中经过了C柱。也就是,第n-1个盘子只能在B,不能在C
若第n个盘子在C住上,这剩余n-1个盘子则是在B柱上,经由A柱,移动到C柱上,因此,A柱就是第n-1个盘子不可能出现的位置。
这里用的dfs从n开始往前搜 注意交换A,B,C柱在dfs中的位置
#include <cstdio> #include <cstring> #define clr(a,b) memset(a,b,sizeof(a)) int n,t,k; int A[70], B[70], C[70]; bool dfs(int n,int* A,int* B,int* C) { if(n == 0) return true; if(*B && *B == n) return false; if(*A && *A == n) return dfs(n-1,++A,C,B); if(*C && *C == n) return dfs(n-1,B,A,++C); } int main() { scanf("%d",&t); while(t--) { clr(A,0); clr(B,0), clr(C,0); scanf("%d",&n); scanf("%d",&k); for(int i=0;i<k;i++) scanf("%d",&A[i]); scanf("%d",&k); for(int i=0;i<k;i++) scanf("%d",&B[i]); scanf("%d",&k); for(int i=0;i<k;i++) scanf("%d",&C[i]); if(dfs(n,A,B,C)) puts("true"); else puts("false"); } return 0; }
16. HDU 2175 汉诺塔IX ( 数学/ 递推 / hanoi问题)
这道题有人说是找规律-> 详见 。 我一开始做的时候并没有这么想,而是继续递推 后来发现这题还是可以递推的。 我昨晚写的代码可能有问题。 具体思路: 从n开始递减去找 (T = 2^n) 和 (m) 的关系 递归: 1. 如果 m < T n--, 继续递归 2. 如果 m = T 这个时候在草稿纸上画一画应该知道正好是移动了第n+1个盘子,结束递归 3. 如果 m > T m - T, 继续递归
#include <cstdio> unsigned __int64 m, bit[65] = {1}; int n; void init_bit() { for(int i=1;i<=64;i++) bit[i] = bit[i-1] << 1; } void judge(int n,unsigned __int64 x) { if(x < bit[n]) judge(n-1,x); else if(x == bit[n]) { printf("%d\n",n+1); return; } else judge(n,x-bit[n]); } int main() { init_bit(); while(~scanf("%d%I64d",&n,&m) && (m+n)) { judge(n,m); } }
#include <cstdio> __int64 m, bit[64] = {1}; int n; void init_bit() { for(int i=1;i<64;i++) bit[i] = bit[i-1] << 1; } void judge(int n,__int64 x) { if(x < bit[n-1]) judge(n-1,x); else if(x == bit[n-1]) { printf("%d\n",n); return; } else judge(n,x-bit[n-1]); } int main() { init_bit(); while(~scanf("%d%I64d",&n,&m) && (m+n)) { judge(n,m); } }
17. HDU 4907 Task schedule
18. HDU 4908 BestCoder Sequence (详见BC #3 )
19. HDU 2511 汉诺塔 X ( 数学/ 递推 / hanoi问题)
问第m次移动的是哪一个盘子,从哪根柱子移到哪根柱子.例如:n=3,m=2. 回答是 :2 1 2,即移动的是2号盘,从第1根柱子移动到第2根柱子 。 继续递归。模拟、
#include <cstdio> #define LL long long LL bit[65] = {1}, m; int n,t; void init_bit() { for(int i=1;i<64;i++) bit[i] = bit[i-1] << 1; } void judge(int a,int b,int c,int n,LL m) { if(n == 0) return; if(m > bit[n-1]) judge(b,a,c,n-1,m-bit[n-1]); else if(m == bit[n-1]) { printf("%d %d %d\n",n,a,c); return; } else judge(a,c,b,n-1,m); } int main() { init_bit(); scanf("%d",&t); while(t--) { scanf("%d %I64d",&n,&m); judge(1,2,3,n,m); } return 0; }
20. HDU 2184 汉诺塔VIII ( 数学/ 递推 / hanoi问题)
问移动m次后的状况.
还是递归。。
#include <cstdio> #include <cstring> #define LL long long LL bit[65] = {1}, m; int n, t, a[70], b[70], c[70]; void init_bit() { for(int i=1;i<64;i++) bit[i] = bit[i-1] << 1; } void judge(int* a,int* b,int* c,int n,LL m) { if(n == 0) return; if(m > bit[n-1]) { c[++c[0]] = n; judge(b,a,c,n-1,m-bit[n-1]); } else if(m == bit[n-1]) { c[++c[0]] = n; for(int i=1;i<n;i++) { b[++b[0]] = n - i; } } else { a[++a[0]] = n; judge(a,c,b,n-1,m); } } void solve() { scanf("%d %I64d",&n,&m); a[0] = b[0] = c[0] = 0; judge(a,b,c,n,m); printf("%d",a[0]); for(int i=1;i<=a[0];i++) printf(" %d",a[i]); putchar('\n'); printf("%d",b[0]); for(int i=1;i<=b[0];i++) printf(" %d",b[i]); putchar('\n'); printf("%d",c[0]); for(int i=1;i<=c[0];i++) printf(" %d",c[i]); putchar('\n'); } int main() { init_bit(); scanf("%d",&t); while(t--) { solve(); } }
21. Codeforces 454B. Little Pony and Sort by Shift ( 模拟 )
自己有那么一个思路,就是把序列再复制一份到末尾,然后从末尾往前扫,如果非递减序列的元素个数==n了,说明找到了这个序列,而且移动次数是最少的。。但是卡在了第六个点, 关键是测试数据还看不全,没办法了,不知道那里有问题。 别人的思路是:首先统计非递减序列的的变化次数。如果ct = 1,说明pos处前后各有一个非递减序列,这时候考虑x[pos] 和 x[1] 以及 x[n] 和 x[1] 的关系。 如果ct >= 2 不可能通过移动来达成非递减序列的条件。输出-1; 如果ct == 0 说明不需要移动已经是一个非递减序列了,直接输出 0
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; #define maxn 101000 #define clr(a,b) memset(a,b,sizeof(a)) int x[maxn], n; int main() { scanf("%d",&n); int ct = 0, pos = 0; for(int i=1;i<=n;i++) { scanf("%d",&x[i]); if(x[i] < x[i-1]) ct++, pos = i; } if(ct >= 2) puts("-1"); else if(ct == 0) puts("0"); else { if(x[pos] <= x[1] && x[n] <= x[1]) printf("%d\n",n-pos+1); else puts("-1"); } }
22. Codeforces 454A. Little Pony and Crystal Mine ( 吓尿题 )
看完样例不看题目你可能就已经吓尿了。。。
想起了刚刚学习C语言时候的打印菱形
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define maxn 101000 6 #define clr(a,b) memset(a,b,sizeof(a)) 7 8 int main() 9 { 10 int n; 11 scanf("%d",&n); 12 13 int t = n >> 1; 14 for(int i=0;i<t;i++) 15 { 16 for(int j=0;j<t-i;j++) putchar('*'); 17 for(int k=0;k<(i<<1)+1;k++) putchar('D'); 18 for(int j=0;j<t-i;j++) putchar('*'); 19 putchar('\n'); 20 } 21 for(int i=0;i<n;i++) putchar('D'); 22 putchar('\n'); 23 for(int i=t-1;i>=0;i--) 24 { 25 for(int j=0;j<t-i;j++) putchar('*'); 26 for(int k=0;k<(i<<1)+1;k++) putchar('D'); 27 for(int j=0;j<t-i;j++) putchar('*'); 28 putchar('\n'); 29 } 30 putchar('\n'); 31 return 0; 32 }
23. Codeforces 451B. Sort the Array ( 模拟题 )
这题的思路我觉得和那题非递增序列很想。
因为只能旋转一次。所以如果出现2次以上递减的情况,答案就是no了
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define maxn 101000 6 #define clr(a,b) memset(a,b,sizeof(a)) 7 int n, x[maxn]; 8 int main() 9 { 10 int cnt = 0, s = 0, e = 0, flag = 0; 11 scanf("%d",&n); 12 for(int i=1;i<=n;i++) 13 { 14 scanf("%d",&x[i]); 15 if(x[i] < x[i-1] && flag == 0) 16 { 17 flag = 1; 18 cnt++; 19 s = i-1; 20 e = i; 21 } 22 else if(x[i] < x[i-1] && flag == 1) 23 { 24 e = i; 25 if(x[i] < x[s-1]) 26 cnt++; 27 } 28 else if(x[i] > x[i-1]) 29 { 30 flag = 0; 31 if(x[i] < x[s]) cnt++; 32 } 33 } 34 if(cnt == 0 ) 35 { 36 puts("yes"); 37 printf("1 1\n"); 38 } 39 else if(cnt >= 2) puts("no"); 40 else 41 { 42 puts("yes"); 43 printf("%d %d\n",s,e); 44 } 45 }
另外一种思路: 将数组排下序,然后从前向后,从后向前寻找不同到位置,这段l~r是一定要旋转的,然后判断旋转后的符不符合递增。注意l>r的情况。 3点,数组排序,查找判断,已特判
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 5 using namespace std; 6 const int maxn = 1e5+5; 7 8 int n, arr[maxn], pos[maxn]; 9 10 bool judge (int l, int r) { 11 for (int i = 0; i + l <= r; i++) { 12 if (arr[l+i] != pos[r-i]) 13 return false; 14 } 15 return true; 16 } 17 18 int main () { 19 scanf("%d", &n); 20 for (int i = 0; i < n; i++) { 21 scanf("%d", &arr[i]); 22 pos[i] = arr[i]; 23 } 24 25 sort(pos, pos + n); 26 int l = 0, r = n-1; 27 while (l < n && pos[l] == arr[l]) l++; 28 while (r >= 0 && pos[r] == arr[r]) r--; 29 30 if (judge(l, r)) { 31 if (r < l) 32 l = r = 0; 33 printf("yes\n%d %d\n", l+1, r+1); 34 } else 35 printf("no\n"); 36 return 0; 37 }
24. Codeforces 451A. Game the Sticks ( 简单博弈 )
题意:给你n+m根筷子,将他们分别水平、垂直放置,形成n*m个节点。两个人轮流选择一个点,将穿过这个点的两根筷子拿走,谁可以逼迫对方率先无法继续操作,谁就获胜,问获胜的是先手还是后手。
仔细一想,确实是 每次选择一个交叉点,就会减少两根stick
col,row两个方向是较小的stick数,如果是奇数,显然A先手,所以最后一次总是A取得,
取完后就没有交叉点了。所以就是t = min(col,row), 如果t 为奇数, A赢,否则 M赢
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define ll long long #define inf 1000000000 using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n,m,ans; int main() { n=read();m=read(); int t=min(n,m); if(t&1)puts("Akshat"); else puts("Malvika"); return 0; }
template <class T> inline bool scan_d(T& ret) { char c, sgn; if(c == getchar(),c == EOF) return 0; while(c != '-' && (c < '0' && c > '9')) c = getchar(); sgn = (c == '-') ? -1 : 1; ret = (c == '-') ? 0 : (c - '0'); while(c = getchar(), c => '0' && c <= '9') ret += ret*10+(c - '0'); ret *= sgn; return 1; }
25. HDU 4847 Wow! Such Doge! ( 模拟,水题,比赛的时候我居然用了KMP )
记得比赛的时候看到题目这么长,根本不想看。
后来郏老大看完题目说可能是KMP,我二话不说就上去写那道题了。
当时那段时间对KMP走火入魔了,所以想都没想就写KMP了。
赛后发现都是水过,哪里用什么KMP。。。
但是我还是用KMP过了,嘿嘿
题意:给定文本,求有几个doge,不区分大小写
1 #include <cstdio> 2 #include <cstring> 3 4 int main() 5 { 6 char ch; 7 int cnt = 0; 8 int t = 0; 9 while(~scanf("%c",&ch)) 10 { 11 if(t == 0 && (ch == 'd' || ch == 'D')) 12 t++; 13 else if(t == 1 && (ch == 'o' || ch == 'O')) 14 t++; 15 else if(t == 2 && (ch == 'g' || ch == 'G')) 16 t++; 17 else if(t == 3 && (ch == 'e' || ch == 'E')) 18 cnt++, t = 0; 19 else 20 t = 0; 21 } 22 printf("%d\n",cnt); 23 return 0; 24 }
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define clr(a,b) memset(a,b,sizeof(a)) 6 7 int next[10]; 8 char T[1000]; 9 char P[10] = "doge"; 10 int Plen = strlen(P); 11 int Tlen, cnt; 12 13 int get_val() 14 { 15 clr(next,0); 16 next[0] = -1; 17 int j = 0, k = -1; 18 while(j < Plen) 19 { 20 if(k == -1 || P[j] == P[k]) 21 { 22 j++; 23 k++; 24 next[j] = k; 25 } 26 else 27 k = next[k]; 28 } 29 } 30 31 void KMP() 32 { 33 int j = 0, i = 0; 34 Tlen = strlen(T); 35 while(i < Tlen && j < Plen) 36 { 37 if(j == -1) 38 { 39 i++; 40 j++; 41 } 42 else if(T[i] == P[j] || T[i] == P[j]-('a'-'A') || T[i] == P[j]+('a'-'A')) 43 { 44 i++; 45 j++; 46 } 47 else 48 j = next[j]; 49 if(j == Plen) 50 { 51 cnt++; 52 j = 0; 53 } 54 } 55 } 56 57 int main() 58 { 59 // freopen("1.txt","r",stdin); 60 get_val(); 61 cnt = 0; 62 while(gets(T)) 63 { 64 KMP(); 65 } 66 printf("%d\n",cnt); 67 return 0; 68 }
26. CodeForces 445A DZY Loves Chessboard ( 模拟 )
题意:给一个二维数组,若数组中放的是‘-’,就不要改变,若是‘.’就要改成‘B’或‘W’,而且‘B’旁边不能再是‘B’,‘W’也一样。 自己想得一中办法是先从第一行开始,满足要求进行输出,然后第二行就根据第一行来输出。 这里我用了一个st,然后用的异或运算。。。实际上就是保证相邻的两个字符不能相同。(左右上下都是).记得好像1A了。。 另外一种,其实也和我想法差不多,但是很清晰。 直接预处理。。。然后如果是'-',就输出'-',其他就输出字符。 具体看代码,不用多说了。、
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 char G[110][110]; 6 char ch[3] = "WB"; 7 int main() 8 { 9 int n, m; 10 scanf("%d %d\n",&n,&m); 11 int st = 1; 12 for(int i=0;i<n;i++) 13 scanf("%s",&G[i]); 14 for(int j=0;j<m;j++) 15 { 16 if(G[0][j] != '-') 17 printf("%c",ch[st]); 18 else 19 putchar('-'); 20 st ^= 1; 21 } 22 puts(""); 23 for(int i=1;i<n;i++) 24 { 25 st = (i%2)^1; 26 for(int j=0;j<m;j++) 27 { 28 if(G[i][j] != '-') 29 { 30 if(G[i-1][j] == 'W') 31 putchar('B'); 32 else if(G[i-1][j] == 'B') 33 putchar('W'); 34 else 35 putchar(ch[st]); 36 } 37 else 38 putchar('-'); 39 st ^= 1; 40 } 41 puts(""); 42 } 43 44 return 0; 45 }
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 5 using namespace std; 6 const int maxn = 100; 7 8 int n, m; 9 char s[maxn+5][maxn+5]; 10 11 int main () { 12 13 scanf("%d%d", &n, &m); 14 for (int i = 0; i < n; i++) 15 scanf("%s", s[i]); 16 17 for (int i = 0; i < n; i++) { 18 for (int j = 0; j < m; j++) 19 if (s[i][j] == '.') { 20 printf("%c", (i+j)%2 ? 'W' : 'B'); 21 } else 22 printf("%c", s[i][j]); 23 printf("\n"); 24 } 25 return 0; 26 }
27. HDU 4772 Zhuge Liang's Password ( 模拟 )
连90°旋转都忘记怎么写了,。悲剧。。
这里写完90°旋转函数就可以了。
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; int A[110][110],B[110][110]; int T[110][110]; int n, ans; void rt() { int t = 0; for(int i=n-1;i>=0;i--) { for(int j=0;j<n;j++) { T[j][t] = A[i][j]; } t++; } for(int i=0;i<n;i++) for(int j=0;j<n;j++) A[i][j] = T[i][j]; } void input(int M[110][110]) { for(int i=0;i<n;i++) for(int j=0;j<n;j++) scanf("%d",&M[i][j]); } void judege() { int tmp = 0; for(int i=0;i<n;i++) for(int j=0;j<n;j++) if(A[i][j] == B[i][j]) tmp++; if(tmp > ans) ans = tmp; } int main() { while(~scanf("%d",&n) && n) { ans = 0; input(A); input(B); for(int i=0;i<4;i++) { if(i) rt(); judege(); } printf("%d\n",ans); } return 0; }
矩阵行列变换的核心公式是:map[i][j] = a[j][n-i-1]
28. Codeforces Round #253 A. Anton and Letters ( 模拟 )
集合元素统计,,用一个Hash就好了。。。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 6 int Hash[256]; 7 8 int main() 9 { 10 int cnt = 0; 11 char ch; 12 while(~scanf("%c",&ch)) 13 { 14 if(ch >='a' && ch <= 'z') 15 { 16 if(Hash[ch] == 0) 17 { 18 Hash[ch]++; 19 cnt++; 20 } 21 } 22 } 23 printf("%d\n",cnt);
29. CodeForces 439A Devu, the Singer and Churu, the Joker ( 模拟 )
这题没什么说的啊。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 6 7 int main() 8 { 9 int n, d; 10 scanf("%d %d",&n, &d); 11 int tol = 0, cnt = 0, t; 12 for(int i=0;i<n-1;i++) 13 { 14 scanf("%d",&t); 15 tol += t; 16 tol += 10; 17 cnt += 2; 18 } 19 scanf("%d",&t); 20 tol += t; 21 if(tol > d) printf("-1\n"); 22 else 23 { 24 cnt += (d - tol)/5; 25 printf("%d\n",cnt); 26 } 27 return 0; 28 }
30. CodeForces 250 A. The Child and Homework ( 模拟 )
这题也是水题。。没啥说的。。看懂题意。。。。
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 6 char a[110],b[110],c[100],d[110]; 7 int la,lb,lc,ld,cnt; 8 char res; 9 void judge(int a,int b,int c,int d,char ch) 10 { 11 int t = a << 1; 12 if(t <= b && t <= c && t <= d) 13 { 14 cnt++; 15 res = ch; 16 return; 17 } 18 t = a >> 1; 19 if(t >= b && t >= c && t >= d) 20 { 21 cnt++; 22 res = ch; 23 return; 24 } 25 } 26 27 int main() 28 { 29 scanf("A.%s B.%s C.%s D.%s",a,b,c,d); 30 la = strlen(a), lb = strlen(b), lc = strlen(c), ld = strlen(d); 31 cnt = 0; 32 judge(la,lb,lc,ld,'A'); 33 judge(lb,la,lc,ld,'B'); 34 judge(lc,lb,la,ld,'C'); 35 judge(ld,lb,lc,la,'D'); 36 if(cnt == 0 || cnt >= 2) puts("C"); 37 else printf("%c\n",res); 38 return 0; 39 }
31. CodeForces 432A Choosing Team ( 模拟 )
WF参加选队。。。。看懂题目果断1A
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 6 int main() 7 { 8 int n, k, cnt = 0; 9 int x[2020]; 10 scanf("%d %d",&n,&k); 11 for(int i=0;i<n;i++) 12 { 13 scanf("%d",&x[i]); 14 x[i] = 5 - x[i] - k; 15 if(x[i] >= 0) cnt++; 16 } 17 if(cnt >= 3) 18 { 19 printf("%d\n",cnt/3); 20 } 21 else puts("0"); 22 23 return 0; 24 }
32. CodeForces 432B Football Kit ( 模拟 )
这题TLE了很多次。。。 还是没能想出一个O(N)的算法。。 看了别人的解题报告知道了。。。 for(int i=0;i<n;i++) //统计主场衣服出现的次数 cnt[ x[i] ]++; for(int i=0;i<n;i++) { ans_home[i] = n - 1; //初始情况是n-1次主场,n-1次客场 ans_home[i] += cnt[ y[i] ];//y[i]为i队客场的球衣。有cnt[ y[i] ]个队主场也是穿这个球衣,所以这种情况,i队需要穿自己的主场球衣,所以 += cnt[ y[i] ] ans_away[i] = 2 * (n - 1) - ans_home[i];//再通过ans_home 算 ans_away }
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define maxn 101010 6 int cnt[maxn], n, x[maxn],y[maxn]; 7 int ans_home[maxn], ans_away[maxn]; 8 9 int main() 10 { 11 scanf("%d",&n); 12 for(int i=0;i<n;i++) 13 scanf("%d %d",&x[i],&y[i]); 14 for(int i=0;i<n;i++) 15 cnt[ x[i] ]++; 16 for(int i=0;i<n;i++) 17 { 18 ans_home[i] = n - 1; 19 ans_home[i] += cnt[ y[i] ]; 20 ans_away[i] = 2 * (n - 1) - ans_home[i]; 21 } 22 for(int i=0;i<n;i++) 23 printf("%d %d\n",ans_home[i],ans_away[i]); 24 return 0; 25 }
33. HDU 4802 GPA ( 模拟 )
果断很水的模拟题,,算绩点的,,
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <iostream> 5 #include <string> 6 using namespace std; 7 8 double judge(char s[]) 9 { 10 if(!strcmp(s,"A")) return 4.0; 11 else if(!strcmp(s,"A-")) return 3.7; 12 else if(!strcmp(s,"B+")) return 3.3; 13 else if(!strcmp(s,"B")) return 3.0; 14 else if(!strcmp(s,"B-")) return 2.7; 15 else if(!strcmp(s,"C+")) return 2.3; 16 else if(!strcmp(s,"C")) return 2.0; 17 else if(!strcmp(s,"C-")) return 1.7; 18 else if(!strcmp(s,"D")) return 1.3; 19 else if(!strcmp(s,"D-")) return 1.0; 20 else if(!strcmp(s,"F")) return 0.0; 21 } 22 23 int n,x,sco; 24 char op[3]; 25 double res; 26 27 int main() 28 { 29 while(~scanf("%d",&n)) 30 { 31 sco = res = 0; 32 for(int i=0;i<n;i++) 33 { 34 scanf("%d%s",&x,op); 35 if(op[0] == 'N' || op[0] == 'P') 36 continue; 37 else 38 { 39 sco += x; 40 res += x*judge(op); 41 } 42 } 43 if(res == 0 || sco == 0) puts("0.00"); 44 else 45 printf("%.2f\n",res = res/sco); 46 } 47 return 0; 48 }
34. HDU 4727 The Number Off of FFF ( 模拟 )
题目意思其实是,一个人报错了,后面的就跟着错。。。。
一直没搞清楚。。WA无数次、、、
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 6 int t, n, x[100100], res; 7 8 int main() 9 { 10 scanf("%d",&t); 11 for(int i=1;i<=t;i++) 12 { 13 scanf("%d",&n); 14 for(int j=1;j<=n;j++) 15 scanf("%d",&x[j]); 16 res = 1; 17 for(int i=2;i<=n;i++) 18 { 19 if(x[i] - x[i-1] != 1) 20 { 21 res = i; 22 break; 23 } 24 } 25 printf("Case #%d: %d\n",i,res); 26 } 27 return 0; 28 }
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 6 int t, n, x[100100], res; 7 8 int main() 9 { 10 scanf("%d",&t); 11 for(int i=1;i<=t;i++) 12 { 13 scanf("%d",&n); 14 for(int j=1;j<=n;j++) 15 scanf("%d",&x[j]); 16 17 res = 1; 18 for(int k=2;k<n;k++) 19 { 20 if( (x[k]-x[k-1] == 1) && (x[k+1] - x[k] != 1) ) 21 { 22 res = k + 1; 23 break; 24 } 25 else if( (x[k]-x[k-1] != 1) && (x[k+1] - x[k] == 1) ) 26 { 27 res = k - 1; 28 break; 29 } 30 else if( (x[k]-x[k-1] != 1) && (x[k+1] - x[k] != 1) ) 31 { 32 res = k; 33 break; 34 } 35 } 36 printf("Case #%d: %d\n",i,res); 37 } 38 return 0; 39 }
35.HDU 4716 A Computer Graphics Problem ( 模拟 )
计算机图形学问题??
巨水的一题
1 #include <cstdio> 2 3 int cas, x; 4 int main() 5 { 6 scanf("%d",&cas); 7 for(int i=1;i<=cas;i++) 8 { 9 scanf("%d",&x); 10 x = x/10; 11 printf("Case #%d:\n",i); 12 puts("*------------*"); 13 for(int j=0;j<10-x;j++) 14 puts("|............|"); 15 for(int j=0;j<x;j++) 16 puts("|------------|"); 17 puts("*------------*"); 18 } 19 }
36.HDU 4493 Tutor ( 模拟 )
这题简直坑爹。。。
才发现自己四舍五入没弄清楚。。。。。
.2f已经四舍五入了。。。。
这题就是处理后面两位。。到底有没有0。。。
1 #include <cstdio> 2 using namespace std; 3 4 int main() 5 { 6 int cas; 7 double x, sum; 8 scanf("%d",&cas); 9 while(cas--) 10 { 11 sum = 0; 12 for(int i=0;i<12;i++) 13 { 14 scanf("%lf",&x); 15 sum += x; 16 } 17 sum /= 12; 18 int t = (int)((sum+0.005)*100); 19 int a = t%10; 20 int b = t/10%10; 21 putchar('$'); 22 if(a == 0 && b == 0) 23 printf("%d\n",(int)sum); 24 else if(a == 0) 25 printf("%.1f\n",sum); 26 else 27 printf("%.2f\n",sum); 28 } 29 return 0; 30 }
1 #include <stdio.h> 2 #include <string.h> 3 4 int main() 5 { 6 int cas; 7 double x, sum; 8 scanf("%d",&cas); 9 while(cas--) 10 { 11 sum = 0; 12 for(int i=0;i<12;i++) 13 { 14 scanf("%lf",&x); 15 sum += x; 16 } 17 sum /= 12; 18 char str[100]; 19 sprintf(str,"$%.2f",sum); 20 int len = strlen(str); 21 if(str[len-1] == '0' && str[len-2] == '0') 22 str[len-3] = '\0'; 23 else if(str[len-1] == '0') 24 str[len-1] = '\0'; 25 printf("%s\n",str); 26 27 } 28 return 0; 29 }
sprintf(str,"$%.2f",sum); 学习这个用法。
37 - 44 详见 KMP总结