同质图，异质图，二部图，多元图等常见图的类型
文章目录
- 前言
- 一、常见图类型
- 二、Motif
- 同配性
- 轨道
- 常见模体
- 聚类系数
前言
传统的图数据分析通常采用监督学习的框架,即 通过人为特征提取或端到端图深度学习模型将图数据作为输入,经过训练后,挖掘图数据中的有效信息, 输出预测结果。虽然这类图监督学习方法在很多任务上取得了显著成功,但仍面临着以下问题:①依赖大量的人工标注数据;②由于过拟合导致泛化能 力差以及面向标签相关的攻击时模型鲁棒性差。 为了解决上述问题,不依赖于人工标注的自监 督学习正在成为图深度学习的趋势,其中,对比学习是一类重要的自监督学习方法.
对比学习是一种判别式的学习方法，其目的是让相似的样本学到相近的表示，同时让不相似样本的表示互相远离。
通常将图形式化成G={V,E},其中V={
,
,…,
}代表节点集合,E={
,
,…, 
}是边集合并且E⊆V×V。图的拓扑结构通常由邻接矩阵 A∈
表示其中
,当且仅当e=(vi,vj)∈ E,即节 点vi 和 节 点vj 之 间 存 在 一 条 连 边,否 则 Aij=0。
属性图是指那些节点关联着自身特征(也称为属性)的图。特征矩阵记做X ∈
,其 中, d 表示特征的维度, 第 i 行表示节点 v的特征，记做 
。
一、常见图的类型
上述的图（即前言中描述的图）：
- 只有一种节点类型和边类型，被称为同质信息图（同质信息网络）。
- 此外我们将那些具有不止一种类型的节点或者边的图记为异质信息图（异质信息网络）。
- 二部图是一种特殊的异质信息网络，其只有两种类型的节点，并且只有不同类型的节点之间存在连边。
- 多元图是另一种特殊的异质信息网络，它只包含一种类型的节点，但具有多种类型的连边。
- 时空图是一种特殊的属性图，它是指那些特征和结构随时间动态变化的图。其中第t个时间步的特征矩阵记为
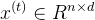，邻接矩阵为
。
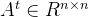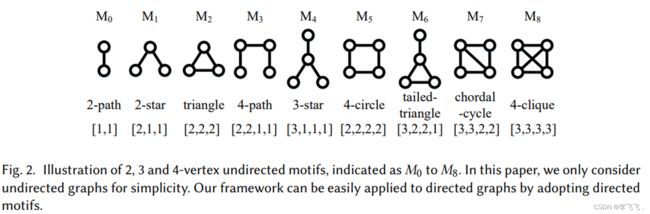
二、Motif
模体（Motif）是指在图中频繁出现的子图结构。（也被定义为满足一定条件时出现在真实网络中的诱导子图）
1，r（同配性）：用作考察度值相近的节点是否倾向于互相连接。
- 如果总体上度大的节点倾向于连接度大的节点，那么就称网络的度正相关的，或者称网络是同配的；
- 如果总体上度大的节点倾向于连接度小的节点，那么就称网络的度负相关的，或者称网络是异配的。
- 如果r>0，那么网络是同配的；如果r小于0，那么网络是异配的。
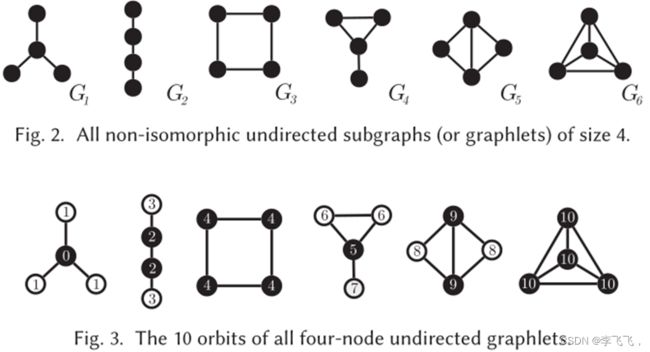
2. 轨道（Orbit)：
图自身的同构集称为自同构群：当存在一些将一个顶点映射到另一个顶点的自同构时，称两个顶点是等价的。这个等价关系将V（G）划分为等价类，我们称之为轨道。因此，轨道都是子图的唯一位置。例如，一个k-hub有k个节点，但只有两个轨道：一个中心轨道由单个节点占据，另一个叶轨道由其余k-1节点占据。同一轨道上的节点在拓扑上是等效的。图3显示了图2的所有不同轨迹。
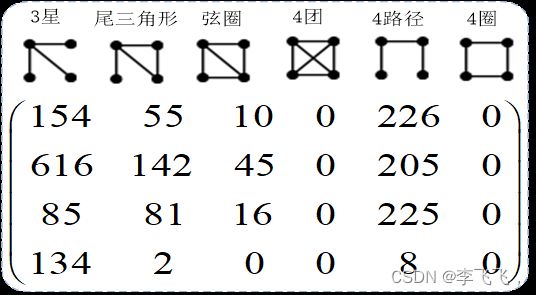
3.常见模体
图 1
4.聚类系数（Clustering coefficient）
在图论中，聚类系数是衡量图中节点倾向于聚类在一起的程度的指标. 聚类系数有两个版本：全局和局部。
（1）局部的聚类系数
- 一个顶点的局部聚类系数量化了它的邻居与团 clique（完全图）的接近程度。简单来说就是节点的一跳邻居内封闭三角形的比例（所以说三角形计数是聚类系数计算的基础）
- 个人倾向于该说法：一个节点的局部聚类系数体现的是其邻节点也相互连通的可能性。
举例说明：
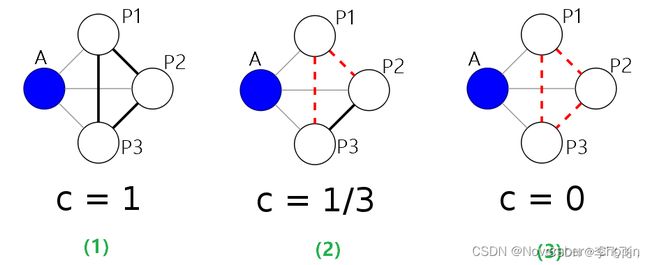图1 无向图上的局部聚类系数计算示例
图中的灰色线表示节点A与邻居的连接，黑实线是邻居之间的连接，红色表示图1(2)和(3)相比于图1(1)去掉的连接。
节点 A 的局部聚类系数计算为：其邻居之间实际实现的连接与所有可能连接的数量的比例，或者为节点A的一跳邻居内封闭的三角形的比例。(就是俩种计算方式，结果一致）
（2）全局的聚类系数 （待完善）
全局聚类系数是封闭三元组（或3个三角形）在三元组（开放和封闭）总数上的数量。
聚类系数参考自：图上的三角形计数和聚类系数 - 知乎 (zhihu.com)
图论中的聚类系数(Clustering coefficient)简单介绍_November丶Chopin的博客-CSDN博客
上述内容参考自：图对比的学习综述；保存的PPT