leetCode 647.回文子串 动态规划 + 优化空间 / 中心扩展法 + 双指针

647. 回文子串 - 力扣（LeetCode）

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。子字符串 是字符串中的由连续字符组成的一个序列。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

---

示例 1：

输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

---

>>思路和分析

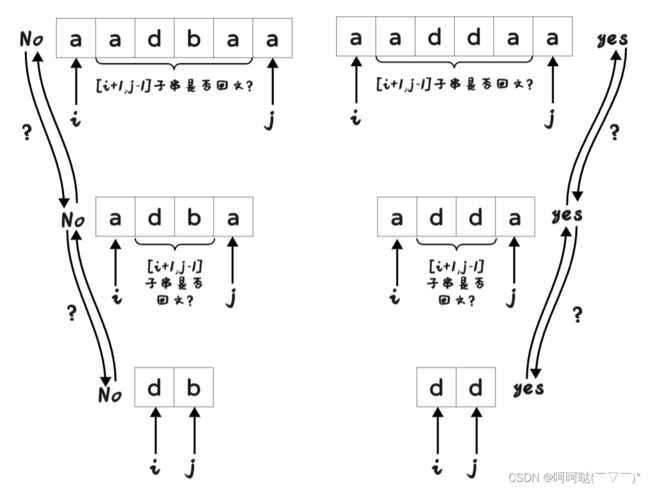
回文子串：讲究的是这个字符串里边左右两边是对称的，左右两边的元素是相同的。如果只判断这个字符串的最左面和最右面这两个元素相同的情况下，还知道中间的子串已经是回文的，那么就可以直接判断整个字符串它就是回文子串。

也就是说，如果在[i+1,j-1]范围的子串是一个回文串，再向两边拓展遍历的时候，那只需要判断两边这两个元素是否相同就可以了。若相同，dp[i][j]是回文串。

>>动规五部曲

1.确定dp数组以及下标的含义

• dp[i][j]:表示区间范围[i,j]的子串是否为回文子串。如果是，则dp[i][j] = true,否则为false

2.确定递推公式

当s[i] ≠ s[j]，肯定不是回文子串，那么 dp[i][j] = false;（由于dp[i][j]初始化为false，故此种情况不需要操作）

当s[i] == s[j]，分情况讨论： 

• 情况1：j - i > 1时，依赖 dp[i+1][j-1] = true

• 情况2：i = j,表指向同一个字符，例如 b ，此时 dp[i][j] = true,因为 b 是一个回文子串
• 情况3：j - i = 1; 例如 dd ,无法加入情况1讨论，因为无法依赖 dp[i+1][j-1] ，j-1=i,i+1=j,此时已经不满足dp数组中[i,j]闭区间这里的 j>=i 了。所以需要单独讨论。
  • 那 dd 这中情况在s[i] == s[j]下，也是回文子串，所以dp[i][j] = true

分析完三种情况，递推公式如下：

// result 用来统计回文子串的数量。
if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

3.dp 数组初始化

• dp[i][j]初始化为false

4.确定遍历顺序

一定要从下到上，从左到右遍历，这样能保证dp[i+1][j-1]是经过计算得来的

也可以是优先遍历列，然后遍历行，其实道理都一样，都是为了在使用dp[i+1][j-1]时能确保都经过计算了（可参考这篇文章：647. 回文子串 - 力扣（LeetCode））

5.举例推导dp数组

左边图是dp数组初始化，在填dp数组只会对右上三角进行数据更新，所以右边的图我就不画左下三角的0了。从图中，可得知有9个true，即有9个回文子串。还可以得知另一个信息，那就是回文子串有："a","b","d","d","b","a","dd","bddb","abddba"

注："dd"是回文子串的信息记录在(2,3)这个坐标，"bddb"是回文子串的信息记录在(1,4)这个坐标,"abddba"是回文子串的信息记录在(0,5)这个坐标，若为true，则该子串为回文。

(2,3),(1,4),(0,5)在左对角线上，所以观察的时候可以瞄准这条线上的坐标，分析信息

注：要明确和清晰dp[i][j] 表示区间范围[i,j]的子串是否为回文子串

• 左图的回文子串有："a","a","d","b","a","a","aa","aa"
• 右图的回文子串有："a","a","d","d","a","a","aa","dd","adda","aaddaa","aa"

（1）二维dp

class Solution {
public:
    int countSubstrings(string s) {
        vector> dp(s.size(), vector(s.size(), false));
        int result = 0;
        for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍历顺序
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    if (j - i <= 1) { // 情况一 和 情况二
                        result++;
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) { // 情况三
                        result++;
                        dp[i][j] = true;
                    }
                }
            }
        }
        return result;
    }
};

• 简洁写法：

class Solution {
public:
    int countSubstrings(string s) {
        vector> dp(s.size(), vector(s.size(), false));
        int result = 0;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
                    result++;
                    dp[i][j] = true;
                }
            }
        }
        return result;
    }
};

• 时间复杂度：O(n^2)
• 空间复杂度：O(n^2)

（2）二维dp 优化空间

class Solution {
public:
    int countSubstrings(string s) {
        vector> dp(2,vector(s.size(),false));
        int result = 0;
        for(int i=s.size()-1;i>=0;i--) {
            for(int j=i;j

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

（3）一维dp 优化空间

class Solution {
public: 
   int countSubstrings(string s) {
        vector dp(s.size(),false);
        int result = 0;
        for(int i=s.size()-1;i>=0;i--) {
            // int pre = dp[s.size()-1];
            bool pre = false;
            for(int j=i;j

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

---

>>其他解法：暴力解法 和 双指针

（1）暴力解法

• 两层循环，考察所有子串，判断是否是回文串

class Solution {
public:
    bool isPalindrome(string s) {
        int i = 0;
        int j = s.size()-1;
        while(i < j) {
            if(s[i] != s[j]) return false; 
            i++;
            j--;
        }
        return true;
    }
    // 时间复杂度:O(n^3)，空间复杂度:O(1)
    int countSubstrings(string s) {
        int count=0;
        // 两层循环，考察所有子串，判断是否是回文串
        for (int i = 0; i < s.size(); i++) {
            for (int j = i; j < s.size(); j++) {
                if (isPalindrome(s.substr(i, j + 1 - i))) count++;
            }
        }               
        return count;
    }
};

• 时间复杂度：O(n^3)
• 空间复杂度：O(1)

（2）双指针「中心扩展法」

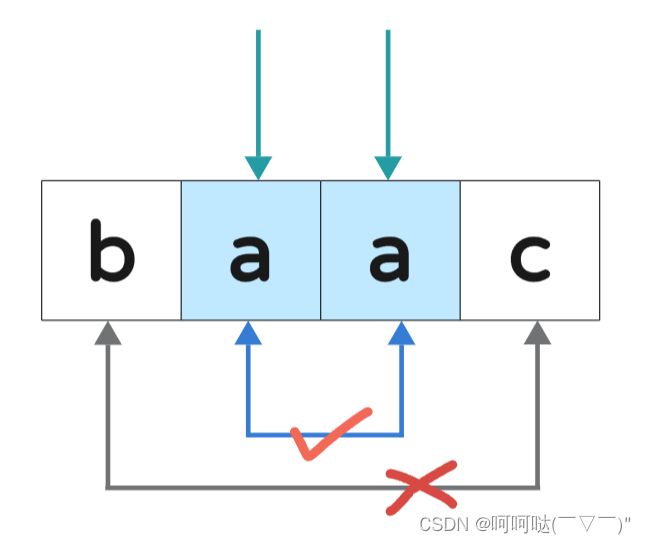
上文提到：回文字符串是关于中心对称的字符串，基于对称性的特点，可以采取向两边扩展的方法，得到回文子串

（1）以单个字符为中心（如果回文长度是奇数，那么回文中心是一个字符；）

上图字符串的中心是 c ，同时向左向右扩展一格，可以得到子串是 aca ，发现该扩展子串符合回文的性质。那么就继续向左向右扩展一格，得到子串 bacad ，不符合回文的性质，停止！

因此，以 c 为中心，可以得到的回文子串有两个： c 和 aca 

注：由于以单个字符为中心，会遗漏掉偶数回文子串的情况，故还有下文所讲的以两个字符为中心，一起来看看吧~

（2）以两个字符为中心（如果回文长度是偶数，那么中心是两个字符）

总结：「中心扩展法」的思想就是遍历以一个字符或两个字符为中心可得到的回文子串

---

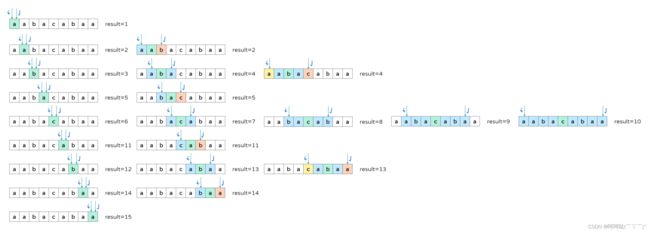
举个栗子：s = "aabacabaa"

• （1）以单个字符为中心（如果回文长度是奇数，那么回文中心是一个字符；）

• （2）以两个字符为中心（如果回文长度是偶数，那么中心是两个字符） 

故 result = 15 + 2 = 17 

class Solution {
public:
    int countSubstrings(string s) {
        int result = 0;
        for (int i = 0; i < s.size(); i++) {
            result += extend(s, i, i, s.size()); // 以i为中心（以单个字母为中心的情况）
            result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心（以两个字母为中心的情况）
        }
        return result;
    }
    int extend(const string& s, int i, int j, int n) {
        int res = 0;
        while (i >= 0 && j < n && s[i] == s[j]) {
            i--;
            j++;
            res++;
        }
        return res;
    }
};

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

拓展学习→中心点的个数：2 * len - 1

• aca 有 5 个中心点，分别是 a、c、a、ac、ca
• acca 有 7 个中心点，分别是 a、c、c、a、ac、cc、ca

参考和推荐文章、视频：

代码随想录 (programmercarl.com)https://www.programmercarl.com/0647.%E5%9B%9E%E6%96%87%E5%AD%90%E4%B8%B2.html#%E6%80%9D%E8%B7%AF

动态规划，字符串性质决定了DP数组的定义 | LeetCode：647.回文子串_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV17G4y1y7z9/?spm_id_from=pageDriver&vd_source=a934d7fc6f47698a29dac90a922ba5a3

647. 回文子串 - 力扣（LeetCode）https://leetcode.cn/problems/palindromic-substrings/solutions/380130/shou-hua-tu-jie-dong-tai-gui-hua-si-lu-by-hyj8/

647. 回文子串 - 力扣（LeetCode）https://leetcode.cn/problems/palindromic-substrings/solutions/1/liang-dao-hui-wen-zi-chuan-de-jie-fa-xiang-jie-zho/

来自代码随想录的课堂截图：

实战篇->我的下一篇文章： leetCode 5. 最长回文子串 动态规划 + 优化空间 / 中心扩展法 + 双指针-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133895681?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22133895681%22%2C%22source%22%3A%22weixin_41987016%22%7D