uva 658 It's not a Bug, it's a Feature!

原题：
Tinyware’s problem is a simple one. Given the original version of their software, which contains all
the bugs in B, it is possible to apply a sequence of patches to the software which results in a bug- free version of the software? And if so, assuming that every patch takes a certain time to apply, how long does the fastest sequence take?
Input
The input contains several product descriptions. Each description starts with a line containing two
integers n and m, the number of bugs and patches, respectively. These values satisfy 1 ≤ n ≤ 20 and 1 ≤ m ≤ 100. This is followed by m lines describing the m patches in order. Each line contains an integer, the time in seconds it takes to apply the patch, and two strings of n characters each.
The first of these strings describes the bugs that have to be present or absent before the patch can
be applied. The i-th position of that string is a ‘+’ if bug b i has to be present, a ‘-’ if bug b i has to be absent, and a ‘0’ if it doesn’t matter whether the bug is present or not.The second string describes which bugs are fixed and introduced by the patch. The i-th position of that string is a ‘+’ if bug b i is introduced by the patch, a ‘-’ if bug b i is removed by the patch (if it was
present), and a ‘0’ if bug b i is not affected by the patch (if it was present before, it still is, if it wasn’t,is still isn’t).
The input is terminated by a description starting with n = m = 0. This test case should not be
processed.
Output
For each product description first output the number of the product. Then output whether there is
a sequence of patches that removes all bugs from a product that has all n bugs. Note that in such a
sequence a patch may be used multiple times. If there is such a sequence, output the time taken by the fastest sequence in the format shown in the sample output. If there is no such sequence, output ‘Bugs cannot be fixed.’.Print a blank line after each test case.
Sample Input
3 3
1 000 00-
1 00- 0-+
2 0– -++
4 1
7 0-0+ —-
0 0
Sample Output
Product 1
Fastest sequence takes 8 seconds.
Product 2
Bugs cannot be fixed.
中文题意：
（这题真是太长了，而且还不太好读明白，前面一大堆废话！）
就是有一个软件公司，做了一个软件。现在要给这个软件打补丁，不过打补丁的过程有点说头。因为有的补丁要依赖于以前的bug，有的补丁会造成新的bug。现在给你两个数n和m，表示有n个固定的 bug，和m个补丁，接下来有m行，告诉给你补丁修复所需要的时间和两个字符串。第一个字符串是要想使用这个补丁你的状态必须是这个模样（减号代表此处没有bug，0代表无所谓，+号代码此处必须有bug），第二个字符串是你修复后的模样（0代码以前是什么现在就是什么样，-号代表此处bug已经修复，+代表此处bug又被搞出来了=_=)。最后问你能不能把bug全修好，如果能最少用多少时间？
数据量m的值为100n的值为20.

#include 
using namespace std;
const int STATE=1048577;
struct patch
{
    int cost;
    int before_m,before_a,after_m,after_a;
};
int n,m;
patch ps[101];
typedef pair<int,int> P;
int d[STATE];//2^20次幂个状态
bool used[STATE];

int dijkstra(int s,int t)
{
    priority_queuevector
,greater
 > que;
    memset(used,false,sizeof(used));
    fill(d ,d+t+1,INT_MAX);
    d[s]=0;
    que.push(P(0,s));
    while(!que.empty())
    {
        P p=que.top();
        que.pop();
        int v=p.second;
        if(d[v]continue;
        used[v]=true;
        for(int i=1;i<=m;i++)
        {
            patch pa=ps[i];
            if(((v&ps[i].before_m)==ps[i].before_m)&&(((~v)&ps[i].before_a)==ps[i].before_a))//判断能不能打补丁
            {
                int nv=v;
                nv|=(ps[i].after_m);//打上补丁
                nv&=(~ps[i].after_a);
                int cost=ps[i].cost;
                if(d[nv]>d[v]+cost)
                {
                    d[nv]=d[v]+cost;
                    que.push(P(d[nv],nv));
                }
            }
        }
    }
    return d[t];
}
int main()
{
    ios::sync_with_stdio(false);
    int k=0;
    while(cin>>n>>m,n+m)
    {
        int fin=(int)pow(2,n)-1;//1表示修复
        for(int i=1;i<=m;i++)
        {
            string before,after;
            cin>>ps[i].cost>>before>>after;
            ps[i].after_a=ps[i].after_m=ps[i].before_a=ps[i].before_m=0;
            for(int j=0;jif(before[j]=='-')//把减号和加号分开保存
                    ps[i].before_m|=(1<if(before[j]=='+')
                    ps[i].before_a|=(1<if(after[j]=='-')
                    ps[i].after_m|=(1<if(after[j]=='+')
                    ps[i].after_a|=(1<int ans=dijkstra(0,fin);//0表示bug
        cout<<"Product "<<++k<if(ans==INT_MAX)
            cout<<"Bugs cannot be fixed."<else
            cout<<"Fastest sequence takes "<" seconds."<cout<return 0;
}

超时的代码~其中使用了bitset

#include 
using namespace std;
const int STATE=1048577;
struct patch
{
    int cost;
    string before,after;
};
int n,m;
patch ps[101];
typedef pair<int,int> P;
int d[STATE];//2^20次幂个状态
bool used[STATE];
int apply(int sta,patch pa,int &new_v)
{
    bitset<20> bit=bitset<20>(sta);//bit的状态时反着的
    bitset<20> tmp(0);
    for(int i=0;iif(pa.before[i]=='-'&&bit[i]==0)
            return -1;
        if(pa.before[i]=='+'&&bit[i]==1)
            return -1;
        if(pa.after[i]=='0')
            tmp[i]=bit[i];
        else
        {
            if(pa.after[i]=='-')
                tmp[i]=1;
            else
                tmp[i]=0;
        }
    }
    new_v=(int)tmp.to_ulong();
    return pa.cost;
}
int dijkstra(int s,int t)
{
    priority_queuevector
,greater
 > que;
    memset(used,false,sizeof(used));
    fill(d ,d+t+1,INT_MAX);
    d[s]=0;
    que.push(P(0,s));
    while(!que.empty())
    {
        P p=que.top();
        que.pop();
        int v=p.second;
        if(d[v]continue;
        used[v]=true;
        for(int i=1;i<=m;i++)
        {
            patch pa=ps[i];
            int nv=0;
            int cost=apply(v,pa,nv);//nv表示打补丁以后的状态,返回值为花销
            if(cost==-1)//返回-1表示不能用该补丁
                continue;
            if(d[nv]>d[v]+cost)
            {
                d[nv]=d[v]+cost;
                que.push(P(d[nv],nv));
            }
        }
    }
    return d[t];
}
int main()
{
    ios::sync_with_stdio(false);
    int k=0;
    while(cin>>n>>m,n+m)
    {
        int fin=(int)pow(2,n)-1;//1表示修复
        for(int i=1;i<=m;i++)
            cin>>ps[i].cost>>ps[i].before>>ps[i].after;
        int ans=dijkstra(0,fin);//0表示bug
        cout<<"Product "<<++k<if(ans==INT_MAX)
            cout<<"Bugs cannot be fixed."<else
            cout<<"Fastest sequence takes "<" seconds."<cout<return 0;
}

解答：
刚看到这题的时候感觉好像动态规划，在纸上画了画图。图的样子是这样的，其中1,2,3分别表示1号，2号，3号补丁。x代表bug，v代表修复好了。

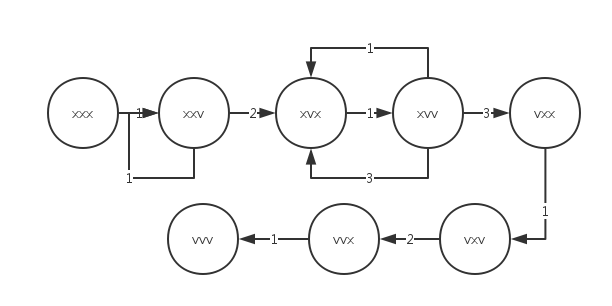
看到图和数据量后感觉应该是广搜或者是最短路径，考虑到节点的数量，使用可以优化dijkstra算法。其实在图里就能看出点小问题，一个bug要么是x要么是v那么可以用二进制状态压缩的方式来转移过程，不需要建立图，每次找到一个节点（这里应该成为状态），枚举m个补丁，判断当前的补丁能否使用，如果使用了，更新dijkstra当中记录路径长的数组即可。最后输出全是正确的状态是否满足。
这里我犯了个错误，考虑到数据量为2^(20)，大概是1000000，加上有100个补丁。dijkstra优化后的算法的时间复杂度是O(N*logM)其中M是节点数，N是边数。那么此题的时间复杂度如果按照每个状态在更新时采用遍历的方式判断是否能够打上补丁应该是N*logM*m*n，粗略的计算了一下，感觉没超过亿。结果交上去还是超时了，后来看了眼别人的代码，立刻就懂了=_=