数据库 索引结构B+树的伪代码
B+树一个很重要的特征就是:高度小。
深入学习B+树等索引相关数据结构 : 参考 MySQL索引背后的数据结构及算法原理
索引是搜索引擎去实现的 ;索引能极大的减少存储引擎需要扫描的数据量,索引可以把随机IO变成顺序IO。
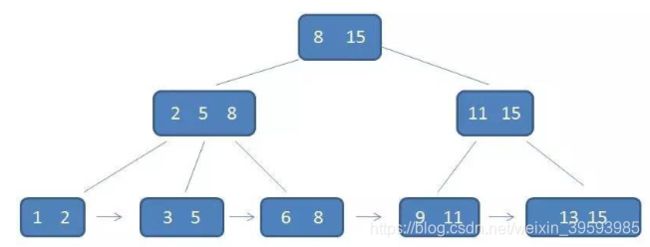
给出一个具体的M阶 B+树定义(《数据结构与算法分析》MAW著)
①数据项 只存储在树叶上。(数据项就是实实在在的数据,而不是索引)
②非叶子结点最多可以 存储 M个关键字(B树是M-1个)以指示搜索的方向(这里的关键字是指索引)。
这里的M个关键字是按从小到大的顺序排序的。M个关键字,就有M个指针,指向进一步查找的路径。
(有K个子节点就有K个索引,非叶子节点元素同时存在于叶子节点中,为其最大值或最小值)
这里表明,真正的数据只存储在叶子结点上。非叶子结点只存储索引(而不存储卫星数据,即索引元素所指向的数据记录,比如:数据库中的某一行,B+树中非叶子节点仅存在索引)。
需要补充的是,在数据库的聚集索引(Clustered Index)中,叶子节点直接包含卫星数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向卫星数据的指针。
在上面的具体规定中,M 和 L 是如何确定的呢?
M 和 L的确定与磁盘块的大小相关。对于B+树而言,每个结点都尽量占据一个磁盘块(也就是一页大小16K)。
参考 B-树(B+树) 学习总结
B+树索引伪代码一——搜索
搜索:
func find(<搜索码值> K) returns nodepointer //给定一个搜索码值,找出它的叶子节点 returns nodepointer 定义返回值类型
return tree-search(root, K); //从根开始搜索 返回 tree-search
end func
func tree-search(nodepointer, <搜索码值> K) returns nodepointer
//在树上搜索数据项
if nodepointer 是叶子结点,返回nodepointer
else
if K
if K≥Km, return tree-search(Pm, K); // M= 非叶子节点包含的关键字(索引)/目录项数 ,Pm对应最右端索引的子树 (i=M)
else
找到满足Ki≤K<Ki+1条件的i;// i取值1~M-1
return tree-search(Pi, K)
endfunc
B+树索引操作伪代码二——插入
插入:
proc insert(nodepointer, entry, newchildentry)
// 把entry插入到根为“*nodepointer”的子树中;
// “newchildentry”开始时是null,除非孩子被分裂,否则将已知返回null
if nodepointer IS非叶子节点,new NodeP N=nodepointer, //N对应的非叶子节点定长M
找到满足Ki≤entry的码值<Ki+1 条件的i; //选择子树
insert(Pi, entry, newchildentry); //递归插入entry 选择Pi子树 找到叶子节点插入entry
if newchildentry==null,return null; //通常的情况;不分裂孩子
else //需要分裂,必须在N中插入*nodepointer
//找到叶子结点添加后 NodeP newchildentry =
if N有空间, //通常情况
在N中放入*newchildentry ;
newchildentry=null,return null;//重新赋值为null
else //注意与叶子页分裂的差别
分裂N; //M个码值和M个节点指针
前M/2个码值和M/2个节点指针留下; // Old NodeP
后M/2个码值和M/2个节点指针移入到新节点N2中, // new NodeP
//*nodepointer 父节点 用于N和N2之间的搜索
newchildentry = &()
if N. isRoot,
分裂根节点,创建含有<指向N的指针,*nodepointer>的新节点;//新节点为<指向根节点N,N的值>
使树的根节点的指针指向新节点 //相当于复制了一份,作为子节点
return newchildentry;
if nodepointer IS叶子节点,new NodeP L=nodepointer, //大概 NodeP L = new NodeP(nodepointer);
if L有空间,//通常情况满足 L的大小为叶子节点可存储的数据项
在L中放入entry ,设newchildentry为null, 并返回;
else,//偶尔,叶子是满的 此时newchildentry
分裂叶子结点L成左右两个叶子结点:前L/2个数据项留于L,//Old NodeP
其余的移到新叶子节点L2中; //new NodeP
newchildentry = &(); //将第L/2+1个记录的K进位到父结点中
设置L和L2链接指针; //维护叶子结点之间的链表结构
return newchildentry;
endproc

 参考 B树和B+树的插入、删除图文详解 [赞!]
参考 B树和B+树的插入、删除图文详解 [赞!]
B+树索引操作伪代码三——删除
删除:
proc delete(parentpointer, nodepointer, entry, oldchildentry)
//把entry 从根为“nodepointer”的子树中删除;
//“oldchildentry”开始时是null,除非孩子被删除,否则将一直返回为null
if nodepointer 是非叶子节点,new NodeP N=nodepointer,
找到满足K i≤ entry 的关键值<K i+1条件的i //选择子树
delete(nodepointer, Pi, entry, oldchildentry); //递归删除 找到叶子结点
if oldchildentry ==null,return null; // 通常的情况,不删除孩子
else //删除孩子节点
从N中移出 oldchildentry, //接着,检查最小占用情况
if N中有剩余的目录项,//通常情况
oldchildentry=null,return null; //删除不再继续
else,//注意叶子页合并的差别
获得N的一个兄弟S;//利用parentpointer参数查找S
if S有多余的数据项,
通过父节点在N和S之间重新平均分布目录项;
oldchildentry=null,return;
else,合并N和S //称作合并的节点M
oldchildentry = &(父节点中指向M的当前目录项);
从父节点拉下分割码,并放在左侧节点上;
把M中的所有目录项移到左侧节点;
抛弃空节点M,return oldchildentry;
if nodepointer是叶子节点,new NodeP L=nodepointer
if L有剩余的目录项,//通常情况 L剩余数据项满足占有比率
移出entry; oldchildentry=null; return;
else, //偶尔,叶子的占有率过低
获得L的一个兄弟S;//利用父节点parentpointer 参数查找S
if S有多余的目录项
通过父节点在L和S之间重新平均分布目录项;
//考虑S为左兄弟节点, L找到父节点中的关键字修改,考虑S为有兄弟节点时,S找到父节点对应关键字修改
在父节点中找到指向右侧节点的目录项;//称为M S,L靠右的称为M
用M中新的最小码值代替父节点中的相应目录项中的码值;
oldchildentry=null,return;
else,合并L和S 成一个节点M //称作被合并的节点M
oldchildentry = & (父节点中指向M的当前数据项); //
把M中的所有数据项移到左侧节点; //数据项复制到 S,L中靠左的节点
抛弃空节点M,调整叶子结点之间的指针,return oldchildentry;//维护链表结构
endproc
//math.ceil(x)返回大于等于参数x的最小整数,即对浮点数向上取整.