JAVA基础（JAVA SE）学习笔记（二）变量与运算符

前言 

1. 学习视频：

尚硅谷Java零基础全套视频教程(宋红康2023版，java入门自学必备)_哔哩哔哩_bilibili

2023最新Java学习路线 - 哔哩哔哩

正文

第一阶段：Java基本语法

1. Java 语言概述

JAVA基础（JAVA SE）学习笔记（一）JAVA学习路线、行业了解、开发环境JDK17安装配置 和 JDK8同时配置-CSDN博客

1.6 注释

• 源文件中用于解释说明程序的文字，就是注释。
• 注释是一个程序员必须要具备的良好编程习惯。在实际开发中，程序员可以先将自己的思想通过注释整理出来，然后再用代码实现。

   

• 分为单行注释、多行注释、文档注释（Java特有）。

//单行注释

/*多行注释
         

 */

/**
  文档注释
  
  */

注释嵌套：
多行注释中可以嵌套单行注释，多行注释中不能嵌套多行注释。

• 编译后的字节码文件中不包含注释信息。

• 文档注释是对一段代码概括的解释说明，可以使用javadoc命令(java文件需要是public或protected)将文档注释提取出来生成帮助文档。生成一套以网页文件形式体现的该程序的说明文档。

      

javadoc -d mydir -author -version WenDangZhuShi.java

可以发现，除了class外部的文档注释和main方法外部的文档注释，其他注释都没有显示出来。

      

1.7 JAVA代码基本格式

1.7.1 java程序代码可以分为结构定义语句和功能执行语句：

•  结构定义语句：用于声明一个类或方法。
• 功能执行语句：用于实现具体功能。每条功能执行语句的最后都必须用分号（;）隔开。

1.7.2 严格区分大小写。

        User和user是两个完全不同的符号。

1.7.3 良好排版缩进。

        但也可以在两个单词或符号之间任意换行。

1.7.4 一句连续字符串不能分开在两行书写。要用+连接。

1.7.5 一个源文件中可以有多个类，但是最多只能有一个类声明为public，且要求声明为public的类的类名与源文件名相同。

1.8 Java API文档 （应用程序编程接口）

  

（API 在线查看）Overview (Java SE 17 & JDK 17)

（API 离线下载）Java Development Kit 17 Documentation

  

1.9 Java核心机制：JVM

  

  

功能：

• 实现java程序的跨平台性。（不同平台通过安装不同平台的java虚拟机）
• 自动内存管理（内存分配、回收）

   

内存溢出：程序（不是垃圾）过大，超出内存容量范围，就溢出，然后报错。

内存泄漏：垃圾不被JVM认为是垃圾，不会报错。

内存泄漏会导致内存溢出：内存泄漏的多，垃圾变多，且JVM不回收，超出内存容量，就溢出，然后报错。

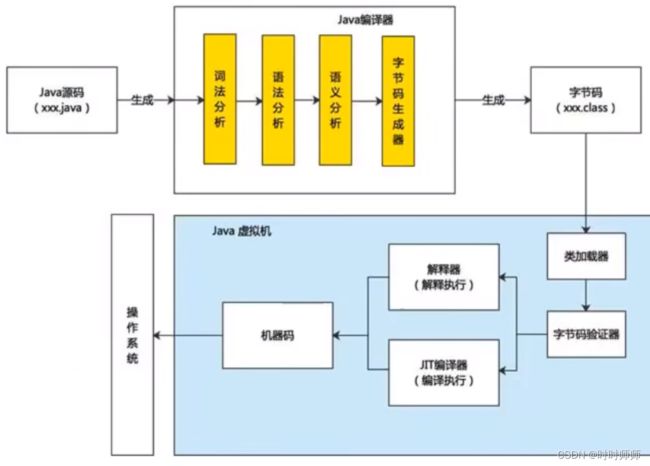
1.10 为什么java是半编译半解释型语言？

因为再java源文件被java编译器编译之后，生成的字节码文件在java虚拟机中有两种方式形成机器码，一种是通过解释器解释执行，另一种是通过JIT 即时编译器编译执行。

2. 变量与运算符

2.1 关键字 keyword

官方网址：Java Language Keywords (The Java™ Tutorials > Learning the Java Language > Language Basics) (oracle.com)

学习java语言 The Java™ Tutorials :(使用Microsoft Edgre 打开，可翻译可朗读，真是太友好了！感动！)Trail: Learning the Java Language (The Java™ Tutorials) (oracle.com)

定义：被Java 语言赋予了特殊含义，用做专门用途的字符串（单词）。
特点： 关键字中所有字母都为 小写。

2.2 标识符（identifier）

大驼峰：首字母都大写。

小驼峰：首单词小写，后面单词首字母大写。

2.3 变量 Variable

存储区域的每个内存单元都用一个标识符来标识。内存单元称为变量、定义的标识符称为变量名、内存单元存储的数据就是变量值。

2.3.1 变量的数据类型

java是一门强类型的编程语言，严格规定在定义变量时必须声明变量的类型，为变量赋值时必须赋予和变量同一种类型的值。否则会报错。java中的变量分为基本数据类型和引用数据类型两种。

8种基本数据类型是java语言内嵌的，在任何操作系统中都有相同大小和属性。

引用数据类型是由编程人员自己定义的变量类型。

8种基本数据类型： byte字节型、short短整型、int整型、long长整型

                                                    （超出int范围一定要加l或L。如long num = 198L）；

                       单精度浮点型float（必加f或F）、double双精度浮点型（可加、可不加d或D）；

                       字符型char；布尔型boolean。

6种引用数据类型：类class、接口interface、数组[]、枚举enum、注解annotation、记录record。

 原始数据类型（Java™ 教程> 学习Java语言>语言基础） (oracle.com)

2.3.2 作用域、范围、默认值

变量只在作用域{}内有效，出了作用域就失效了。

同一个作用域不能声明同名变量。

变量值不能超出变量类型的范围。

默认值：

2.3.3 float和double

变量赋值为 数学中用到的小数，分为单精度浮点数float（必须以F或f结尾，2e3f 、0f ）和双精度浮点数double（可以加或不加D或d结尾，3.84d、3.6d）。使用浮点数时不添加任何后缀，虚拟机会默认为double双精度浮点数。2e3f （e表示以10为底数的指数，-和+表示正负）表示2*10³且是单精度，即2000.0。

2.3.3.1 关于浮点型精度的说明

可以看出浮点型变量的精度不高，如果在开发中需要极高的精度，需要使用BigDecimal类。

几个小练习：

除不尽。

2.3.4  补充：计算机存储单位

2.3.5 char类型

字符类型的变量，用于存储一个单一的字符，要用英文半角格式的单引号''引起来，如'a'。每个char类型的变量占用2个字节。

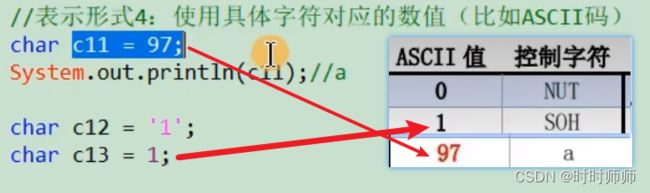
也可以将char类型的变量赋值为0~65535范围内的整数，计算机会自动将其转化为对应的字符，即ASCII转换。如'97'，打印结果是a。

char中赋值使用转义字符，代表的是ASCII的值。例如char ch1 = '\t';代表\t 制表符，相当于Tab键。

2.3.5.1 ASCII 编码、Unicode编码、UTF-8编码

ASCII代码_360百科

A——65，Z——90，a——97，z——122。0——48，9——57。

2.3.6 Boolean

2.3.7 基本数据类型变量的自动类型提升

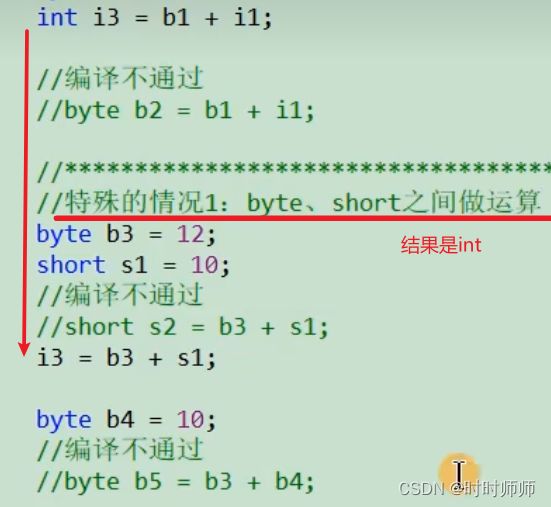
byte和short相加，结果是int。不是short。

认为'a'的ASCII转换的97是int类型。

最终结论：byte、short、char ——>int——>long——>float——>double

特别是byte、short、char之间的转换，结果都是int类型。

byte b1 = 3;
byte b2 = 4;
byte b3 = b1+b2; //报错,因为b1+b2时，b1和b2都被自动提升为int类型
//而int类型不能赋值给byte。
//正确写法
byte b3 = (byte)(b1+b2); 

float类型要加f或F，不然认为是double类型，就报错。

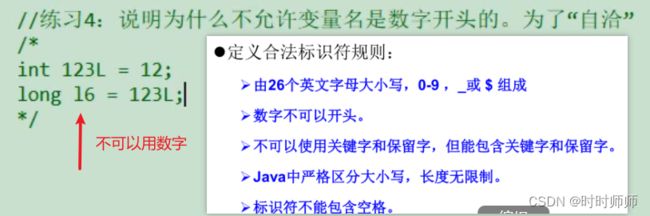
变量名虽然是标识符，但是不可以用数字，避免定义后赋值是数字。

2.3.8 基本数据类型变量的强制类型转换

最终结论：byte、short、char ——>int——>long——>float——>double

强制类型转换过程中可能导致数据溢出，进而出现错误结果。

在计算机中参与运算的数有两大类：无符号数和有符号数。

计算机中的数均存放在寄存器中，通常称寄存器的位数为机器字长。衡量机器字长的单位可用“位(bit)”。

无符号数：没有符号的数，在寄存器中的每一位均可用来存放数值。

有符号数：需要留出位置存放符号。

所以，机器字长为16位时，

        无符号数的表示范围为0~65 535，（65535=2的16次方-1）

        有符号数的表示范围为-32 768~+32767。（327 68=2的15次方）留一位为符号位

（那么byte表示范围为-128~127，128即2的7次方。）也要留一位为符号位。

都留了一位为符号位。

把符号“数字化”的数称为机器数，把带“-”和“+”符号的数称为真值。真值可以用二进制表示也可以用十进制表示。A=-26=（-11010）二进制

原码 = 符号位（0正或1负）+ 数值位（即真值的绝对值）。

约定整数：符号位与数值位之间用逗号隔开。约定小数：符号位与数值位之间用小数点隔开。

如“ +1110 为 0，1110 ”、“- 0.10101 为 1.10101”。

正数的原码、补码相同。

负数的原码求补码（求反加一）：看作原码除符号位外，每位求反，末位加一。

同样负数的补码求原码也是（求反加一）。

计算机的底层采用二进制补码存储。

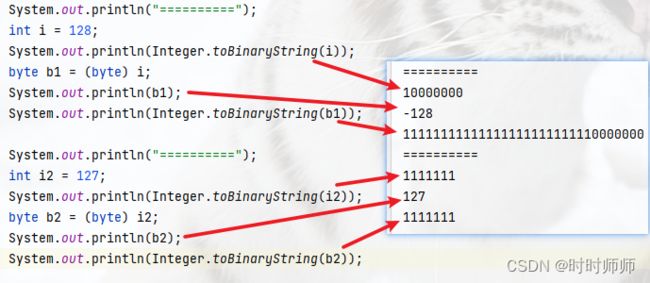
128是正数，int 32位，原码、反码、补码都是：

                        0（代表符号位，是正数）,000 0000 0000 0000 0000 0000 1000 0000。

128（int类型32位）在byte（8位）中存储时，补码只剩最后8位就是1000 0000。根据同样负数的补码求原码也是（求反加一）。1，000 0000除符号位外，每位求反得1，111 1111，末位加一后得1（溢出丢弃），1000 0000。最终得到：1000 0000，机器认为在byte中-128是1000 0000。

在byte中-128~+127的补码是：

1（代表符号位，是负数），000 0000   到  0（代表符号位，是正数）,111 1111。

所以计算机默认为int被byte强转后，在byte中1000 0000就是-128。所以输出结果是-128。

这里牵扯到：

1.byte占用8位，每位用0或1表示，能够表示256(2^8)个数据。

2.这8位分为符号位（最高位）和数值位（剩余七位），符号位0表示正数，1表示负数。

3.按上一步的理解，容易得到原码（+127：0111 1111、+1：0000 0001、+0：0000 0000、-0：1000 0000、-1：1000 0001、-127：1111 1111），计算机底层定义了+0（0000 0000）就是0，那么“可怜的-0”又该何去何从呢？计算机遇到这个二进制该如何处理呢？总不能把这两个都对应0吧，这显然是资源浪费。

4.到这里我们都认为最高位是不参与计算数值的，仅仅是一个符号位，按这种思路byte的八位是无论如何也表示不出-128。而“可怜的-0”又不知道自己代表谁，不得而知“可怜的-0”就是-128。（为什么呢？凭什么呢？你说代表-128就代表-128呀！为什么不能是+128、-250、+250.......）。

5.到这里我们已经很粗浅地回答了-128~127中的-128的由来，基本也回答了这个题目。

所以：
原码中 从1，111 1111到1，000 0001依次表示-127到-1。

补码中 从1，000 0001到1，111 1111依次表示-127到-1。

那么简单就认为计算机规定了1000 0000就是-128，是一种人为设计没有什么道理可以言（据说是印度阿三设计的）。其实这么设计也是很巧妙的，在于：
    【其一】对于如果大于8位的有符号整数数据类型，-128的补码尾八位刚好是1000 0000。
    【其二】比如127（补码0111 1111）加1（补码0000 0001）刚好得到-128（1000 0000），-128（补码1000 0000）加1（补码0000 00001）等于-127（补码1000 0001）这样从-128~127的反码首尾相连,形成了一个闭环，就像时钟一样。   
    【其三】在计算机中减法运算可以转换成加法运算，比如8-1——>8+(-1)——>补码运算：(0000 1000) + (1111 1111) = (0000 0111) 刚好是7。-128+127——>(1000 0000) + (0111 1111) = （1111 1111）刚好是-1，-128的补码完美的适用于减法。

结论：
    【1】计算机中负数是用补码的形式保存、并用它参与加减法运算的，减法会被转换为加法，计算机中没有减法运算。
    【2】反码是为了解决减法运算，补码是为了解决反码产生的±0的问题。参考(https://blog.csdn.net/boatalways/article/details/17027573)
    【3】对人而言二进制所代表的值一定是从原码求出的，开头如果是1的二进制，一定要说明其是原码、反码还是补码。
    【4】在原码、反码、补码相互转换以及求对应的十进制求值时，符号位是绝不参与的，但是在加减过程中，是参与位运算的。
    【5】计算机中规定了+0对应的二进制就是0，那么-0就没有意义了，必须找一个数和它对应。
    【6】byte的最小值-128、short的最小值-32768、int的最小值-2147483648都是用对应的-0的原码来进行表示，这是人为规定的、人为规定的、人为规定的。但是这么规定又很巧妙，妙在上述10中的三点。

在计算机中，这种超出机器字长的现象叫溢出。

-128是负数，8位中

原码：1（代表符号位，是负数），000 0000。

反码：1 ，111  1111。每位取反

补码：1，000 0000。末位加一

【-B】补 由 【B】补 连同符号位在内，每位取反，末位加一而得。

B=128是正数，int 32位，原码、反码、补码都是：0（代表符号位，是正数），000 0000 0000 0000 0000 0000 1000 0000。

-B=-128是负数，32位中，【-B】补 可得：

B=128补码：0（代表符号位，是负数），000 0000 0000 0000 0000 0000 1000 0000。

反码：1 ，111 1111 1111 1111 1111 1111 0111 1111。连同符号位在内，每位取反

补码：1， 111 1111 1111 1111 1111 1111 1000 0000。末位加一

2.4 常量 constant

常量就是在程序中固定不变的值，是不能改变的数据。

常量包括：整型常量、浮点常量、布尔常量、字符常量等。

• 整型常量：是int整数类型的数据，有二进制（必须以0b或0B开头，如0B011011）、八进制（必须0开头，如0711、0123）、十进制（第一位不能是0，0本身除外）、十六进制（必须0x或0X开头，如0x25AF）四种表示形式。
• 浮点常量：数学中用到的小数，分为单精度浮点数float（必须以F或f结尾，2e3f 、0f ）和双精度浮点数double（以D或d结尾，3.84d、3.6d）。使用浮点数时不添加任何后缀，虚拟机会默认为double双精度浮点数。2e3f （e表示以10为底数的指数，-和+表示正负）表示2*10³且是单精度，即2000.0。
• 字符常量：用于表示一个字符，要用英文半角格式的单引号''引起来。可以是英文字母、数字、标点符号以及转义序列（如 '\r' 、'\u0000' 空白字符）来表示的特殊符号。
• 字符串常量：一串连续的字符，要用英文半角格式的双引号""引起来。（可以包含一个或多个字符，也可以不包含任何字符，长度为零。）
• 布尔常量：只有true和false两个值。区分事物真假。
• null常量：只有一个null值，表示对象引用为空。

2.4.1 特殊字符——反斜杠（\）

在字符常量中，反斜杠是一个特殊字符，也称转义字符，作用是用来转义后面一个字符。转义后的字符通常用于表示一个不可见的字符或具有特殊含义的字符。如换行（\n）。下面是一些常见转义字符：

\r 回车，光标定位到这一行开头，不是下一行开头。

\n 换行符，光标定位到下一行开头

\t 制表符，相当于Tab键。

\b 退格符号，相当于backspace键。

\' 单引号字符。直接写'会认为两个是一对，会报错。

\" 双引号字符。如"  he says,\" thank you\".   "

\\ java中反斜杠是转义，所以要表示字面意义的反斜杠\，要使用两个反斜杠。

2.5 String类与8种基本数据类型变量间的运算，只能做连接运算，使用"+"表示。

String类，属于引用数据类型。赋值时需要使用一对双引号"",如 String str1 = "Hello World!";

String类声明的字符串内部，可以包含0个、一个、多个字符。

String类与8种基本数据类型变量间的运算，只能做连接运算，使用"+"表示。运算结果只能是String类型。不能转换为其他类型。

String转int可以使用Integer.parseInt()进行转换。如下：

几个例题：

下面这个注意啦：

大概是因为，42加9等于51，51代表的是3。

符号的十进制相加，再转成十进制对应的符号，输出是3。

证明：char类型输出的是ASCII的符号。

char类型，赋值时，单引号中是符号（包括转义符，如\t），输出就还是符号。

char类型，赋值时，值由 单引号中的符号进行 加号 运算，运算的过程中ASCII的符号对应的十进制数相加，输出十进制数相加的结果对应的符号。

而System.out.println('*'+'\t');打印的是ASCII的符号对应的十进制数相加。

2.6 进制转换

整型常量：是int整数类型的数据，有二进制（必须以0b或0B开头，如0B011011）、八进制（必须0开头，如0711、0123）、十进制（第一位不能是0，0本身除外）、十六进制（必须0x或0X开头，如0x25AF）四种表示形式。

2.6.1 二进制转十进制

《计算机组成原理》（唐朔飞 著）第6章P220~P225介绍：原码、反码、补码

在计算机中参与运算的数有两大类：无符号数和有符号数。

计算机中的数均存放在寄存器中，通常称寄存器的位数为机器字长。衡量机器字长的单位可用“位(bit)”。

无符号数：没有符号的数，在寄存器中的每一位均可用来存放数值。

有符号数：需要留出位置存放符号。

所以，机器字长为16位时，

        无符号数的表示范围为0~65 535，（65535=2的16次方-1）

        有符号数的表示范围为-32 768~+32767。（327 68=2的15次方）留一位为符号位

（那么byte，有8bit位，机器字长为8。表示范围为-128~127，即2的7次方。）也要留一位为符号位。

都留了一位为符号位。

把符号“数字化”的数称为机器数，把带“-”和“+”符号的数称为真值。真值可以用二进制表示也可以用十进制表示。

原码 = 符号位（0正或1负）+ 数值位（即真值的绝对值）。

约定整数：符号位与数值位之间用逗号隔开。约定小数：符号位与数值位之间用小数点隔开。

如“ +1110 为 0，1110 ”、“- 0.10101 为 1.10101”。

正数的原码、补码相同。

负数的原码求补码（求反加一）：看作原码除符号位外，每位求反，末位加一。

同样负数的补码求原码也是（求反加一）。

计算机的底层采用二进制补码存储。

在计算机中，这种超出机器字长的现象叫溢出。(

128是正数，int 32位，原码、反码、补码都是：

                        0（代表符号位，是正数）,000 0000 0000 0000 0000 0000 1000 0000。

128（int类型32位）在byte（8位）中存储时，补码只剩最后8位就是1000 0000。根据同样负数的补码求原码也是（求反加一）。1，000 0000除符号位外，每位求反得1，111 1111，末位加一后得1（溢出丢弃），1000 0000。最终得到：1000 0000，机器认为在byte中-128就是1，000 0000。

)

【-B】补 由 【B】补 连同符号位在内，每位取反，末位加一而得。

解释一下为什么：机器认为在byte中-128就是1，000 0000。

所以：
原码中 从1，111 1111到1，000 0001依次表示-127到-1。

补码中 从1，000 0001到1，111 1111依次表示-127到-1。

那么简单就认为计算机规定了1000 0000就是-128，是一种人为设计没有什么道理可以言（据说是印度阿三设计的）。其实这么设计也是很巧妙的，在于：
    【其一】对于如果大于8位的有符号整数数据类型，-128的补码尾八位刚好是1000 0000。
    【其二】比如127（补码0111 1111）加1（补码0000 0001）刚好得到-128（1000 0000），-128（补码1000 0000）加1（补码0000 00001）等于-127（补码1000 0001）这样从-128~127的反码首尾相连,形成了一个闭环，就像时钟一样。   
    【其三】在计算机中减法运算可以转换成加法运算，比如8-1——>8+(-1)——>补码运算：(0000 1000) + (1111 1111) = (0000 0111) 刚好是7。-128+127——>(1000 0000) + (0111 1111) = （1111 1111）刚好是-1，-128的补码完美的适用于减法。
详细解释：

1.byte占用8位，每位用0或1表示，能够表示256(2^8)个数据。

2.这8位分为符号位（最高位）和数值位（剩余七位），符号位0表示正数，1表示负数。

3.按上一步的理解，容易得到原码（+127：0111 1111、+1：0000 0001、+0：0000 0000、-0：1000 0000、-1：1000 0001、-127：1111 1111），计算机底层定义了+0（0000 0000）就是0，那么“可怜的-0”又该何去何从呢？计算机遇到这个二进制该如何处理呢？总不能把这两个都对应0吧，这显然是资源浪费。

4.到这里我们都认为最高位是不参与计算数值的，仅仅是一个符号位，按这种思路byte的八位是无论如何也表示不出-128。而“可怜的-0”又不知道自己代表谁，不得而知“可怜的-0”就是-128。（为什么呢？凭什么呢？你说代表-128就代表-128呀！为什么不能是+128、-250、+250.......）。

5.到这里我们已经很粗浅地回答了-128~127中的-128的由来，基本也回答了这个题目。

所以：

补码中 从10000001到11111111依次表示-127到-1。

那么简单就认为计算机规定了1000 0000就是-128，是一种人为设计没有什么道理可以言（据说是印度阿三设计的）。其实这么设计也是很巧妙的，在于：
    【其一】对于如果大于8位的有符号整数数据类型，-128的补码尾八位刚好是1000 0000。
【其二】比如127（补码0111 1111）加1（补码0000 0001）刚好得到-128（1000 0000），-128（补码1000 0000）加1（补码0000 00001）等于-127（补码1000 0001）这样从-128~127的反码首尾相连,形成了一个闭环，就像时钟一样。   
    【其三】在计算机中减法运算可以转换成加法运算，比如8-1——>8+(-1)——>补码运算：(0000 1000) + (1111 1111) = (0000 0111) 刚好是7。-128+127——>(1000 0000) + (0111 1111) = （1111 1111）刚好是-1，-128的补码完美的适用于减法。

结论：
    【1】计算机中负数是用补码的形式保存、并用它参与加减法运算的，减法会被转换为加法，计算机中没有减法运算。
    【2】反码是为了解决减法运算，补码是为了解决反码产生的±0的问题。参考(https://blog.csdn.net/boatalways/article/details/17027573)
    【3】对人而言二进制所代表的值一定是从原码求出的，开头如果是1的二进制，一定要说明其是原码、反码还是补码。
    【4】在原码、反码、补码相互转换以及求对应的十进制求值时，符号位是绝不参与的，但是在加减过程中，是参与位运算的。
    【5】计算机中规定了+0对应的二进制就是0，那么-0就没有意义了，必须找一个数和它对应。
    【6】byte的最小值-128、short的最小值-32768、int的最小值-2147483648都是用对应的-0的原码来进行表示，这是人为规定的、人为规定的、人为规定的。但是这么规定又很巧妙，妙在上述10中的三点。

2.6.2 十进制转二进制、八进制、十六进制（取余的逆）

除二、八、十六取余的逆。

2.6.3 二进制转八进制

将一个二进制数100101010转换为八进制：

1.将每三位分成一段，100 101 010

2.将每段的数值分别查表替换，得：

100——4

101——5

010——2

3.将替换结果进行组合，转换结果就是0452。（八进制以0开头）

2.6.4 二进制转十六进制

将一个二进制数100101010转换为十六进制：

1.将每四位分成一段，1 0010 1010

2.将每段的数值分别查表替换，得：

      1——1

0010——2

1010——A

3.将替换结果进行组合，转换结果就是0X12A。（十六进制以0x或0X开头）

2.7 运算符（Operator）

2.7.1 运算符简介

2.7.1.1 算术运算符 

i++与++i没有任何区别，字节码文件也一样。开发过程中也使用自增或自减，不会改变变量的数据类型。（short i = 2；i ++；）应避免写：（short i = 2；i = i + 1；）。i+1自动转int会报错，而强转short（i = (short)(i + 1)；）造成内存浪费。注意：

• 除法运算时，除数和被除数都是整数，得到的结果也是整数。如果有小数参与，得到的接过会是小数。（3500/1000*1000得到3000。（因为3500/1000得到3。）2.5/10得到0.25。）
• 进行取模（%）运算时结果正负取决于被取模的数的正负，而与模数无关。（（-5）%3 ）结果是-2。而5%（-3）结果是2。）

int m = 2;
m = m++;
//则m最终值是2。
//因为: 先赋值，得到m=2，赋值后再运算的结果没有被再次赋值。
//这里把m看成下面的j，就可以：
int j = 0;
int m = 2;
j = m++;//则j=2。

2.7.1.2 赋值运算符 

=、+=、-=、*=、/=、%=。在为变量赋值时，当两种类型彼此不兼容的，或者目标类型取值范围小于源类型时，常常需要强制类型转换。但是使用+=、-=、*=、/=、%=运算符赋值时，则不用，会自动完成转换。如下by1 += 5;是不会报错的。

以+=为例，x+=3即x=x+3。-=、*=、/=、%=也一样。

2.7.1.3 比较（关系）运算符 

2.7.1.4 逻辑运算符 

     与 &    ：进行运算时先左后右，符号两边都要运算。

短路与 &&：进行运算时先左后右，一旦左边为false，右边不再参与运算。

常使用在条件判断或者循环结构中。

2.7.1.5 位运算符 

位运算符是针对二进制数的每一位进行运算的符号，它是专门针对0和1进行操作的。

按位异或 ^（异1同0）。

左移<< ：将操作数的所有二进制位向左移动1位，运算时，右边空位补0。左边移走部分舍去。

右移>> ：将操作数的所有二进制位向右移动1位，运算时，左边空位根据原数的符号位补0（正）或1（负）。

无符号右移>>> ：将操作数的所有二进制位向右移动1位，运算时，左边空位补0。（不考虑正负）。

2.7.1.6 条件运算符

2.7.1.7 运算符的优先级（尽量使用括号来实现运算顺序，避免产生歧义）

企业真题