算法通关村第六关——二叉树的层次遍历经典问题(白银)
算法通关村第六关——二叉树的层次遍历经典问题(白银)
-
- 基本的层序遍历与交换
-
- 1. 二叉树的层序遍历
- 2. 二叉树的层序遍历2
- 3. 二叉树的锯齿形层序遍历
- 4. N 叉树的层序遍历
-
- 4.1 广度优先算法
- 4.2 深度优先算法
- 几个处理每层元素的题目
-
- 1. 在每个树行中找最大值
- 2. 二叉树的层平均值
- 3. 二叉树的右视图
- 4. 找树左下角的值
基本的层序遍历与交换
1. 二叉树的层序遍历
102. 二叉树的层序遍历
一个简单的二叉树示例:
3
/ \
9 20
/ \
15 7
输出的结果应该是:
[
[3],
[9,20],
[15,7]
]
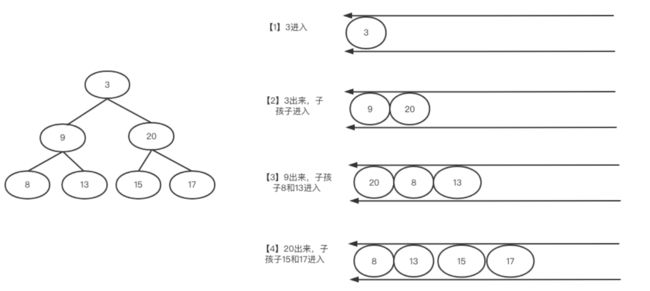
算法步骤如下:
- 创建一个空的结果集列表res和一个队列queue。
- 如果根节点不为空,则将根节点添加到队列中。
- 当队列不为空时循环执行以下操作:
- 获取当前队列的长度n,表示当前层级的节点数。
- 创建一个空的列表level,用于保存当前层级的节点值。
- 循环n次,每次从队列中取出一个节点进行处理。
- 将该节点的值添加到level列表中。
- 如果该节点的左子节点不为空,则将左子节点添加到队列中。
- 如果该节点的右子节点不为空,则将右子节点添加到队列中。
- 将level列表添加到结果集列表res中。
- 返回结果集列表res。
代码如下:
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if (root != null) {
queue.add(root);
}
while(!queue.isEmpty()){
List<Integer> level = new ArrayList<>();
int len = queue.size();
for(int i = 0; i<len; i++){
TreeNode node = queue.poll();
level.add(node.val);
if(node.left != null){
queue.add(node.left);
}
if(node.right != null){
queue.add(node.right);
}
}
res.add(level);
}
return res;
}
}
2. 二叉树的层序遍历2
107. 二叉树的层序遍历 II
一个简单的二叉树示例:
3
/ \
9 20
/ \
15 7
输出的结果应该是:
[
[15,7],
[9,20],
[3]
]
思路:
其实跟上面那题一样,我们只需要在添加进list的时候,添加到最前面即可,可以使用list.add(index,val)的方法,在索引为0的位置添加对应的值。
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new ArrayDeque<>();
if(root != null){
queue.add(root);
}
while(!queue.isEmpty()){
List<Integer> level = new ArrayList<>();
int len = queue.size();
for(int i=0; i<len; i++){
TreeNode node = queue.poll();
level.add(node.val);
TreeNode left = node.left, right = node.right;
if(left != null){
queue.add(left);
}
if(right != null){
queue.add(right);
}
}
res.add(0, level);
}
return res;
}
}
3. 二叉树的锯齿形层序遍历
leetcode 103. 二叉树的锯齿形层序遍历
一个简单的二叉树示例:
3
/ \
9 20
/ \
15 7
输出的结果应该是:
[
[3],
[20,9],
[15,76]
]
思路:
三个地方
- 判断左开始还是右开始,可以变成单数和偶数行,单数行左,偶数行右
- 双端队列可以前后添加数据和取出,那么,单数行添加就从后添加,这样就可以出现先进后出的感觉
- LinkedLIst的api,直接new LinkedList(双端队列),可以直接转换为集合。
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if(root == null){
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
Boolean isOrderLeft = true;
while(!queue.isEmpty()){
Deque<Integer> level = new LinkedList<Integer>();
int len = queue.size();
for(int i=0; i<len; i++){
TreeNode node = queue.poll();
if(isOrderLeft){
level.offerLast(node.val);
}else{
level.offerFirst(node.val);
}
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
res.add(new LinkedList<Integer>(level));
isOrderLeft = !isOrderLeft;
}
return res;
}
}
4. N 叉树的层序遍历
leeetcode 429. N 叉树的层序遍历
4.1 广度优先算法
这种方法跟前面的大差不差,就是主要是deque的处理
代码解释:
- 创建一个空的List
- res 用于存储最终结果。
- 创建一个空的双端队列Deque q,使用ArrayDeque实现,用于进行层次遍历。
- 如果根节点不为空,则将根节点添加到队列q中。
- 当队列q不为空时,执行循环体。
- 在每一层开始时,创建一个空的双端队列Deque next 和一个空的List nd,用于存储当前层的节点值。
- 在内层循环中,依次从队列q的队头取出节点cur,并将其值添加到nd中。
- 遍历cur的所有子节点chd,如果子节点不为空,则将其加入到next中。
- 内层循环结束后,将next赋值给q,以便继续遍历下一层。
- 将当前层的节点值列表nd添加到结果列表res中。
- 外层循环结束后,返回最终结果res。
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> res = new ArrayList<>();
Deque<Node> q = new ArrayDeque<>();
if(root != null){
q.add(root);
}
while(!q.isEmpty()){
Deque<Node> next = new ArrayDeque<>();
List<Integer> nd = new ArrayList<>();
while(!q.isEmpty()){
Node cur = q.pollFirst();
nd.add(cur.val);
for(Node chd : cur.children){
if(chd != null){
next.add(chd);
}
}
}
q = next;
res.add(nd);
}
return res;
}
}
使用广度优先搜索(BFS)算法实现N叉树的层次遍历的时间复杂度和空间复杂度如下:
- 时间复杂度:在最坏情况下,即当N叉树中的节点数为N时,我们需要访问所有的节点。对于每个节点,我们需要将其子节点加入队列,并在结果列表中添加该节点的值。因此,总体时间复杂度为O(N)。
- 空间复杂度:在进行BFS时,我们需要使用一个队列来存储当前层级的节点。在最坏情况下,即当N叉树是完全二叉树时,最多会有N/2个节点同时在队列中。因此,空间复杂度为O(N)。
4.2 深度优先算法
思路:
-
使用递归的方式进行深度优先搜索。在每次递归调用时,我们传入当前节点、当前层级和结果列表。如果当前层级超过了结果列表的大小,我们会在结果列表中添加一个新的空列表,用于存储当前层级的节点值。
-
然后,我们将当前节点的值添加到对应层级的列表中。接下来,我们对当前节点的所有子节点进行递归调用,将层级加一,并继续向下搜索。
-
最终,函数返回时,我们得到了一个按层级分组的节点值列表,即N叉树的层次遍历结果。
使用深度优先搜索(DFS)算法实现N叉树的层次遍历可以通过以下步骤来实现:
-
创建一个空的结果列表
res,用于存储最终的层次遍历结果。 -
如果根节点
root不为空,调用辅助函数dfs(root, 0, res)进行递归遍历。 -
在
dfs函数中,传入当前节点node、当前层级level和结果列表res。 -
如果当前层级
level大于等于结果列表res的大小,说明当前层级还没有被访问过,需要在结果列表中添加一个新的空列表。 -
将当前节点
node的值添加到结果列表res中对应层级的列表中。 -
遍历当前节点的所有子节点
child,如果子节点不为空,则进行递归调用dfs(child, level + 1, res),并将层级加一。 -
最终,函数返回时,我们得到了一个按层级分组的节点值列表,即N叉树的层次遍历结果。
下面是使用深度优先搜索算法实现N叉树层次遍历的Java代码示例:
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> res = new ArrayList<>();
if (root != null) {
dfs(root, 0, res);
}
return res;
}
private void dfs(Node node, int level, List<List<Integer>> res) {
if (level >= res.size()) {
res.add(new ArrayList<>());
}
res.get(level).add(node.val);
for (Node child : node.children) {
if (child != null) {
dfs(child, level + 1, res);
}
}
}
}
对于给定的N叉树,使用深度优先搜索(DFS)算法实现层次遍历的空间复杂度和时间复杂度如下:
- 空间复杂度:在递归的过程中,由于没有使用额外的数据结构来存储中间结果,所以空间复杂度是O(H),其中H是N叉树的高度。递归调用会在函数调用栈上占用一定空间,最坏情况下,当N叉树是一个单链表时,高度为N,因此空间复杂度为O(N)。
- 时间复杂度:在每个节点上,我们需要访问它的子节点,并且在结果列表中添加该节点的值。假设N叉树中的节点数为N,那么在最坏情况下,我们需要访问所有的节点,因此时间复杂度为O(N)。
几个处理每层元素的题目
1. 在每个树行中找最大值
leetcode 515. 在每个树行中找最大值
这题就比较简单啦~
其实就是层次遍历的变形,遍历节点的同时去判断值,那就需要拿一个值去获取,即可~
- 创建一个空的List res 用于存储每一层的最大值结果。
- 创建一个空的双端队列Deque q,使用ArrayDeque实现,用于进行层次遍历。
- 如果根节点不为空,则将根节点添加到队列q的尾部。
- 当队列q不为空时,执行循环体。
- 在每一层开始时,获取当前层的节点个数len,并初始化levelNumMax为最小整数值。
- 在内层循环中,依次从队列q中取出节点node,并更新当前层的最大值levelNumMax。
- 如果节点node有左子节点,则将其加入队列q的尾部。
- 如果节点node有右子节点,则将其加入队列q的尾部。
- 内层循环结束后,将当前层的最大值levelNumMax添加到结果列表res中。
- 外层循环结束后,返回最终结果res。
class Solution {
public List<Integer> largestValues(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> q = new ArrayDeque<>();
if(root != null){
q.addLast(root);
}
while(!q.isEmpty()){
int len = q.size();
int levelNumMax = Integer.MIN_VALUE;
for(int i=0; i<len; i++){
TreeNode node = q.poll();
levelNumMax = Math.max(node.val, levelNumMax);
if(node.left != null) q.addLast(node.left);
if(node.right != null) q.addLast(node.right);
}
res.add(levelNumMax);
}
return res;
}
}
2. 二叉树的层平均值
leetcode 637. 二叉树的层平均值
这题跟上一题一样的,只是把判断最大值改成计算总和,最后再添加到列表里,所以没什么好说的
class Solution {
public List<Double> averageOfLevels(TreeNode root) {
List<Double> res = new ArrayList<>();
Deque<TreeNode> q = new ArrayDeque<>();
if(root != null){
q.addLast(root);
}
while(!q.isEmpty()){
int len = q.size();
double sum = 0;
for(int i=0; i < len; i++){
TreeNode node = q.poll();
sum += node.val;
if(node.left != null) q.addLast(node.left);
if(node.right != null) q.addLast(node.right);
}
res.add(sum/len);
}
return res;
}
}
3. 二叉树的右视图
leetcode 199. 二叉树的右视图
这题也很简单,主要的难点是将节点放入队列后,怎样让弹出的节点是最右边那个
我直接用双端队列,比较简单,偷懒了~~不过,好像区别不大。
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> q = new ArrayDeque<>();
if (root != null) {
q.addLast(root);
}
while (!q.isEmpty()) {
int len = q.size();
int rightNode = 0;
for (int i = 0; i < len; i++) {
TreeNode node = q.poll();
rightNode = node.val; // 每一层的最右节点值更新为当前节点的值
if (node.left != null) {
q.addLast(node.left); // 将下一层的左子节点加入队列
}
if (node.right != null) {
q.addLast(node.right); // 将下一层的右子节点加入队列
}
}
res.add(rightNode); // 将每一层的最右节点值添加到结果列表
}
return res;
}
}
注意:
在每次遍历的过程中,通过不断取出队列中的节点,并更新rightNode变量为当前节点的值,可以保证q.poll()取出的是每一层的最右节点。
4. 找树左下角的值
leetcode LCR 045. 找树左下角的值
这题也差不多,也是在广度优先搜索的情况下多一点要求
这里找到最左的节点,也就是最下面那一层,遍历的时候,第一次遍历的第一个结点,那么也就是内嵌循环的第一次就是最左节点
class Solution {
public int findBottomLeftValue(TreeNode root) {
Deque<TreeNode> q = new ArrayDeque<>();
int leftValue = 0;
if (root != null) {
q.add(root); // 将根节点添加到队列中
}
while (!q.isEmpty()) {
int len = q.size();
for (int i = 0; i < len; i++) {
TreeNode node = q.poll();
if (i == 0) {
leftValue = node.val;
}
if (node.left != null) {
q.add(node.left);
}
if (node.right != null) {
q.add(node.right);
}
}
}
return leftValue;
}
}
搞定~~