Nested loop（PostgreSQL 14 Internals翻译版）

连接类型和方法

连接是SQL语言的一个关键特性;它们是其力量和灵活性的基础。行集(要么直接从表中检索，要么作为某些其他操作的结果接收)总是成对连接。

有几种类型的连接：

• 内连接。 内连接(指定为“INNER JOIN”或简称为“JOIN”)由满足特定连接条件的两个集合的行对组成。连接条件将一组行的一些列与另一组行的一些列结合起来；所有涉及的列都构成连接键。
  如果连接条件要求两个集合的连接键相等，这样的连接称为等连接（equi-join） ；这是最常见的连接类型。
  两个集合的笛卡尔积（CROSS JOIN） 包含了这些集合的所有可能的行对——它是具有真条件的内连接的一种特殊情况。

• 外连接。 左外部连接(指定为“LEFT OUTER”或简称“LEFT JION”)通过左集中没有与右集中匹配的行(相应的右侧列填充为NULL值)扩展内部连接的结果。
  对于右连接(RIGHT JOIN)也是如此，直到集合的排列。
  完整的外部连接(指定为FULL JOIN)包括左外部连接和右外部连接，添加没有找到匹配的右侧和左侧行。

• 反连接(ANTI-JOIN)及半连接(SEMI-JOIN)。 半连接看起来很像内部连接，但它只包括左集中与右集中有匹配的行(即使有几个匹配，也只包括一行)。
  反连接包括一个集合中在另一个集合中没有匹配的行。
  SQL语言没有显式的半连接和反连接，但是使用像“EXISTS”和“NOT EXISTS”这样的谓词也可以达到同样的结果。

所有这些连接都是逻辑操作。例如，内部连接通常被描述为已经清除了不满足连接条件的行的笛卡尔积。但是在物理级别上，内连接通常是通过成本较低的方式实现的。

PostgreSQL提供几种连接方法：

• nested loop join
• hash join
• merge join

连接方法是实现SQL连接的逻辑操作的算法。这些基本算法通常具有为特定连接类型量身定制的特殊风格，即使它们可能只支持其中的一些。例如，嵌套循环支持内部连接(在计划中由嵌套循环节点表示)和左外部连接(由嵌套循环左连接节点表示)，但它不能用于完全连接。
相同算法的某些风格也可以用于其他操作，例如聚合。
不同的连接方式在不同的条件下表现最佳；优化器的工作是选择最具成本效益的一种。

嵌套循环连接（Nested loop Joins）

嵌套循环连接函数的基本算法如下：外部循环遍历第一个集合(称为外部集合)的所有行。对于这些行中的每一行，将遍历第二组(称为内部集合)的行，以查找满足连接条件的行。 每个找到的对都会作为查询结果的一部分立即返回。
该算法访问内部集合的次数与外部集合的行数相同。因此，嵌套循环连接的效率取决于以下几个因素:

• 行外部集合的基数
• 可用的访问方法，可以有效地获取内部集所需的行
• 循环访问内部集合的同一行

笛卡尔积

不管集合中有多少行，嵌套循环连接是找到笛卡尔积的最有效方法:

嵌套循环节点使用上述算法执行连接。它总是有两个子节点：在计划中显示较高的一个对应于外部行集，而较低的一个代表内部行集。

在本例中，内部集合由Materialize节点表示。该节点返回从其子节点接收到的行，并保存它们以备将来使用(这些行在内存中累积，直到它们的总大小达到work_mem；然后PostgreSQL开始将它们溢出到磁盘上的临时文件中)。如果再次访问，该节点将读取累积的行，而不调用子节点。因此，执行器可以避免再次扫描整个表，而只读取满足条件的行。

类似的计划也可以用于使用常规对等连接的查询:

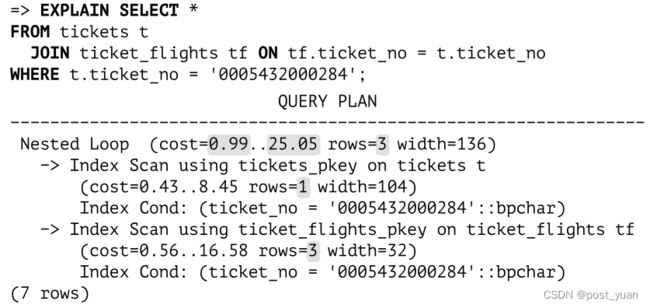
识别出两个值相等后，规划器将替换连接条件tf.ticket_no = t.ticket_no为t.ticket_no = constant条件，实际上将相等连接简化为笛卡尔积。

基数预估

笛卡尔积的基数估计为连接数据集的基数的乘积:3 = 1 × 3。

成本预估

连接操作的启动成本组合了所有子节点的启动成本。

连接的全部成本包括以下部分:

• 获取外部集合中所有行的成本
• 内部集合中所有行的单次检索的成本(因为外部集合的基数估计等于1)
• 处理要返回的每一行的成本

以下是成本估算的依赖关系图：

连接的开销计算如下：

现在让我们回到前面的例子：

该计划现在包含Materialize节点；一旦积累了从子节点接收到的行，Materialize就可以更快地为所有后续调用返回它们。

一般来说，连接的总成本包括以下费用：

• 获取外部集合中所有行的成本
• 内部集合中所有行的初始提取的成本(在此期间执行物化)
• (N−1)内部集合的行重复获取的代价(这里N是外部集合的行数)
• 处理要返回的每一行的成本

这里的依赖关系图如下：

在本例中，物化减少了重复数据获取的成本。计划中显示了第一次Materialize调用的成本，但没有列出所有后续调用的成本。我不会在这里提供任何计算，但在这个特殊的情况下，估计是0.0125。

因此，本例中执行的连接的成本计算如下:

参数化的连接

现在让我们考虑一个更常见的例子，它不能归结为笛卡尔积：

这里，Nested Loop节点遍历外层集合(tickets)的行，并对每一行搜索内部集合(ticket_flights)的对应行，将机票号(t.t ticket_no)作为参数传递给条件。当调用内部节点(Index Scan)时，它必须处理条件ticket_no = constant。

基数预估

规划器估计预订号的过滤条件由外部集合的两行(rows=2)满足，并且这些行平均每一行匹配内部集合的三行(rows=3)。

连接选择性是连接后剩下的两个集合的笛卡尔积的一个分数。显然，我们必须排除两个集合中在连接键中包含NULL值的行，因为它们永远不会满足相等条件。

估计的基数等于笛卡尔积的基数(即两个集合的基数的乘积)乘以选择性。

这里，第一个(外部)集合的估计基数是两行。由于除了连接条件本身之外，没有任何条件应用于第二个(内部)集，因此将第二个集的基数作为ticket_flights表的基数。

由于连接的表是通过外键连接的，因此选择性估计依赖于子表的每一行在父表中恰好有一个匹配行的事实。因此，选择性被视为外键所引用的表大小的倒数。

因此，对于ticket_no列中不包含NULL值的情况，估计如下：

显然，不使用外键也可以连接表。然后将选择性作为特定连接条件的估计选择性。

对于本例中的等连接，假设值均匀分布的选择性估计的一般公式如下：min(1/nd1,1/nd2)。

对不同值的统计表明票号表中的票号是唯一的
(这是意料之中的，因为ticket_no列是主键)，并且ticket_flights对于每张机票有大约三行匹配：

结果将与外键连接的估计相匹配：

优化器尽可能地改进这个基线估计。它目前不能使用直方图，但如果在两个表的连接键上收集了此类统计信息，它会考虑MCV列表。可以更准确地估计列表中出现的行的选择性，只有剩下的行必须依赖基于均匀分布的计算。

一般来说，如果定义了外键，连接选择性估计可能会更准确。对于复合连接键尤其如此，因为在这种情况下，选择性通常被大大低估了。

使用EXPLAIN ANALYZE命令，您不仅可以查看实际的行数，还可以查看内循环执行的次数:

外部集包含两行(actual rows=2);估计是正确的。因此，IndexScan节点执行了两次(loops=2)，每次它平均选择4行(actual rows=4)。因此，找到的行的总数:actual rows=8。

成本预估

这里的成本估算公式与前面的示例相同。

让我们回顾一下我们的查询计划：

在这种情况下，内部集合的每次后续扫描的代价与第一次扫描的代价相同。因此，我们最终得到以下数字：

缓存行

如果使用相同的参数值重复扫描内部集合(从而得到相同的结果)，那么缓存该集合的行可能是有益的。

这种缓存由Memoize节点执行。与Materialize节点类似，它被设计用于处理参数化连接，并且具有更复杂的实现：

• Materialize节点只是物化其子节点返回的所有行，而Memoize确保为不同参数值返回的行是分开保存的。
• 在溢出事件中，Materialize存储开始将行溢出到磁盘，而Memoize将所有行保留在内存中(否则缓存就没有意义了)。

下面是一个使用Memoize的查询示例：

用于存储缓存行的内存块的大小等于work_mem × hash_mem_multiplier 。正如第二个参数名称所暗示的那样，缓存的行存储在散列表中(使用开放寻址)。散列键(在计划中显示为Cache key)是参数值(如果有多个参数，则为多个值)。

所有的哈希键都绑定到一个列表中；它的一端被认为是冷的(因为它包含了很长时间没有使用的键)，而另一端是热的(它存储了最近使用的键)。

如果对Memoize节点的调用显示传递的参数值与已经缓存的行对应，则这些行将被传递到父节点(Nested Loop)，而不检查子节点。然后将使用的散列键移动到列表的热端。

如果缓存不包含所需的行，Memoize节点将从它的子节点提取这些行，缓存它们，并将它们传递给上面的节点。相应的哈希键也会变热。

在缓存新数据时，它会填满所有可用内存。为了释放一些空间，与冷键对应的行会被移除。这种驱逐算法不同于缓冲缓存中使用的算法，但目的相同。

一些参数值可能有太多匹配的行，以至于它们无法放入分配的内存块中，即使所有其他行都已经被清除。这些参数将被跳过——只缓存一些行是没有意义的，因为下一次调用仍然必须从子节点获取所有行。

成本及基数预估

这些计算与我们在上面看到的非常相似。我们只需要记住，计划中显示的Memoize节点的成本与其实际成本无关：它只是其子节点的成本增加了0.01的cpu_tuple_cost值。

对于Materialize节点，我们已经遇到了类似的情况：它的成本仅为后续扫描计算，而没有反映在计划中。

显然，只有当Memoize比它的子节点便宜时才有意义。每次后续Memoize扫描的成本取决于预期的缓存访问配置文件和可用于缓存的内存块的大小。计算值高度依赖于对内部行集扫描中使用的不同参数值数量的准确估计。基于这个数字，您可以权衡要缓存的行和要从缓存中删除的行的概率。预期的打击减少了估计成本，而潜在的驱逐增加了估计成本。我们将在这里跳过这些计算的细节。

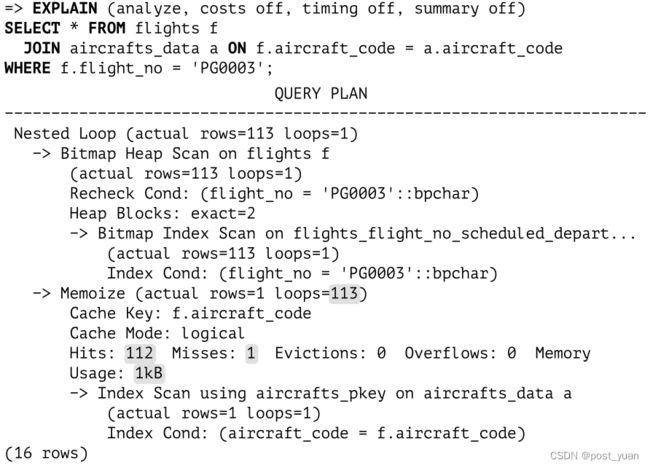
要弄清楚查询执行期间实际发生了什么，我们将使用EXPLAIN ANALYZE命令，像往常一样：

该查询选择遵循相同路线并由特定类型的飞机执行的航班，因此Memoize节点上的所有调用都使用相同的散列键。第一行必须从表中取出(Misses:1)，但所有后续行都在缓存中找到(Hits:112)。整个操作只需要1 KB的内存。

另外两个显示的值为零:它们表示在不可能缓存与一组特定参数相关的所有行时，清除的次数和缓存溢出的次数。较大的数字表明分配的缓存太小，这可能是由于对不同参数值的数量估计不准确造成的。那么Memoize节点的使用可能会非常昂贵。在极端情况下，可以通过关闭enable_memoize参数来禁止计划器使用缓存。

外连接

嵌套循环连接可用于执行左外连接：

这里的连接操作由嵌套循环左连接节点表示。规划器选择了一个带有过滤器的非参数化连接：它对内部行集执行相同的扫描(因此该集隐藏在Materialize节点后面)，并返回满足过滤器条件的行(join filter)。

外部连接的基数估计与内部连接的基数估计一样，不同之处在于计算的估计将与外部行集的基数进行比较，并采用较大的值作为最终结果。换句话说，外部连接永远不会减少(但可以增加)行数。

成本估算与内连接类似。

我们还必须记住，规划器可以为内连接和外连接选择不同的规划。即使是这个简单的例子，如果计划器被迫使用嵌套循环连接，也会有一个不同的Join Filter：

总成本的一个细微差别是由于外部连接还必须检查票号，以便在外部行的集合中没有匹配时获得正确的结果。

右连接不支持，因为嵌套循环算法对内部集和外部集的处理方式不同。外部集被完整扫描；至于内部集合，索引访问只允许读取满足连接条件的行，因此可以完全跳过其中的一些行。

出于同样的原因，不支持完整连接。

Anti和Semi连接

反连接和半连接的相似之处在于，对于第一个(外部)集合的每一行，在第二个(内部)集合中只找到一个匹配行就足够了。

反连接只返回第一个集合的行，如果它们在第二个集合中没有匹配：一旦执行器在第二个集合中找到第一个匹配的行，它就可以退出当前循环：第一个集合的对应行必须从结果中排除。

反连接可用于计算NOT EXISTS谓词。

例如，让我们寻找机舱配置未定义的飞机模型。对应的计划包含嵌套循环反连接节点：

没有NOT EXISTS谓词的另一个查询将具有相同的计划：

半连接返回第一个集合中在第二个集合中至少有一个匹配的行(同样，不需要检查集合中是否有其他匹配—结果已经知道了)。

半连接可用于计算EXISTS谓词。让我们找出机舱内安装了座椅的飞机模型：

嵌套循环半连接节点表示同名连接方法。这个计划(就像上面的反连接计划一样)提供了座椅表中行数的基本估计(rows=149)，尽管只检索其中的一行就足够了。当然，实际的查询执行在获取第一行后停止：

基数预估

半连接的选择性以通常的方式估计，只是内部集合的基数被视为1。对于反连接，估计的选择性从1中减去，就像否定一样。

成本预估

对于反连接和半连接，成本估计反映了这样一个事实:一旦找到第一个匹配行，第二组的扫描就会停止。

不等连接

嵌套循环算法允许基于任何连接条件连接行集。

显然，如果内部集是一个在其上创建了索引的基表，并且连接条件使用属于该索引的操作符类的操作符，则对内部集的访问可能非常有效。但是，总是可以通过计算经过某些条件过滤的行的笛卡尔积来执行连接——在本例中，这些条件完全可以是任意的。就像下面的查询一样，它选择彼此靠近的机场对：

并行模式

嵌套循环连接可以参与并行计划执行。

只有外层的一组可以并行处理，因为它可以被几个工人同时扫描。获取外部行后，每个worker必须在内部集中搜索匹配的行，这是顺序完成的。

下面显示的查询包括几个连接；它搜索拥有特定航班机票的乘客：

在上层，按顺序执行嵌套循环连接。外部集合由唯一键获取的航班表的一行组成，因此即使对于大量的内部行，也可以使用嵌套循环。

使用并行计划检索内部集合。每个工作线程扫描ticket_flights表中属于自己的那部分行，并使用嵌套循环算法将它们与机票连接起来。