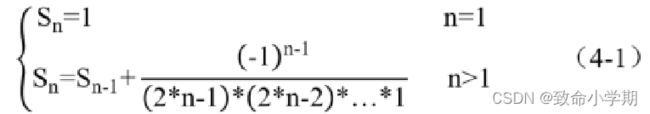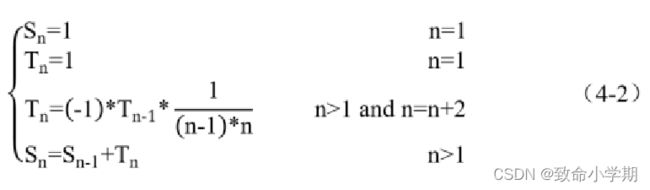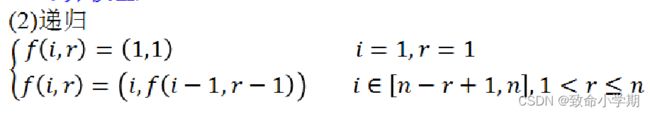【算法设计zxd】第一章 算法基础 4.设计工具【三角矩阵,】
目录
1. 循环设计
(1) 设计思维
自底向上的设计(Down - Top Design)
自顶向下的设计(Top-Down Design)
(2)挖掘内在规律构建计算模型
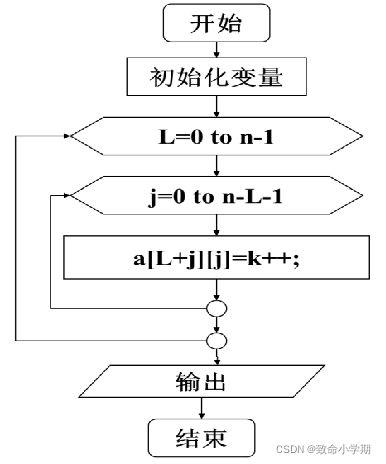
【例1-3】设计算法,输出一个n×n的三角矩阵,如图所示规律。
问题分析:
计算模型:
算法设计与描述:
算法分析:
算法实现:
(3)改进计算模型提高运算效率
【例1-4】
问题分析
计算模型
算法设计与描述
算法实现:
2. 递归设计
递归设计的步骤:
【1-5】运用递归方式设计求解斐波那契数列(Fibonacci sequence)的第n项的值
计算模型
算法分析
3.循环与递归的比较
【例1-5】任意给定十进制数:(1)从低位到高位逐位输出各位数字; (2) 从高位到低位逐位输出各位数字。
问题分析
算法实现
【例1-6】求从n个自然数(1,2,3,…, n)中取出r个数的所有组合。
计算模型:1)循环算法:
2)递归
算法实现
【1-7】找出n个自然数(1,2,3,…, n)中取出r个数的所有组合。
算法分析
算法设计与描述
比较总结:
1. 循环设计
(1) 设计思维
自底向上的设计(Down - Top Design)
先找出某个问题的子问题或若干特殊问题,
以定性、定量的方式去描述和解决这些子问题,
然后,逐步合并子问题的解,最后得到大问题的解。
核心本质:合并
自顶向下的设计(Top-Down Design)
将复杂的大问题分解为相对简单的小问题,
找出每个问题的关键、重点所在,
然后用精确的思维定性、定量地去描述问题和解决问题。
核心本质:分解。
例如:归并算法:自顶向下拆,自底向上合并
(2)挖掘内在规律构建计算模型
挖掘问题的内在规律,进行抽象并构建计算模型
交通指挥灯:数据构造
三角矩阵:运算规律
运算规律:一般找下标对应规律 最快
【例1-3】设计算法,输出一个n×n的三角矩阵,如图所示规律。
行列参与运算(下标)
问题分析:
问题:要找到按斜行访问与按矩阵访问之间的映射关系?
计算模型:
算法设计与描述:
输入:矩阵行列值n
输出:按斜行元素值为连续整数的三角矩阵
算法分析:
其中,L代表斜行,j代表列。
【其实是每一个元素都进行操作,且只进行一次。所以执行次数=元素个数】
【第一斜行n 第二斜行......】
算法实现:
#include
int main()
{
// 输入
int n,k=1;
int a[100][100];
printf("请输入n值:");
scanf("%d",&n);
for(int L=0;L 思考题:n=5*5?
代码:
#include
using namespace std;
int main()
{
int n=5*5;
int k=0;
int a[n][n];
for (int i=0;i 结果:
0 0 1
0 1 2
0 2 3
0 3 4
1 0 5
1 1 6
1 2 7
2 0 8
2 1 9
3 0 10
1
5 2
8 6 3
10 9 7 4(3)改进计算模型提高运算效率
【例1-4】求1/1!-1/3!+1/5!-1/7!+…+(-1)n+1/(2*n-1)!
① 问题分析 (运算过滤)
迭代方法是在累乘的基础上实现累加
②计算模型
③算法设计与描述
| 依据式(4-1)设计的算法EA |
依据式(4-2)设计的算法EA_G |
||
| 输入 |
计算范围n |
||
| 输出 |
累加结果S |
||
| 算法 描述 |
step 1: 读入n,令S=T=1、i=3、j=1,n=2*n-1 step 2: 判断i<=n,成立T=1转step3, 否则进入step 6 step 3: 判断j<=i,成立转step 4, 否则进入step5 step 4: 执行T=T*j, j=j+1; 转step 3; step 5: 计算T的符号; step 6: S=S+1/T; i=i+2; 转step 2; step 7: 输出S,运算结束。 |
step 1: 读入n,令S=T=1、i=3,n=2*n-1 step 2: 判断i<=n,成立转step3, 否则进入step 5 step 3: T=(-1)*T*(i-1)*i; step 4: S=S+1/T; i=i+2; 转step 2; step 5: 输出S,运算结束。 |
|
| 3 4是内层循环 | 少去内层循环 | ||
④算法分析(缺)
⑤算法实现:
EA
// EA
#include
int main()
{
float s=1.0f,t;
int n,count=2;//项数
printf("请输入计算项数:");
scanf("%d",&n);
for(int i=3;i<=2*n-1;i+=2)
{
t=1.0f;//每次都重新算
for(int j=2;j<=i;j++)//分母
{
t=t*j;
}
for(int j=1;j<=count+1;j++)
{
t=-t;
}
s=s+ 1/t;
count++;
}
printf("s=%f\n",s);
} EA_G
// EA _ G
#include
int main()
{
float s=1.0f,t=1.0f;
int n;
printf("请输入计算项数:");
scanf("%d",&n);
for(int i=3;i<=2*n-1;i+=2)
{
t= -t*(i-1)*i;//计算分母
s=s+ 1/t;
}
printf("s=%f\n",s);
} ⑥测试
⑦结果整理与文件编制
2. 递归设计
定义:一个过程或函数在定义中直接或间接调用自身的一种方法。
设计关键:找出递归关系(方程)和递归终止(边界)条件。递归关系就是使问题向边界条件转化的规则。
递归设计的步骤:
(1) 分析问题找到递归关系:找出大规模问题与小规模问题的关系,以便通过递归使问题规模变小。(收敛的)
(2)设置终止条件控制递归:通过停止条件的设置,找出可解的最小规模问题。
(3)设计函数确定数据传递方式。
【1-5】斐波那契的第n项 递归
运用递归方式设计求解斐波那契数列(Fibonacci sequence)的第n项的值
计算模型
递归的终止条件和递归方程,如下:
其中,式(5-2)是递归方程,式(5-1)是终止条件。
算法分析
依据计算模型,容易得知,求第n项的值需要计算n-2次,所以,主体算法计算次数约为f(n)=n-2
斐波那契:算法实现 C
#include
int fcc(int n)
{
int t;
if(n==1|n==2)return 1;
else return fcc(n-1)+fcc(n-2);
}
int main()
{
int n;
printf("input n:");
scanf("%d",&n);
printf("No.%d value of Fibonacci sequence is %d\n ",n,fcc(n));
return 0;
} 3.循环与递归的比较
每个迭代算法原则上总可以转换成与它等价的递归算法;
反之则不然,
就是说不是每个递归算法都可以转换成与它等价的循环结构算法。
【例1-5】任意给定十进制数:(1)从低位到高位逐位输出各位数字; (2) 从高位到低位逐位输出各位数字。
问题分析
这是一个较为简单的问题,我们将从实现的角度来比较两者对于问题的适应性。
算法实现
(1)从低位到高位:效率实际一样
(2)从高位到低位:循环首先需要确定位数,递归——联系到树的先根遍历和中 后
改变要求,递归变化可能极小
思考题:尝试总结 递归与循环 的优缺点
思考题:用递归求出斐波那契数列 去除重复计算
#include
using namespace std;
//递归
int fb(int i)
{
if(i==1||i==2)return 1;
else return fb(i-1)+fb(i-2);
}
//时间复杂度O(2^n)
//空间复杂度O(1)
//数组,去重,用空间换时间
int a[40];
int fib(int n)
{
a[0]=0;
a[1]=1;
for(int i=2;i<=n;i++)
{
a[i]=a[i-1]+a[i-2];
}
return a[n];
}
//时间O(n)
//空间O(n)
//动态规划
int fibdp(int n)
{
int f=0;
int fp=1;
while(n--)
{
fp=fp+f;//规则
f=fp-f;//恢复fplus
}
return f;
}
//时间O(n)
//空间O(1)
int main()
{
cout< 代码:
#include
using namespace std;
void gaocir(int n)
{
int b[20];
int i=0;
while(n)
{
b[i]=n%10;
n=n/10;
i++;
}
while(i--)
{
cout<<" "< 【例1-6】求从n个自然数(1,2,3,…, n)中取出r个数的所有组合。
计算模型:
1)循环算法:
其中, 1 ≤ r ≤ n , 且 r 在循环算法实现时 代表循环嵌套的层数,必须是定值。
2)递归
算法实现
算法分析
算法设计与描述
比较总结:
| 递归 |
循环 |
|
| 程序可读性 |
易 |
难 |
| 代码量大小 |
小 |
大 |
| 时间 |
长 |
短 |
| 占用空间 |
大 |
小 |
| 适用范围 |
广 |
窄 |
| 设计难度 |
易 |
难 |