【路径规划】OSQP曲线平滑 公式及代码
参考与前言
-
apollo 代码:https://github.com/ApolloAuto/apollo/tree/master/modules/planning/math/smoothing_spline
-
apollo readme:https://github.com/ApolloAuto/apollo/blob/master/docs/specs/qp_spline_path_optimizer.md
-
自我测试的代码:张聪明/OSQP_test (gitee.com)
本篇也主要基于参考二翻译而来,背景是因为 GPIR代码 里有这层做初始化,不太懂怎么干的和干啥,所以就搜索了一下,一开始一直在弄参考三使其能逐步断点debug 以让我能明了整个步骤,不过后来搜了一下看到了参考二 emm 就是我想要了解的 smooth到底是怎样编程二次规划问题的。
以下大部分翻译至参考二,其中添加了自己的思考句子(有时也可能就是问题
实际这个包的名字就:QP-Spline-Path Optimizer,基于二次规划的曲线路径优化器
方法:Quadratic programming + Spline interpolation,二次规划 + 样条差值
注意这全文都是讲的path,而不是trajectory,至于两者区别:Motion Planning 是什么 总结了下:
Path是静态的,不包括时间;Trajectory是除了路径还有其他信息可以说是时间,speed profile,这条路径上速度的变化关系
这一段是我看完了写的:emmm 看完了发现包装的太好了 以至于就算看了整个公式 对应起来都是要跳转进去的 果然是做软件一套的。但是想着用的话 这样也算是够了的。所以整体其实还是拿五次样条先生成了reference point 然后根据他们的s,l点来进行约束,cost function也已经给出
优美格式及后续错误更新见:https://www.cnblogs.com/kin-zhang/p/15532655.html
谁让… 这边广告 弹出等太多了… 哎
① 目标函数 Objective function
路径长度
首先路径的坐标系是以SL 也就是frenet坐标系下。其中 s 是从车辆当前位置到规划路径的长度,类似于我们会提前给定一个 我们要规划多长的距离。
样条线段
将路径拆分成 n 段。每段都用多项式表示,比如这样一个式子:
每段 i 沿着参考线的累积距离 d i d_i di 的多项式函数公式如下:
l = f i ( s ) = a i 0 + a i 1 ⋅ s + a i 2 ⋅ s 2 + a i 3 ⋅ s 3 + a i 4 ⋅ s 4 + a i 5 ⋅ s 5 ( 0 ≤ s ≤ d i ) (1) l = f_i(s) = a_{i0} + a_{i1} \cdot s + a_{i2} \cdot s^2 + a_{i3} \cdot s^3 + a_{i4} \cdot s^4 + a_{i5} \cdot s^5 (0 \leq s \leq d_{i}) \tag{1} l=fi(s)=ai0+ai1⋅s+ai2⋅s2+ai3⋅s3+ai4⋅s4+ai5⋅s5(0≤s≤di)(1)
实际代码调用时,后者的 5 也就是五次多项式的意思
OsqpSpline2dSolver osqp_spline2d_solver(t_knots, 5);
线段的优化函数
也就是一个cost 和为速度,加速度,加加速度:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ cost = \sum_{i…
但实际test.cc这个代码中只对加加速度进行了weight赋值,所以最后在计算曲率 curvature的时候 smooth后的效果明显好很多(虽然点之间看不出来啥)
mutable_kernel->Add2dThirdOrderDerivativeMatrix(0.5);
将cost函数转为QP形式
QP formulation:
m i n i m i z e 1 2 ⋅ x T ⋅ H ⋅ x + f T ⋅ x s . t . L B ≤ x ≤ U B A e q x = b e q A x ≥ b \begin{aligned} minimize & \frac{1}{2} \cdot x^T \cdot H \cdot x + f^T \cdot x \\ s.t. \qquad & LB \leq x \leq UB \\ & A_{eq}x = b_{eq} \\ & Ax \geq b \end{aligned} minimizes.t.21⋅xT⋅H⋅x+fT⋅xLB≤x≤UBAeqx=beqAx≥b
下面是如何被优化函数objective function/cost function转成QP形式,首先我们 (1)式 可以转成向量相乘的形式,那么 f i ( s ) f_i(s) fi(s) 可以这样表示
f i ( s ) = ∣ 1 s s 2 s 3 s 4 s 5 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ f_i(s) = \begin{vmatrix} 1 & s & s^2 & s^3 & s^4 & s^5 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} fi(s)=∣∣1ss2s3s4s5∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣
f i ′ ( s ) f_i'(s) fi′(s) 求导再次表示
f i ′ ( s ) = ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ f_i'(s) = \begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} fi′(s)=∣∣012s3s24s35s4∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣
f i ′ ( s ) 2 f_i'(s)^2 fi′(s)2 两个相乘一下:
f i ′ ( s ) 2 = ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ⋅ ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ ⋅ ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ f_i'(s)^2 = \begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix} \cdot \begin{vmatrix} 0 \\ 1 \\ 2s \\ 3s^2 \\ 4s^3 \\ 5s^4 \end{vmatrix} \cdot \begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} fi′(s)2=∣∣ai0ai1ai2ai3ai4ai5∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣012s3s24s35s4∣∣∣∣∣∣∣∣∣∣∣∣⋅∣∣012s3s24s35s4∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣
然后就会获得这样的:
∫ 0 d i f i ′ ( s ) 2 d s = ∫ 0 d i ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ⋅ ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ ⋅ ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ d s \int\limits_{0}^{d_i} f_i'(s)^2 ds = \int\limits_{0}^{d_i} \begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix} \cdot \begin{vmatrix} 0 \\ 1 \\ 2s \\ 3s^2 \\ 4s^3 \\ 5s^4 \end{vmatrix} \cdot \begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} ds 0∫difi′(s)2ds=0∫di∣∣ai0ai1ai2ai3ai4ai5∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣012s3s24s35s4∣∣∣∣∣∣∣∣∣∣∣∣⋅∣∣012s3s24s35s4∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣ds
把常数项提到积分外面去:
∫ 0 d i f ′ ( s ) 2 d s = ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ⋅ ∫ 0 d i ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ ⋅ ∣ 0 1 2 s 3 s 2 4 s 3 5 s 4 ∣ d s ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ \int\limits_{0}^{d_i} f'(s)^2 ds = \begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix} \cdot \int\limits_{0}^{d_i} \begin{vmatrix} 0 \\ 1 \\ 2s \\ 3s^2 \\ 4s^3 \\ 5s^4 \end{vmatrix} \cdot \begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix} ds \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} 0∫dif′(s)2ds=∣∣ai0ai1ai2ai3ai4ai5∣∣⋅0∫di∣∣∣∣∣∣∣∣∣∣∣∣012s3s24s35s4∣∣∣∣∣∣∣∣∣∣∣∣⋅∣∣012s3s24s35s4∣∣ds⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣
= ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ⋅ ∫ 0 d i ∣ 0 0 0 0 0 0 0 1 2 s 3 s 2 4 s 3 5 s 4 0 2 s 4 s 2 6 s 3 8 s 4 10 s 5 0 3 s 2 6 s 3 9 s 4 12 s 5 15 s 6 0 4 s 3 8 s 4 12 s 5 16 s 6 20 s 7 0 5 s 4 10 s 5 15 s 6 20 s 7 25 s 8 ∣ d s ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ =\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix} \cdot \int\limits_{0}^{d_i} \begin{vmatrix} 0 & 0 &0&0&0&0\\ 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4\\ 0 & 2s & 4s^2 & 6s^3 & 8s^4 & 10s^5\\ 0 & 3s^2 & 6s^3 & 9s^4 & 12s^5&15s^6 \\ 0 & 4s^3 & 8s^4 &12s^5 &16s^6&20s^7 \\ 0 & 5s^4 & 10s^5 & 15s^6 & 20s^7 & 25s^8 \end{vmatrix} ds \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} =∣∣ai0ai1ai2ai3ai4ai5∣∣⋅0∫di∣∣∣∣∣∣∣∣∣∣∣∣000000012s3s24s35s402s4s26s38s410s503s26s39s412s515s604s38s412s516s620s705s410s515s620s725s8∣∣∣∣∣∣∣∣∣∣∣∣ds⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣
然后给矩阵里的都积分一下从0到 d i d_i di 积分一下 就可以获得这样的:
∫ 0 d i f i ′ ( s ) 2 d s = ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ⋅ ∣ 0 0 0 0 0 0 0 d i d i 2 d i 3 d i 4 d i 5 0 d i 2 4 3 d i 3 6 4 d i 4 8 5 d i 5 10 6 d i 6 0 d i 3 6 4 d i 4 9 5 d i 5 12 6 d i 6 15 7 d i 7 0 d i 4 8 5 d i 5 12 6 d i 6 16 7 d i 7 20 8 d i 8 0 d i 5 10 6 d i 6 15 7 d i 7 20 8 d i 8 25 9 d i 9 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ \int\limits_{0}^{d_i} f'_i(s)^2 ds =\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix} \cdot \begin{vmatrix} 0 & 0 & 0 & 0 &0&0\\ 0 & d_i & d_i^2 & d_i^3 & d_i^4&d_i^5\\ 0& d_i^2 & \frac{4}{3}d_i^3& \frac{6}{4}d_i^4 & \frac{8}{5}d_i^5&\frac{10}{6}d_i^6\\ 0& d_i^3 & \frac{6}{4}d_i^4 & \frac{9}{5}d_i^5 & \frac{12}{6}d_i^6&\frac{15}{7}d_i^7\\ 0& d_i^4 & \frac{8}{5}d_i^5 & \frac{12}{6}d_i^6 & \frac{16}{7}d_i^7&\frac{20}{8}d_i^8\\ 0& d_i^5 & \frac{10}{6}d_i^6 & \frac{15}{7}d_i^7 & \frac{20}{8}d_i^8&\frac{25}{9}d_i^9 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} 0∫difi′(s)2ds=∣∣ai0ai1ai2ai3ai4ai5∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣0000000didi2di3di4di50di234di346di458di5610di60di346di459di5612di6715di70di458di5612di6716di7820di80di5610di6715di7820di8925di9∣∣∣∣∣∣∣∣∣∣∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣
所以现在应该发现了:如果是五次样条曲线的导数cost函数是会获得一个 6 × 6 6\times6 6×6的矩阵
② 约束 Constraints
初始点/end点约束
init point/初始点
假设第一个点是 ( s 0 s_0 s0, l 0 l_0 l0), ( s 0 s_0 s0, l 0 ′ l'_0 l0′) and ( s 0 s_0 s0, l 0 ′ ′ l''_0 l0′′), 其中 l 0 l_0 l0 , l 0 ′ l'_0 l0′ and l 0 ′ ′ l''_0 l0′′ 是规划初始点的横向offset及其一阶导、二阶导,可以由 f i ( s ) f_i(s) fi(s), f i ′ ( s ) f'_i(s) fi′(s), and f i ( s ) ′ ′ f_i(s)'' fi(s)′′ 计算得知
使用这个式子,将这些约束转为QP等式约束
A e q x = b e q A_{eq}x = b_{eq} Aeqx=beq
下面就是转换的步骤:
f i ( s 0 ) = ∣ 1 s 0 s 0 2 s 0 3 s 0 4 s 0 5 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ = l 0 f_i(s_0) = \begin{vmatrix} 1 & s_0 & s_0^2 & s_0^3 & s_0^4&s_0^5 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5}\end{vmatrix} = l_0 fi(s0)=∣∣1s0s02s03s04s05∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣=l0
f i ′ ( s 0 ) = ∣ 0 1 2 s 0 3 s 0 2 4 s 0 3 5 s 0 4 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ = l 0 ′ f'_i(s_0) = \begin{vmatrix} 0& 1 & 2s_0 & 3s_0^2 & 4s_0^3 &5 s_0^4 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} = l'_0 fi′(s0)=∣∣012s03s024s035s04∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣=l0′
f i ′ ′ ( s 0 ) = ∣ 0 0 2 3 × 2 s 0 4 × 3 s 0 2 5 × 4 s 0 3 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ = l 0 ′ ′ f''_i(s_0) = \begin{vmatrix} 0&0& 2 & 3\times2s_0 & 4\times3s_0^2 & 5\times4s_0^3 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} = l''_0 fi′′(s0)=∣∣0023×2s04×3s025×4s03∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣=l0′′
其中 i i i 是指那段拥有初始点 s 0 s_0 s0 的分段区,应该说是最初的那段,因为后面平滑约束的时候还有 f k + 1 ( s 0 ) f_{k+1}(s_0) fk+1(s0)上面三个一起形成了一个等式,即最后的形式如 式(2).
end point/结束点
与上述的initial point 初始点步骤一致,结束点 ( s e , l e ) (s_e, l_e) (se,le) 也是已知的,而且应该是和前面的约束一致的形式,所以总一总可以得出
等式约束 A e q x = b e q A_{eq}x = b_{eq} Aeqx=beq 展开为以下形式
∣ 1 s 0 s 0 2 s 0 3 s 0 4 s 0 5 0 1 2 s 0 3 s 0 2 4 s 0 3 5 s 0 4 0 0 2 3 × 2 s 0 4 × 3 s 0 2 5 × 4 s 0 3 1 s e s e 2 s e 3 s e 4 s e 5 0 1 2 s e 3 s e 2 4 s e 3 5 s e 4 0 0 2 3 × 2 s e 4 × 3 s e 2 5 × 4 s e 3 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ = ∣ l 0 l 0 ′ l 0 ′ ′ l e l e ′ l e ′ ′ ∣ (2) \begin{vmatrix} 1 & s_0 & s_0^2 & s_0^3 & s_0^4&s_0^5 \\ 0&1 & 2s_0 & 3s_0^2 & 4s_0^3 & 5s_0^4 \\ 0& 0&2 & 3\times2s_0 & 4\times3s_0^2 & 5\times4s_0^3 \\ 1 & s_e & s_e^2 & s_e^3 & s_e^4&s_e^5 \\ 0&1 & 2s_e & 3s_e^2 & 4s_e^3 & 5s_e^4 \\ 0& 0&2 & 3\times2s_e & 4\times3s_e^2 & 5\times4s_e^3 \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} = \begin{vmatrix} l_0\\ l'_0\\ l''_0\\ l_e\\ l'_e\\ l''_e\\ \end{vmatrix}\tag{2} ∣∣∣∣∣∣∣∣∣∣∣∣100100s010se10s022s02se22se2s033s023×2s0se33se23×2ses044s034×3s02se44se34×3se2s055s045×4s03se55se45×4se3∣∣∣∣∣∣∣∣∣∣∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣=∣∣∣∣∣∣∣∣∣∣∣∣l0l0′l0′′lele′le′′∣∣∣∣∣∣∣∣∣∣∣∣(2)
实际代码中为:
// init point constraint
mutable_constraint->Add2dPointConstraint(0, Eigen::Vector2d(spline(a, 0), spline(b, 0)));
mutable_constraint->Add2dPointDerivativeConstraint(0, Eigen::Vector2d(spline_1st(a, 0), spline_1st(b, 0)));
// end point constraint
mutable_constraint->Add2dPointConstraint(t_end, Eigen::Vector2d(spline(a, t_end), spline(b, t_end)));
mutable_constraint->Add2dPointDerivativeConstraint(t_end, Eigen::Vector2d(spline_1st(a, t_end), spline_1st(b, t_end)));
分段之间平滑约束
这部分的约束主要在于将分段点连接处进行平滑操作,比如一阶连续,二阶连续,三阶连续。
假设 s e g k seg_k segk 和 s e g k + 1 seg_{k+1} segk+1 是相连接的, s e g k seg_k segk 段累积的 s 距离值为 s k s_k sk. 注意这里的 s 0 s_0 s0 不同与前面说的为整段路径的init point初始点,而是每段自身的起点处,所以对 s e g k seg_k segk 来说他的累积距离 s k s_k sk 正是 s e g k + 1 seg_{k+1} segk+1 的起点 s 0 s_0 s0
f k ( s k ) = f k + 1 ( s 0 ) f_k(s_k) = f_{k+1} (s_0) fk(sk)=fk+1(s0)
以下为计算过程:
∣ 1 s k s k 2 s k 3 s k 4 s k 5 ∣ ⋅ ∣ a k 0 a k 1 a k 2 a k 3 a k 4 a k 5 ∣ = ∣ 1 s 0 s 0 2 s 0 3 s 0 4 s 0 5 ∣ ⋅ ∣ a k + 1 , 0 a k + 1 , 1 a k + 1 , 2 a k + 1 , 3 a k + 1 , 4 a k + 1 , 5 ∣ \begin{vmatrix} 1 & s_k & s_k^2 & s_k^3 & s_k^4&s_k^5 \\ \end{vmatrix} \cdot \begin{vmatrix} a_{k0} \\ a_{k1} \\ a_{k2} \\ a_{k3} \\ a_{k4} \\ a_{k5} \end{vmatrix} = \begin{vmatrix} 1 & s_{0} & s_{0}^2 & s_{0}^3 & s_{0}^4&s_{0}^5 \\ \end{vmatrix} \cdot \begin{vmatrix} a_{k+1,0} \\ a_{k+1,1} \\ a_{k+1,2} \\ a_{k+1,3} \\ a_{k+1,4} \\ a_{k+1,5} \end{vmatrix} ∣∣1sksk2sk3sk4sk5∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ak0ak1ak2ak3ak4ak5∣∣∣∣∣∣∣∣∣∣∣∣=∣∣1s0s02s03s04s05∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ak+1,0ak+1,1ak+1,2ak+1,3ak+1,4ak+1,5∣∣∣∣∣∣∣∣∣∣∣∣
∣ 1 s k s k 2 s k 3 s k 4 s k 5 − 1 − s 0 − s 0 2 − s 0 3 − s 0 4 − s 0 5 ∣ ⋅ ∣ a k 0 a k 1 a k 2 a k 3 a k 4 a k 5 a k + 1 , 0 a k + 1 , 1 a k + 1 , 2 a k + 1 , 3 a k + 1 , 4 a k + 1 , 5 ∣ = 0 \begin{vmatrix} 1 & s_k & s_k^2 & s_k^3 & s_k^4&s_k^5 & -1 & -s_{0} & -s_{0}^2 & -s_{0}^3 & -s_{0}^4&-s_{0}^5\\ \end{vmatrix} \cdot \begin{vmatrix} a_{k0} \\ a_{k1} \\ a_{k2} \\ a_{k3} \\ a_{k4} \\ a_{k5} \\ a_{k+1,0} \\ a_{k+1,1} \\ a_{k+1,2} \\ a_{k+1,3} \\ a_{k+1,4} \\ a_{k+1,5} \end{vmatrix} = 0 ∣∣1sksk2sk3sk4sk5−1−s0−s02−s03−s04−s05∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣ak0ak1ak2ak3ak4ak5ak+1,0ak+1,1ak+1,2ak+1,3ak+1,4ak+1,5∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣=0
使用 s 0 s_0 s0 = 0 在上式中,然后同样添加如下的等式约束:
f k ′ ( s k ) = f k + 1 ′ ( s 0 ) f k ′ ′ ( s k ) = f k + 1 ′ ′ ( s 0 ) f k ′ ′ ′ ( s k ) = f k + 1 ′ ′ ′ ( s 0 ) f'_k(s_k) = f'_{k+1} (s_0) \\ f''_k(s_k) = f''_{k+1} (s_0) \\ f'''_k(s_k) = f'''_{k+1} (s_0) fk′(sk)=fk+1′(s0)fk′′(sk)=fk+1′′(s0)fk′′′(sk)=fk+1′′′(s0)
实际代码中只添加了三阶连续:(但是三阶连续的前提不是一二阶也连续吗?)
mutable_constraint->Add2dThirdDerivativeSmoothConstraint();
对采样点的边界约束
沿着路径均匀采样 m 个点,检查这些点是否触碰到了障碍物的边界,然后将其转成QP问题的不等式约束:
A x ≥ b Ax \geq b Ax≥b
首先根据道路宽度和周围障碍物找到点 ( s j , l j ) (s_j, l_j) (sj,lj) and j ∈ [ 0 , m ] j\in[0, m] j∈[0,m] 的下边界 l l b , j l_{lb,j} llb,j,然后不等式约束的计算如下:
∣ 1 s 0 s 0 2 s 0 3 s 0 4 s 0 5 1 s 1 s 1 2 s 1 3 s 1 4 s 1 5 . . . . . . . . . . . . . . . . . . 1 s m s m 2 s m 3 s m 4 s m 5 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ≥ ∣ l l b , 0 l l b , 1 . . . l l b , m ∣ (10) \begin{vmatrix} 1 & s_0 & s_0^2 & s_0^3 & s_0^4&s_0^5 \\ 1 & s_1 & s_1^2 & s_1^3 & s_1^4&s_1^5 \\ ...&...&...&...&...&... \\ 1 & s_m & s_m^2 & s_m^3 & s_m^4&s_m^5 \\ \end{vmatrix} \cdot \begin{vmatrix}a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} \geq \begin{vmatrix} l_{lb,0}\\ l_{lb,1}\\ ...\\ l_{lb,m}\\ \end{vmatrix} \tag{10} ∣∣∣∣∣∣∣∣11...1s0s1...sms02s12...sm2s03s13...sm3s04s14...sm4s05s15...sm5∣∣∣∣∣∣∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣≥∣∣∣∣∣∣∣∣llb,0llb,1...llb,m∣∣∣∣∣∣∣∣(10)
-
为什么会有下界?根据采样的想法应该只有上界才对,或者说下界可以为完全不进行横向采样扩张
杰哥回复:这是一个box形状,不是说从0-10是我的采样增加区间 而是以ref为0,-10 - 10采样增加区间
-
为什么实际代码中是横纵向都有限制?采样点扩张如上问中
lower_bound.emplace_back(d_lateral - lat_tol[i]); lower_bound.emplace_back(d_longitudinal - lon_tol[i]); upper_bound.emplace_back(d_lateral + lat_tol[i]); upper_bound.emplace_back(d_longitudinal + lon_tol[i]);如此手绘图所示:
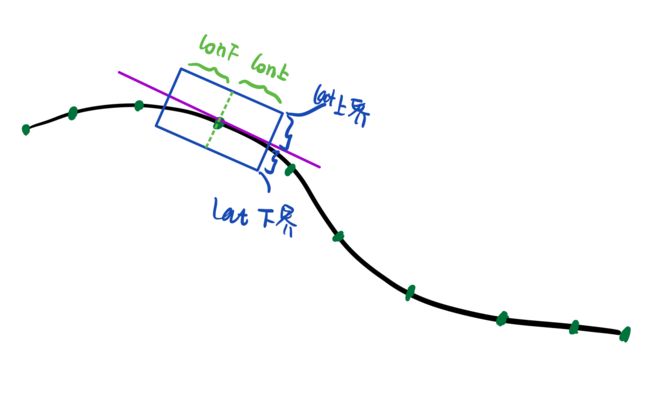
-
这里没有办法根据障碍物加进去边界条件?
好像可以对某一个 l u b , j l_{ub,j} lub,j 进行扩大,使其表达障碍物的膨胀。但是我感觉这个点应该是说已知环境中,不包括动态障碍物,类似于在地图已经建好的这层上去做边界约束,而不是实时根据障碍物去做约束
这样的 因为输入的边界约束是station lateral boundary,其实是依据你的reference line 参考线然后有设定纵向和横向的最大便宜角度进去,比如test代码中是0.2
同样的,上界 l u b , j l_{ub,j} lub,j 同样也可以以这种不等式约束计算:
∣ − 1 − s 0 − s 0 2 − s 0 3 − s 0 4 − s 0 5 − 1 − s 1 − s 1 2 − s 1 3 − s 1 4 − s 1 5 . . . . . . − . . . . . . . . . . . . − 1 − s m − s m 2 − s m 3 − s m 4 − s m 5 ∣ ⋅ ∣ a i 0 a i 1 a i 2 a i 3 a i 4 a i 5 ∣ ≥ − 1 ⋅ ∣ l u b , 0 l u b , 1 . . . l u b , m ∣ (11) \begin{vmatrix} -1 & -s_0 & -s_0^2 & -s_0^3 & -s_0^4&-s_0^5 \\ -1 & -s_1 & -s_1^2 & -s_1^3 & -s_1^4&-s_1^5 \\ ...&...-&...&...&...&... \\ -1 & -s_m & -s_m^2 & -s_m^3 & -s_m^4&-s_m^5 \\ \end{vmatrix} \cdot \begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} \geq -1 \cdot \begin{vmatrix} l_{ub,0}\\ l_{ub,1}\\ ...\\ l_{ub,m}\\ \end{vmatrix} \tag{11} ∣∣∣∣∣∣∣∣−1−1...−1−s0−s1...−−sm−s02−s12...−sm2−s03−s13...−sm3−s04−s14...−sm4−s05−s15...−sm5∣∣∣∣∣∣∣∣⋅∣∣∣∣∣∣∣∣∣∣∣∣ai0ai1ai2ai3ai4ai5∣∣∣∣∣∣∣∣∣∣∣∣≥−1⋅∣∣∣∣∣∣∣∣lub,0lub,1...lub,m∣∣∣∣∣∣∣∣(11)
③ 代码总结
首先完整的test代码可见gitee链接,此处仅将上述提到的进行说明
// solver
OsqpSpline2dSolver osqp_spline2d_solver(t_knots, 5);
mutable_kernel->Add2dReferenceLineKernelMatrix(t_coord, ref_ft, 0.5);
// 添加连续平滑约束 三阶
mutable_constraint->Add2dThirdDerivativeSmoothConstraint();
// 添加初始点
mutable_constraint->Add2dPointConstraint(0, Eigen::Vector2d(spline(a, 0), spline(b, 0)));
mutable_constraint->Add2dPointDerivativeConstraint(0, Eigen::Vector2d(spline_1st(a, 0), spline_1st(b, 0)));
// 添加end point
double t_end = t_coord.back();
mutable_constraint->Add2dPointConstraint(t_end, Eigen::Vector2d(spline(a, t_end), spline(b, t_end)));
mutable_constraint->Add2dPointDerivativeConstraint(t_end, Eigen::Vector2d(spline_1st(a, t_end), spline_1st(b, t_end)));
// 添加边界约束
mutable_constraint->Add2dStationLateralBoundary(t_coord, ref_ft, ref_theta,lon_tol, lat_tol);
实际上看上去 数学公式都被隐去了 是因为osqp这层 apollo加了自己的spline,所以最后main呈现的就是这样的形式,如果跳转各个部分的更为仔细的可以发现更多,比如添加边界约束:
bool Spline2dConstraint::Add2dStationLateralBoundary(
const std::vector<double>& t, const vector_Eigen<Eigen::Vector2d>& ref_xy,
const std::vector<double>& ref_theta, const std::vector<double>& lon_tol,
const std::vector<double>& lat_tol) {
if (t.size() != ref_xy.size() || ref_xy.size() != ref_theta.size() ||
ref_theta.size() != lon_tol.size() || lon_tol.size() != lat_tol.size()) {
return false;
}
Eigen::MatrixXd sl_constraints =
Eigen::MatrixXd::Zero(2 * t.size(), total_param_);
std::vector<double> lower_bound, upper_bound;
for (uint32_t i = 0; i < t.size(); ++i) {
const uint32_t index = FindSegStartIndex(t[i]);
const double d_lateral = SignDistance(ref_xy[i], ref_theta[i]);
const double d_longitudinal =
SignDistance(ref_xy[i], ref_theta[i] - M_PI_2);
const double t_corrected = t[i] - t_knots_[index];
std::vector<double> lateral_coef = AffineCoef(ref_theta[i], t_corrected);
std::vector<double> longitudianl_coef =
AffineCoef(ref_theta[i] - M_PI_2, t_corrected);
const uint32_t index_offset = index * spline_param_num_;
// 构建公式10,11的左边矩阵
for (uint32_t j = 0; j < spline_param_num_; ++j) {
sl_constraints(2 * i, index_offset + j) = lateral_coef[j];
sl_constraints(2 * i, index_offset + total_param_ / 2 + j) =
lateral_coef[spline_param_num_ + j];
sl_constraints(2 * i + 1, index_offset + j) = longitudianl_coef[j];
sl_constraints(2 * i + 1, index_offset + total_param_ / 2 + j) =
longitudianl_coef[spline_param_num_ + j];
}
lower_bound.emplace_back(d_lateral - lat_tol[i]);
lower_bound.emplace_back(d_longitudinal - lon_tol[i]);
upper_bound.emplace_back(d_lateral + lat_tol[i]);
upper_bound.emplace_back(d_longitudinal + lon_tol[i]);
}
return coxy_constraint_.AddConstraint(sl_constraints, lower_bound,
upper_bound);
}
由这里我们可以看到公式 10 和公式 11的矩阵形式的构建
④ 效果示意
运行上面给的Gitee代码,可以得到下面这样一幅图:

ref就是每小段都是五次样条出来的,做图就是sl坐标系下生成出来的,右图为计算了他们的每个点连接处的曲率,可以看到经过osqp spline曲率约束 cost 都有明显的生效(虽然在这个例子中展现的不大)