12 操作系统第三章 内存管理 非连续分配管理方式 基本分页存储管理 基本分段存储管理 段页式存储管理

1 基本分页存储管理

连续分配：为用户进程分配的必须是一个连续的内存空间。
非连续分配：为用户进程分配的可以是一些分散的内存空间。

1.1 什么是分页存储

1. 将内存空间分为一个个大小相等的分区（比如：每个分区4KB），每个分区就是一个“页框”（页框=页帧=内存块=物理块=物理页面）。每个页框有一个编号，即“页框号”（页框号=页帧号=内存块号=物理块号=物理页号），页框号从 0 开始 。
   

2. 将进程的逻辑地址空间也分为与页框大小相等的一个个部分， 每个部分称为一个“页”或“页面” 。每个页面也有一个编号， 即“页号”，页号也是从 0 开始 。
   

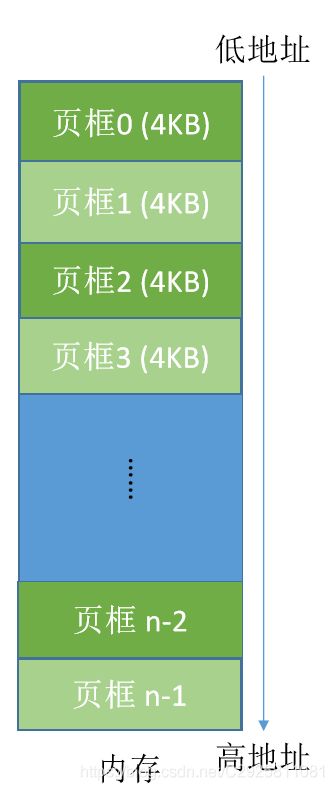
3. 操作系统以页框为单位为各个进程分配内存空间。进程的每个页面分别放入一个页框中。也就是说，进程的页面与内存的页框有一一对应的关系。 各个页面不必连续存放，可以放到不相邻的各个页框中。
   （注意：进程的最后一个页面可能没有一个页框那么大。也就是说，分页存储有可能产生内部碎片，因此页框不能太大，否则可能产生过大的内部碎片造成浪费）

1.2 重要的数据结构——页表

为了能知道进程的每个页面在内存中存放的位置，操作系统要为每个进程建立一张页表。

注：页表通常存在PCB（进程控制块）中

1. 一个进程对应一张页表
2. 进程的每个页面对应一个页表项
3. 每个页表项由“页号”和“块号”组成
4. 页表记录进程页面和实际存放的内存块之间的映射关系
5. 每个页表项的长度是相同的
   

核心问题：

1. 每个页表项多大？占几个字节？
2. 如何通过页表实现逻辑地址到物理地址的转换？

1. 已知计算机中内存块的数量→页表项中块号至少占多少字节？

假设某系统物理内存大小为4GB，页面大小为4KB，则每个页表项至少应该为多少字节？

1. 内存块大小=页面大小=4KB=2¹² B
2. 4GB的内存总共会被分为 2³²/2¹² =2²⁰个内存块
3. 内存块号的范围应该是0~ 2²⁰-1
4. 内存块号至少要用20bit来表示 →至少要用3B来表示块号（3*8=24bit）

页表项连续存放，因此页号可以是隐含的，不占存储空间（类比数组）

引出问题：假设页表中的各页表项从内存地址为X的地方开始连续存放…
如何找到页号为i的页表项？
i号页表项的存放地址=X+3*I因此，页表中的页号可以是隐含的，即页号不占用存储空间

假设某系统物理内存大小为4GB，页面大小为4KB，则每个页表项至少应该为多少字节？

1. 内存块大小=页面大小=4KB=2¹² B
2. 4GB的内存总共会被分为 2³²/2¹² =2²⁰个内存块
3. 内存块号的范围应该是0~ 2²⁰-1
4. 内存块号至少要用20bit来表示 →至少要用3B来表示块号（3*8=24bit）
5. 由于页号是隐含的，因此每个页表项占3B，存储整个页表至少需要3*(n+1)B

2. 如何实现地址的转换

进程在内存中连续存放时 ， 操作系统是如何实现逻辑地址到物理地址的转换的？
过程如下：

思考：将进程地址空间分页之后 ，操作系统该如何实现逻辑地址到物理地址的转换 ？

特点：虽然进程的各个页面是离散存放的，但是页面内部是连续存放的

如果要访问逻辑地址A，则 ：

1. 确定逻辑地址A对应的“页号”P
2. 找到P号页面在内存中的起始地址（需要查页表）
3. 确定逻辑地址A的“页内偏移量”W
   逻辑地址A对应的物理地址=P号页面在内存中的起始地址+页内偏移量W

子问题：如何确定一个逻辑地址对应的页号、页内偏移量？

Eg：在某计算机系统中，页面大小是50B。某进程逻辑地址空间大小为200B，则逻辑地址110对应的页号、页内偏移量是多少？

如何计算：
页号=逻辑地址/页面长度 （取除法的整数部分）
页内偏移量=逻辑地址%页面长度（取除法的余数部分）

本例中页号=110/50=2
页内偏移量=110%50=10

逻辑地址可以拆分为（页号，页内偏移量）
通过页号查询页表，可知页面在内存中的起始地址
页面在内存中的起始地址+页内偏移量=实际的物理地址

逻辑地址→物理地址，二进制转化

在计算机内部，地址是用二进制表示的， 如果页面大小刚好是2的整数幂，则计算机硬件可以很快速的把逻辑地址拆分成（页号，页内偏移量）

假设某计算机用32个二进制位表示逻辑地址，页面大小为4KB =2¹² B=4096B

1. 0号页的逻辑地址范围应该是0-4595，用二进制表示应该是： 00000000000000000000000000000000~00000000000000000000111111111111
2. 1号页的逻辑地址范围应该是4096~8191，用二进制表示应该是： 00000000000000000001000000000000~00000000000000000001111111111111
3. 2号页的逻辑地址范围应该是8192~12287，用二进制表示应该是： 00000000000000000010000000000000~00000000000000000010111111111111

1. Eg：逻辑地址2，用二进制表示应该是00000000000000000000000000000010
   页号=2/4096=0=00000000000000000000
   页内偏移量=2%4096=2=000000000010
2. Eg：逻辑地址4097，用二进制表示应该是00000000000000000001000000000001
   页号=4097/4096=1=00000000000000000001
   页内偏移量=4097%4096=1=000000000001

如果每个页面大小为2^KB，用二进制数表示逻辑地址， 则末尾K位即为页内偏移量，其余部分就是页号

假设物理地址也用32个二进制位表示，则由于内存块的大小=页面大小，因此：

1. 0号内存块的起始物理地址是00000000000000000000000000000000
2. 1号内存块的起始物理地址是00000000000000000001000000000000
3. 2号内存块的起始物理地址是00000000000000000010000000000000
4. 3号内存块的起始物理地址是00000000000000000011000000000000

根据页号可以查询页表，而页表中记录的只是内存块号，而不是内存块的起始地址！
起始地址计算： J号内存块的起始地址=J*内存块大小

假设通过查询页表得知1号页面存放的内存块号是9（1001），
则9号内存块的起始地址=9X4096=00000000000000001001000000000000
则逻辑地址4097对应的物理地址=页面在内存中存放的起始地址+页内偏移量 =（00000000000000000011000000000001）

结论：如果页面大小刚好是2 的整数幂，则只需把页表中记录的物理块号拼接上页内偏移量就能得到对应的物理地址

1.3 基本地址变换机构

1. 基本地址变换机构可以借助进程的页表将逻辑地址转换为物理地址。
2. 通常会在系统中设置一个页表寄存器（PTR），存放页表在内存中的起始地址F和页表长度M。
3. 进程未执行时，页表的始址和页表长度放在进程控制块（PCB）中，当进程被调度时，操作系统内核会把它们放到页表寄存器中。

注意：页面大小是2的整数幂

设页面大小为L，逻辑地址A到物理地址E的变换过程如下：

变换过程说明：

1. 计算页号P和页内偏移量W（十进制手算：P=A/L，W=A%L；但是在计算机实际运行时，逻辑地址结构固定不变，因此计算机硬件可以更快地得到二进制表示的页号、页内偏移量）
2. 比较页号P和页表长度M，若P>=M，则产生越界中断，否则继续执行
   （注意：页号从0开始，而页表长度至少是1，因此P=M时也会越界）
3. 页表中页号P对应的页表项地址=页表起始地址F+页号P*页表项长度，取出改页表项内容b，即为内存块号。
   注意区分页表项长度、页表长度、页面大小的区别、页表长度指的是这个页表中总共有几个页表项，即总共有几个页；页表项长度指的是每个页表项占多大存储空间；页面大小指的是一个页面占多大的存储空间
4. 计算E=b*L+W，用得到的物理地址E去访存。（如果内存块号、页面偏移量是用二进制表示的，那么把二者拼接起来就是最终的物理地址了）

例：若页面大小L为1K字节，页号2对应的内存块号b=8，将逻辑地址A=2500转换为物理地址E。

题目等价描述：某系统按字节寻址，逻辑地址结构中，页内偏移量占10位，页号2对应的内存块号b=8，将逻辑地址A=2500转换为物理地址E。
页内偏移量占10位，说明一个页面的大小L为2¹⁰B=1KB

1. 计算页号、页内偏移量
   页号P=A/L=2500/1024=2；页内偏移量W=A%L=2500%1024=452
2. 根据题中条件可知，页号2没有越界，其存放的内存块号b=8
3. 物理地址E=b*L+W=8X1024+452=8644

在分页存储管理（页式管理）的系统中，只要确定了每个页面的大小，逻辑地址结构就确定了。因此，页式管理中地址是一维的。即只要给出一个逻辑地址，系统就可以自动地算出页号、页内偏移量两个部分，并不需要显式地告诉系统这个逻辑地址中，页内偏移量占多少位。

1.4 具有快表的地址变换机构

快表的地址变换机构：是基本地址变换机构的改进版本

1.4.1 什么是快表（TLB）

快表，又称联想寄存器（TLB，translation lookaside buffer ），是一种访问速度比内存快很多的高速缓存（TLB不是内存！），用来存放近访问的页表项的副本，可以加速地址变换的速度。 与此对应，内存中的页表常称为慢表。

1.4.2 引入快表后，地址的变换过程

1. CPU给出逻辑地址，由某个硬件算得页号、页内偏移量，将页号与快表中的所有页号进行比较。
2. 如果找到匹配的页号，说明要访问的页表项在快表中有副本，则直接从中取出该页对应的内存块号，再将内存块号与页内偏移量拼接形成物理地址，然后访问该物理地址对应的内存单元。因此， 若快表命中，则访问某个逻辑地址仅需一次访问内存即可。
3. 如果没有找到匹配的页号，则需要访问内存中的页表，找到对应页表项，得到页面存放的内存块号，再将内存块号与页内偏移量拼接形成物理地址，然后访问该物理地址对应的内存单元。因此， 若快表未命中，则访问某个逻辑地址需要两次访存
   （注意：在找到页表项后，应同时将其存入快表， 以便后面可能的再次访问。但若快表已满，则必须按照一定的算法对旧的页表项进行替换）

由于查询快表的速度比查询页表的速度快很多，因此只要快表命中，就可以节省很多时间。 因为局部性原理，一般来说快表的命中率可以达到90%以上。

• 例：某系统使用基本分页存储管理，并采用了具有快表的地址变换机构。访问一次快表耗时1us，访问一次内存耗时100us。若快表的命中率为90%，那么访问一个逻辑地址的平均耗时是多少？

(1+100)* 0.9+(1+100+100)* 0.1=111us

说明：

1. (1+100)* 0.9 访问逻辑地址，首先优先根据页号查询快表，耗时1us，若快表命中，就可以得到逻辑地址对应的最终的物理地址，再访问一次内存，就是访问我们最终要访问的物理单元，所以命中耗时101us；
2. 若快表未命中，需要访问内存，查询慢表，最后就可以得到逻辑地址对应的最终的物理地址，再访问一次内存，就是访问我们最终要访问的物理单元，所以未命中耗时201us；
3. 不管命中否，首先都得访问一次快表；
4. 本题是优先查询快表。

• 有的系统支持快表和慢表同时查找，如果是这样，平均耗时应该是(1+100)* 0.9+(100+100)* 0.1= 110.9us 若未采用快表机制，则访问一个逻辑地址需要100+100=200us 显然，引入快表机制后，访问一个逻辑地址的速度快多了。

1.4.3 地址变换过程小结

TLB和普通Cache的区别：

TLB中只有页表项的副本，而普通Cache中可能会有其他各种数据的副本

1.5 两级页表

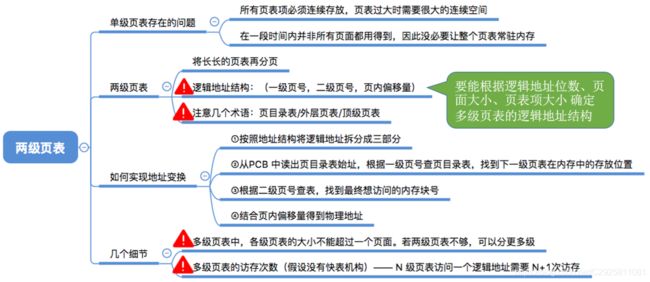
1.5.1 单级页表存在的问题，为啥引入两极页表

单级页表：

某计算机系统按字节寻址，支持32位的逻辑地址，采用分页存储管理，页面大小为4KB，页表项长度为4B。
4KB=2¹²B，因此页内地址要用12位表示，剩余20位表示页号。
因此，该系统中用户进程最多有2²⁰ 页。相应的，一个进程的页表中，最多会有2²⁰ =1M=1048576个页表项，所以一个页表最大需要 2²⁰ * 4B=2²² B，共需要2²² /2¹² =2¹⁰ 个页框存储该页表。
根据页号查询页表的方法：K号页对应的页表项存放位置=页表始址+K* 4
要在所有的页表项都连续存放的基础上才能用这种方法找到页表项

根据局部性原理可知，很多时候，进程在一段时间内只需要访问某几个页面就可以正常运行了。因此没有必要让整个页表都常驻内存。

思考：我们是如何解决进程在内存中必须连续存储的问题的？
将进程地址空间分页，并为其建立一张页表，记录各页面的存放位置同样的思路也可用于解决“页表必须连续存放”的问题，把必须连续存放的页表再分页，从而将页表拆开

把页表再分页并离散存储，然后再建立一张页表记录页表各个部分的存放位置，称为页目录表，或称外层页表，或称顶层页表

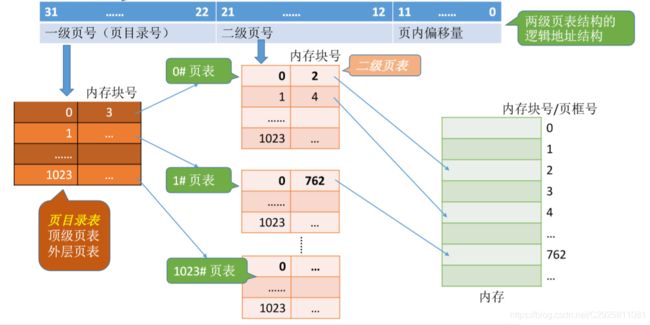
1.5.2 两级页表的原理、地址结构

1. 32位逻辑地址空间，页表项大小为4B，页面大小为4KB，则页内地址占12位 ，采用单级页表：
   
   因此，该系统中用户进程最多有2²⁰ 页。相应的，一个进程的页表中，最多会有2²⁰ =1M=1048576个页表项，所以一个页表最大需要 2²⁰ * 4B=2²² B，共需要2²² /2¹² =2¹⁰ 个页框存储该页表。
   

2. 现在把页表再分页并离散存储，然后再建立一张页表记录页表各个部分的存放位置，称为页目录表，或称外层页表，或称顶层页表
   

10位一级页号刚好可表示0~1023

1.5.3 二级页表如何实现地址变换

例：将逻辑地址(0000000000,0000000001,111111111111)转换为物理地址（用十进制表示）。

1. 按照地址结构将逻辑地址拆分成三部分
2. 从PCB中读出页目录表始址，再根据一级页号查页目录表，找到下一级页表在内存中的存放位置
3. 根据二级页号查二级页表，找到最终想访问的内存块号
4. 结合页内偏移量得到物理地址
   

最终要访问的内存块号为4
该内存块的起始地址为4*4096=16384
页内偏移量为4095
最终的物理地址为 16384+4095=20479

没有必要让整个页表常驻内存，因为进程在一段时间内可能只需要访问某几个特定的页面。

可以在需要访问页面时才把页面调入内存（虚拟存储技术）。可以 在页表项中增加一个标志位，用于表示该页面是否已经调入内存

1. 若分为两级页表后，页表依然很长，则可以采用更多级页表，一般来说各级页表的大小不能超过一个页面
   例：某系统按字节编址，采用40位逻辑地址，页面大小为4KB，页表项大小为4B，假设采用纯页式 存储，则要采用（）级页表，页内偏移量为（）位？

页面大小= 4KB =2¹²B，按字节编址，因此页内偏移量为12位
页号= 40-12 = 28位
页面大小= 2¹²B，页表项大小= 4B ，则每个页面可存放2¹² / 4 = 2¹⁰个页表项
因此各级页表最多包含2¹⁰个页表项，需要10 位二进制位才能映射到2¹⁰个页表项，因此每一级的页表对应页号应为10位。总共28位的页号至少要分为三级

如果只分为两级页表，则一级页号占18位， 也就是说页目录表中最多可能有2¹⁸个页表项，超过了一个页面， 显然，一个页面是放不下这么多页表项的

2. 两级页表的访存次数分析（假设没有快表机构）

第一次访存：访问内存中的页目录表
第二次访存：访问内存中的二级页表
第三次访存：访问目标内存单元

N级页表访问一个逻辑地址，需要N+1次访存

1.5.4 二级页表小结

2 基本分段存储管理方式

“分段”与“分页”最大的区别就是——离散分配时所分配地址空间的基本单位不同

2.1 分段

1. 进程的地址空间：按照程序自身的逻辑关系划分为若干个段，每个段都有一个段名（在低级语言中，程序员使用段名来编程），每段从0开始编址
2. 内存分配规则：以段为单位进行分配，每个段在内存中占据连续空间，但各段之间可以不相邻。

编译程序会 将段名转换为段号
由于是按逻辑功能模块划分，用户编程更方便，程序的可读性更高

LOAD1,[D]|<A>; //将分段D中A单元内的值读入寄存器1 
STORE1,[X]|<B>; //将寄存器1的内容存入X分段的B单元中

上述汇编指令，写程序时使用的段名[D]、[X]会被编译程序翻译成对应段号
单元、单元会被编译程序 翻译成段内地址

分段系统的逻辑地址结构由段号（段名）和段内地址（段内偏移量）所组成。如：

段号的位数决定了每个进程最多可以分几个段
段内地址位数决定了每个段的最大长度是多少

在上述例子中，若系统是按字节寻址的，则段号占16位，因此在该系统中，每个进程最多有2¹⁶ =64K个段； 段内地址占16位，因此每个段的最大长度是2¹⁶ =64KB。

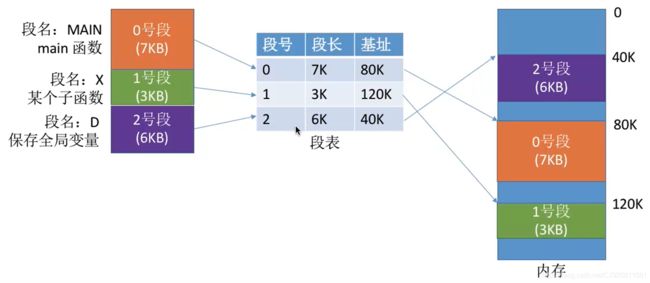
2.2 段表

问题：程序分多个段，各段离散地装入内存，为了保证程序能正常运行，就必须能从物理内存中找到各个逻辑段的存放位置。为此，需为每个进程建立一张段映射表，简称“段表”。

1. 每个段对应一个段表项，其中记录了该段在内存中的起始位置（又称 “基址”）和段的长度。
2. 各个段表项的长度是相同的。

例如：某系统按字节寻址，采用分段存储管理，逻辑地址结构为（段号16位,段内地址16位），因此用16位即可表示最大段长。物理内存大小为4GB（可用32位表示整个物理内存地址空间）。
因此，可以让每个段表项占16+32=48位，即6B。由于段表项长度相同，因此段号可以是隐含的，不占存储空间。
若段表存放的起始地址为M，则K号段对应的段表项存放的地址为M+K*6

2.3 地址变换

2.4 分段、分页管理的对比

1. 页是信息的物理单位。分页的主要目的是为了实现离散分配，提高内存利用率。分页仅仅是系统管理上的需要，完全是系统行为，对用户是不可见的。
   段是信息的逻辑单位。分段的主要目的是更好地满足用户需求。一个段通常包含着一组属于一个逻辑模块的信息。分段对用户是可见的，用户编程时需要显式地给出段名。

2. 页的大小固定且由系统决定。
   段的长度却不固定，决定于用户编写的程序。

3. 分页的用户进程地址空间是一维的，程序员只需给出一个记忆符即可表示一个地址。
   分段的用户进程地址空间是二维的，程序员在标识一个地址时，既要给出段名，也要给出段内地址。

4. 分段比分页更容易实现信息的共享和保护。
   不能被修改的代码称为纯代码或可重入代码（不属于临界资源），这样的代码是可以共享的。可修改的代码是不能共享的（比如，有一个代码段中有很多变量，各进程并发地同时访问可能造成数据不一致）

只需让各进程的段表项指向同一个段即可实现共享

5. 访问一个逻辑地址需要几次访存？
   （1）分页（单级页表）：第一次访存——查内存中的页表，第二次访存——访问目标内存单元。总共两次访存
   （2）分段：第一次访存——查内存中的段表，第二次访存——访问目标内存单元。总共两次访存
   （3）与分页系统类似，分段系统中也可以引入快表机构，将近期访问过的段表项放到快表中，这样可以少一次访问，加快地址变换速度。

2.5 分段存储管理小结

3 段页式存储管理

3.1 分页、分段优缺点分析

分段管理中产生的外部碎片也可以用“紧凑”来解决，只是需要付出较大的时间代价

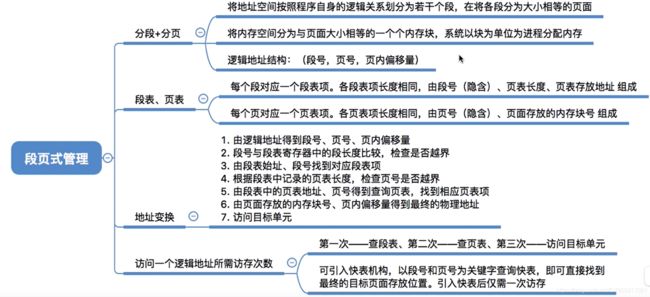
3.2 分段+分页=段页式管理

3.3 段页式管理的逻辑地址结构

即把段内地址再拆分为页号+页面偏移量
段号的位数决定了每个进程最多可以分几个段
页号位数决定了每个段最大有多少页
页内偏移量决定了页面大小、内存块大小是多少

在上述例子中，若系统是按字节寻址，则

• 段号占16位，因此在该系统中，每个进程最多有2¹⁶=64K个字段
• 页号占4位，因此每个段最多有2⁴=16页
• 页内偏移量占12位，因此每个页面\每个内存块大小为2¹²=4096=4KB

“分段”对用户是可见的，程序员编程时需要显式地给出段号、段内地址。
而将各段“分页”对用户是不可见的。系统会根据段内地址自动划分页号和页内偏移量。
因此段页式管理的地址结构是二维的。

简记：页式一维、段式二维、段页式二维

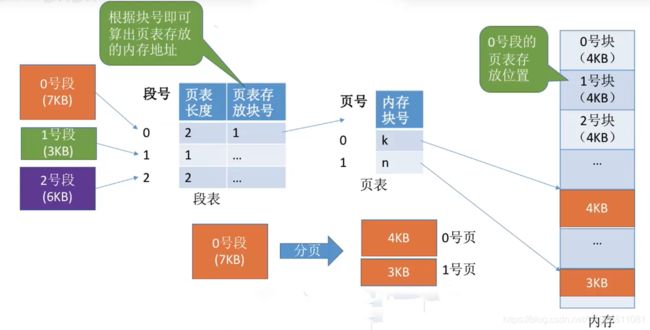
3.4 段表、页表

每个段对应一个段表项，每个段表项由段号、页表长度、页表存放块号（页表起始地址）组成。每个段表项长度相等，段号是隐含的。

每个页面对应一个页表项，每个页表项由页号、页面存放的内存块号组成。每个页表项长度相等，页号是隐含的。

3.5 段页式管理地址变换过程

也可引入快表机构，用段号和页号作为查询快表的关键字。若快表命中则仅需一次访存

3.6 段页式管理小结