《视觉 SLAM 十四讲》V2 第 12 讲 建图
文章目录
-
- 12.2 单目稠密 重建
-
- 12.2.2 极线搜索 && 块匹配
- 12.2.3 高斯分布的深度滤波器
- 12.3 单目稠密重建 【Code】
-
- 待改进
- 12.3.4 图像间的变换
- 12.4 RGB-D 稠密建图
-
- 12.4.1 点云地图 【Code】
-
-
-
- 查询OpenCV版本 opencv_version
-
-
- 12.4.2 从点云 重建 网格 【Code】
-
-
-
- 查看PCL 版本 aptitude show libpcl-dev
-
-
- 12.4.3 八叉树地图(Octomap) 【灵活压缩、随时更新】
- 12.4.4 八叉树地图 【建模大场景】 【Code】
- 习题
-
- √ 题1
- √ 题2
- 题3
- 题4
- 题5
- 题6
单目SLAM 稠密 深度估计
单目 稠密 重建
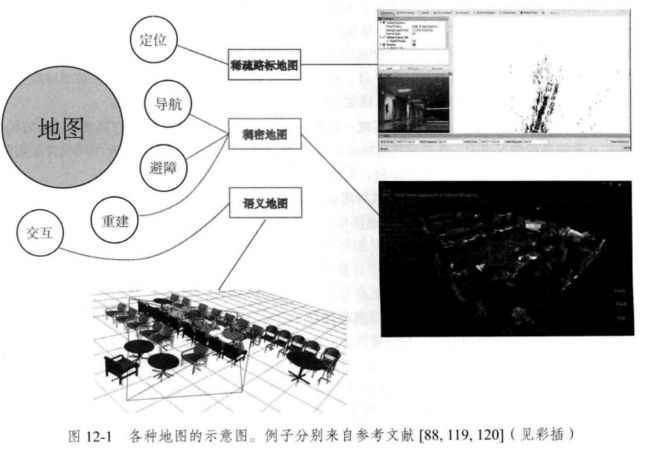
RGB-D 重建 的地图形式
估计 相机运动轨迹 + 特征点空间位置
机器人SLAM：定位、导航、避障和交互
SLAM： 同时定位 与 建图
经典 SLAM 地图(路标点的集合)
视觉里程计、BA： 建模了路标点的位置
扫地机: 全局定位，导航，路径规划
增强现实设备： 将虚拟物叠加在现实物体之中， 处理虚拟物体与真实物体之间的遮挡关系。
定位（空间位姿信息）： 把地图保存下来，这样只需对地图进行一次建模， 而不是每次启动机器人都重新做一次完整的SLAM
导航、避障：需要 稠密地图。哪些地方可通过
重建 三维视频通话、网上购物 纹理稠密
交互 语义地图
稀疏路标地图 只建模感兴趣部分 定位
稠密地图 建模 所有看到过的部分 导航避障
视觉SLAM 如何建 稠密地图
12.2 单目稠密 重建
获取像素点间距离的方法：
1、单目相机 三角化 计算像素之间的距离
2、双目相机， 利用左右目的视差 计算像素的距离
3、RGB-D相机 直接 获取 像素距离。
立体视觉(Stereo Vision)
移动单目相机 (移动视角的立体视觉(Moving View Stereo,MVS))
使用单目和双目 获取深度 费力不讨好。 计算量巨大、不可靠
场景： 室外，大场景
RGB-D： 量程、应用范围、光照限制。
极线搜索 块匹配
深度滤波技术 ：多次使用 三角测量法 让深度估计收敛。
12.2.2 极线搜索 && 块匹配
单个像素的亮度 没有区分性 ——> 比较 像素块。
计算两个小块之间的差异：
去均值 的 NCC
不断 对不同图像 进行极线 搜索时， 估计的深度分布将如何变化。
12.2.3 高斯分布的深度滤波器
均匀-高斯混合分布的滤波器
12.3 单目稠密重建 【Code】
mkdir build && cd build
cmake ..
make
./dense_mapping /home/xixi/Downloads/slambook2-master/ch12/semi_dense_mono/dataset/test_data
dense_mapping.cpp
#include CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(dense_monocular)
set(CMAKE_CXX_STANDARD 14)
set(CMAKE_BUILD_TYPE "Debug")
set(CMAKE_CXX_FLAGS "-std=c++17 -march=native -O3")
############### dependencies ######################
# Eigen
include_directories("/usr/include/eigen3")
# OpenCV
find_package(OpenCV 4.8.0 REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
# Sophus
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
set(THIRD_PARTY_LIBS
${OpenCV_LIBS}
${Sophus_LIBRARIES})
add_executable(dense_mapping dense_mapping.cpp)
target_link_libraries(dense_mapping ${THIRD_PARTY_LIBS})
待改进
12.3.2 像素梯度
块匹配的正确与否 依赖于 图像块是否具有区分度。
立体视觉的重建质量 依赖 环境纹理。
——————————
12.3.3 逆深度(深度的倒数)， 认为符合高斯分布。
12.3.4 图像间的变换
GPU 并行化 提高效率
极线搜索
其它改进：
1、给深度估计 加上 空间正则项
2、考虑错误匹配的情形: 均匀-高斯混合分布下的深度滤波器（显式地将内点与外点进行区别并进行概率建模）
————————
12.4 RGB-D 稠密建图
深度数据与纹理无关
根据估算的相机位姿，将RGB-D数据转化为点云，然后进行拼接。
12.4.1 点云地图 【Code】
点云： 一组离散的点表示的地图。
外点去除滤波器 体素网格的降采样滤波器(Voxel grid filter)
安装点云库
sudo apt-get install libpcl-dev pcl-tools
与第5讲的变化：
1、生成每帧点云时，去掉深度值无效的点。Kinect 的量程限制
2、利用统计滤波器去除孤立点。计算附近N个点距离的平均值，去除距离均值过大的点。
3、体素网格滤波器进行降采样。
要在CMakeLists.txt文件里加这一句，使得 支持C++14标准。 可能是最新版本的PCL 要求支持C++14标准。
set(CMAKE_CXX_STANDARD 14)
查询OpenCV版本 opencv_version
增加OpenCV的版本
所有.cpp中的文件路径都要改成..多回一级
pointcloud_mapping.cpp
#include CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
set(CMAKE_CXX_STANDARD 14)
set(CMAKE_BUILD_TYPE Release)
set(CMAKE_CXX_FLAGS "-std=c++11 -O2")
# opencv
find_package(OpenCV 4.8.0 REQUIRED) ## 改成 当前系统的OpenCV版本
include_directories(${OpenCV_INCLUDE_DIRS})
# eigen
include_directories("/usr/include/eigen3/")
# pcl
find_package(PCL 1.10.0 REQUIRED) #
include_directories(${PCL_INCLUDE_DIRS})
add_definitions(${PCL_DEFINITIONS})
# octomap
find_package(octomap REQUIRED)
include_directories(${OCTOMAP_INCLUDE_DIRS})
add_executable(pointcloud_mapping pointcloud_mapping.cpp)
target_link_libraries(pointcloud_mapping ${OpenCV_LIBS} ${PCL_LIBRARIES})
add_executable(octomap_mapping octomap_mapping.cpp)
target_link_libraries(octomap_mapping ${OpenCV_LIBS} ${PCL_LIBRARIES} ${OCTOMAP_LIBRARIES})
add_executable(surfel_mapping surfel_mapping.cpp)
target_link_libraries(surfel_mapping ${OpenCV_LIBS} ${PCL_LIBRARIES})
mkdir build && cd build ## 需要将.cpp中数据的路径 多加一个.
cmake ..
make
./pointcloud_mapping
pcl_viewer map.pcd
体素滤波之后的点云：
12.4.2 从点云 重建 网格 【Code】
./surfel_mapping map.pcd
点云转换成 网格地图(栅格地图)。
surfel_mapping.cpp
//
// Created by gaoxiang on 19-4-25.
//
#include 重建算法： Moving Least Square 、 Greedy Projection
查看PCL 版本 aptitude show libpcl-dev
aptitude show libpcl-dev
可参考链接
12.4.3 八叉树地图(Octomap) 【灵活压缩、随时更新】
点云地图 不足：
1、占内存，提供了很多不必要的细节
2、无法处理运动物体。 只有 “添加点”，点消失时 不会 被移除。
八叉树 比 点云 节省大量的存储空间
- 当某个方块的所有子结点都被占据或都不被占据时，就没必要展开。
12.4.4 八叉树地图 【建模大场景】 【Code】
安装 octomap库
sudo apt-get install liboctomap-dev octovis
./octomap_mapping
octovis octomap.bt
动图截取：
byzanz-record -x 72 -y 64 -w 1848 -h 893 -d 10 --delay=5 -c /home/xixi/myGIF/test.gif
octomap_mapping.cpp
#include ——————————
12.5 TSDF 地图 和 Fusion系列
TSDF(Truncated Signed Distance Function，截断符号距离函数)
实时三维重建： 重建准确地图
定位算法 可以满足实时性需求，地图加工可在关键帧处进行处理，无需实时。
SLAM 轻量级、小型化
实时三维重建 大规模、大型动态场景。
——————————
12.6 小结
度量地图
RGB-D 构建稠密地图 更容易、更稳定一些
习题
√ 题1
#*********************************解题1开始
设某个像素点的深度 d d d 服从高斯分布 P ( d ) = N ( μ , σ 2 ) P(d) = N(\mu, σ^2) P(d)=N(μ,σ2)
增加新数据后，重新观测到的深度分布符合高斯分布 P ( d o b s ) = N ( μ o b s , σ o b s 2 ) P(d_{obs}) = N(\mu_{obs}, σ_{obs}^2) P(dobs)=N(μobs,σobs2)
信息融合后的深度为这两个高斯分布的乘积，即
P ( d f u s e ) = N ( μ , σ 2 ) ⋅ N ( μ o b s , σ o b s 2 ) = 1 2 π σ e x p ( − 1 2 ( x − μ ) 2 σ 2 ) ⋅ 1 2 π σ o b s e x p ( − 1 2 ( x − μ o b s ) 2 σ o b s 2 ) = 1 2 π σ σ o b s e x p ( − 1 2 ( x − μ ) 2 σ 2 − 1 2 ( x − μ o b s ) 2 σ o b s 2 ) = 1 2 π σ σ o b s e x p ( − 1 2 σ o b s 2 ⋅ ( x − μ ) 2 + σ 2 ⋅ ( x − μ o b s ) 2 σ 2 σ o b s 2 ) = 1 2 π σ σ o b s e x p ( − 1 2 ( σ o b s 2 + σ 2 ) ⋅ x 2 − 2 ( σ o b s 2 μ + σ 2 μ o b s ) ⋅ x + σ o b s 2 μ 2 + σ 2 μ o b s 2 σ 2 σ o b s 2 ) = 1 2 π σ σ o b s e x p ( − 1 2 x 2 − 2 σ o b s 2 μ + σ 2 μ o b s σ o b s 2 + σ 2 ⋅ x + σ o b s 2 μ 2 + σ 2 μ o b s 2 σ o b s 2 + σ 2 σ 2 σ o b s 2 σ o b s 2 + σ 2 ) = 1 2 π σ σ o b s e x p ( − 1 2 ( x − σ o b s 2 μ + σ 2 μ o b s σ o b s 2 + σ 2 ) 2 σ 2 σ o b s 2 σ o b s 2 + σ 2 ) ⋅ e x p ( − 1 2 σ o b s 2 μ 2 + σ 2 μ o b s 2 σ o b s 2 + σ 2 − ( σ o b s 2 μ + σ 2 μ o b s σ o b s 2 + σ 2 ) 2 σ 2 σ o b s 2 σ o b s 2 + σ 2 ) = 1 2 π σ σ o b s σ o b s 2 + σ 2 e x p ( − 1 2 ( x − σ o b s 2 μ + σ 2 μ o b s σ o b s 2 + σ 2 ) 2 σ 2 σ o b s 2 σ o b s 2 + σ 2 ) ⋅ e x p ( − 1 2 σ o b s 2 μ 2 + σ 2 μ o b s 2 σ o b s 2 + σ 2 − ( σ o b s 2 μ + σ 2 μ o b s σ o b s 2 + σ 2 ) 2 σ 2 σ o b s 2 σ o b s 2 + σ 2 ) 2 π σ o b s 2 + σ 2 \begin{align*}P(d_{fuse}) &= N(\mu, σ^2) ·N(\mu_{obs}, σ_{obs}^2) \\ & = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}) · \frac{1}{\sqrt{2\pi}\sigma_{obs}}exp(-\frac{1}{2}\frac{(x-\mu_{obs})^2}{\sigma_{obs}^2}) \\ &= \frac{1}{2\pi\sigma\sigma_{obs}}exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2}-\frac{1}{2}\frac{(x-\mu_{obs})^2}{\sigma_{obs}^2})\\ &= \frac{1}{2\pi\sigma\sigma_{obs}}exp(-\frac{1}{2}\frac{\sigma_{obs}^2·(x-\mu)^2+\sigma^2·(x-\mu_{obs})^2}{\sigma^2\sigma_{obs}^2})\\ &= \frac{1}{2\pi\sigma\sigma_{obs}}exp(-\frac{1}{2}\frac{(\sigma_{obs}^2+\sigma^2)·x^2-2(\sigma_{obs}^2\mu+\sigma^2\mu_{obs})·x+\sigma_{obs}^2\mu^2+\sigma^2\mu_{obs}^2}{\sigma^2\sigma_{obs}^2})\\ &= \frac{1}{2\pi\sigma\sigma_{obs}}exp(-\frac{1}{2}\frac{x^2-2\frac{\sigma_{obs}^2\mu+\sigma^2\mu_{obs}}{\sigma_{obs}^2+\sigma^2}·x+\frac{\sigma_{obs}^2\mu^2+\sigma^2\mu_{obs}^2}{\sigma_{obs}^2+\sigma^2}}{\frac{\sigma^2\sigma_{obs}^2}{\sigma_{obs}^2+\sigma^2}})\\ &= \frac{1}{2\pi\sigma\sigma_{obs}}exp(-\frac{1}{2}\frac{(x-\frac{\sigma_{obs}^2\mu+\sigma^2\mu_{obs}}{\sigma_{obs}^2+\sigma^2})^2}{\frac{\sigma^2\sigma_{obs}^2}{\sigma_{obs}^2+\sigma^2}})·exp(-\frac{1}{2}\frac{\frac{\sigma_{obs}^2\mu^2+\sigma^2\mu_{obs}^2}{\sigma_{obs}^2+\sigma^2}-(\frac{\sigma_{obs}^2\mu+\sigma^2\mu_{obs}}{\sigma_{obs}^2+\sigma^2})^2}{\frac{\sigma^2\sigma_{obs}^2}{\sigma_{obs}^2+\sigma^2}})\\ &= \frac{1}{\sqrt{2\pi}\frac{\sigma\sigma_{obs}}{\sqrt{\sigma_{obs}^2+\sigma^2}}}exp(-\frac{1}{2}\frac{(x-\frac{\sigma_{obs}^2\mu+\sigma^2\mu_{obs}}{\sigma_{obs}^2+\sigma^2})^2}{\frac{\sigma^2\sigma_{obs}^2}{\sigma_{obs}^2+\sigma^2}})·\frac{exp(-\frac{1}{2}\frac{\frac{\sigma_{obs}^2\mu^2+\sigma^2\mu_{obs}^2}{\sigma_{obs}^2+\sigma^2}-(\frac{\sigma_{obs}^2\mu+\sigma^2\mu_{obs}}{\sigma_{obs}^2+\sigma^2})^2}{\frac{\sigma^2\sigma_{obs}^2}{\sigma_{obs}^2+\sigma^2}})}{\sqrt{2\pi}\sqrt{\sigma_{obs}^2+\sigma^2}}\\ \end{align*} P(dfuse)=N(μ,σ2)⋅N(μobs,σobs2)=2πσ1exp(−21σ2(x−μ)2)⋅2πσobs1exp(−21σobs2(x−μobs)2)=2πσσobs1exp(−21σ2(x−μ)2−21σobs2(x−μobs)2)=2πσσobs1exp(−21σ2σobs2σobs2⋅(x−μ)2+σ2⋅(x−μobs)2)=2πσσobs1exp(−21σ2σobs2(σobs2+σ2)⋅x2−2(σobs2μ+σ2μobs)⋅x+σobs2μ2+σ2μobs2)=2πσσobs1exp(−21σobs2+σ2σ2σobs2x2−2σobs2+σ2σobs2μ+σ2μobs⋅x+σobs2+σ2σobs2μ2+σ2μobs2)=2πσσobs1exp(−21σobs2+σ2σ2σobs2(x−σobs2+σ2σobs2μ+σ2μobs)2)⋅exp(−21σobs2+σ2σ2σobs2σobs2+σ2σobs2μ2+σ2μobs2−(σobs2+σ2σobs2μ+σ2μobs)2)=2πσobs2+σ2σσobs1exp(−21σobs2+σ2σ2σobs2(x−σobs2+σ2σobs2μ+σ2μobs)2)⋅2πσobs2+σ2exp(−21σobs2+σ2σ2σobs2σobs2+σ2σobs2μ2+σ2μobs2−(σobs2+σ2σobs2μ+σ2μobs)2)
显然，前面部分符合高斯分布 N ( μ f u s e , σ f u s e 2 ) N(\mu_{fuse}, σ_{fuse}^2) N(μfuse,σfuse2)，其中
μ f u s e = σ o b s 2 μ + σ 2 μ o b s σ o b s 2 + σ 2 , , , σ f u s e 2 = σ 2 σ o b s 2 σ o b s 2 + σ 2 \mu_{fuse} = \frac{\sigma_{obs}^2\mu+\sigma^2\mu_{obs}}{\sigma_{obs}^2+\sigma^2}, ,, σ_{fuse}^2=\frac{\sigma^2\sigma_{obs}^2}{\sigma_{obs}^2+\sigma^2} μfuse=σobs2+σ2σobs2μ+σ2μobs,,,σfuse2=σobs2+σ2σ2σobs2
后面部分为 常数，不影响其高斯分布类型
关于这个常数的补充说明如下，供参考
import numpy as np
import matplotlib.pyplot as plt
# 绘制高斯分布曲线
x = np.linspace(-4, 4, 100)
y = gaussian.pdf(x)
plt.plot(x, 0.2*y, 'orange')
plt.plot(x, y, 'r')
plt.plot(x, 2*y, 'b')
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Gaussian Distribution')
plt.show()
正态分布的数学期望值或期望值 μ μ μ 等于位置参数，决定了分布的位置；其方差 σ 2 \sigma ^{2} σ2 等于尺度参数，决定了分布的幅度。
#*********************************解题1结束
√ 题2
半稠密深度估计，先把梯度明显的地方筛选出来。
数据集下载链接： https://rpg.ifi.uzh.ch/datasets/remode_test_data.zip
在 update 函数部分添加梯度比较和筛选代码。
#*********************************解题2开始
建 空白文件
touch CMakeLists.txt
touch semi_dense_mapping.cpp
复制相应的代码
报错：
/home/xixi/Downloads/slambook2-master/ch12/dense_mono/dense_mapping.cpp:12:15: error: ‘Sophus::SE3d’ has not been declared
12 | using Sophus::SE3d;
解决办法链接
报错原因：没将 update函数的类型改为 void
mkdir build && cd build
cmake ..
make
./semi_dense_mapping /home/xixi/Downloads/slambook2-master/ch12/semi_dense_mono/dataset/test_data
CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(semi_dense_monocular)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-std=c++11 -march=native -O3")
############### dependencies ######################
# Eigen
include_directories("/usr/include/eigen3")
# OpenCV
find_package(OpenCV 4 REQUIRED) ## OpenCV是4.8.0 .cpp文件需要修改
include_directories(${OpenCV_INCLUDE_DIRS})
# Sophus
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
set(THIRD_PARTY_LIBS
${OpenCV_LIBS}
${Sophus_LIBRARIES})
add_executable(semi_dense_mapping semi_dense_mapping.cpp)
target_link_libraries(semi_dense_mapping ${THIRD_PARTY_LIBS})
semi_dense_mapping.cpp
#include #*********************************解题2结束
题3
3、单目稠密重建从正深度 改成 逆深度，并添加仿射变换。
仿射变换用于 块匹配前，进一步考虑了相机发生运动的情形（当前帧和参考帧之间发行运动了），以期可以取得更好的 匹配效果。
实际的深度分布： 尾部稍长，负数区域为0 逆深度
ORB_SLAM2
题4
4、论证如何在八叉树中进行导航和路径规划
navigation based on octomap
导航navigation
localization定位
mapping建图
planning路径规划
SLAM
导航：如何从地图中A点到B点。
- 如何在地图中地位自己（localization）
- 如何从 A 到 B 规划一条路径（planning）， path planning 有global和local之分，同时都需要。global path planning有dijkstra，A* ，D*等算法。local path planning 有自适应动态窗法等。
Autonomous Navigation in Unknown Environments with Sparse Bayesian Kernel-based Occupancy Mapping
OctoMap:An Efficient Probabilistic 3D Mapping Framework Based on Octrees
找到了别的树
FAST-LIO2: Fast Direct LiDAR-inertial Odometry
题5
5、TSDF是如何进行位姿估计和更新的。
论文链接： KinectFusion: Real-Time Dense Surface Mapping and Tracking
题6
6、均匀-高斯混合滤波器的原理与实现
待做：
- 用数据集 跑源码
在12.2.3 节讨论了。P311
SVO源码链接
PDF链接：https://rpg.ifi.uzh.ch/docs/ICRA14_Forster.pdf
SVO 全称 Semi-direct monocular Visual Odometry（半直接视觉里程计)
点云 深度 概率模型是 高斯+均匀分布
瑞士苏黎世大学 机器人与感知小组http://rpg.ifi.uzh.ch。
https://github.com/uzh-rpg/rpg_svo/blob/master/svo/src/depth_filter.cpp
其它：
SVO的深度滤波器使用的概率模型是《Video-based, Real-Time Multi View Stereo》中的深度概率模型，不同的是SVO中的使用的逆深度估计。
Video-based, Real-Time Multi View Stereo》pdf链接