深度学习——稠密连接网络（DenseNet）

深度学习——稠密连接网络（DenseNet）

---

前言

上篇文章，学习了残差网络，ResNet极大地改变了如何参数化深层网络中函数的观点。 而稠密连接网络（DenseNet） 在某种程度上是ResNet的逻辑扩展。

---

一、从ResNet到DenseNet

回想一下任意函数的泰勒展开式，它把这个函数分解成越来越高阶的项。

f(x) = f(a) + f’(a)(x-a) + f’‘(a)(x-a)^2/2! + f’‘’(a)(x-a)^3/3! + …

在$x$接近0时：

$$f(x)=f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\frac{f^{\prime \prime \prime }(0)}{3!}{x}^3+\dots .$$

同样，ResNet将函数展开为

$$f(\mathbf{x})=\mathbf{x}+g(\mathbf{x}).$$

也就是说，ResNet将$f$分解为两部分：一个简单的线性项和一个复杂的非线性项。

那么再向前拓展一步，如果我们想将$f$拓展成超过两部分的信息呢？一种方案便是DenseNet。

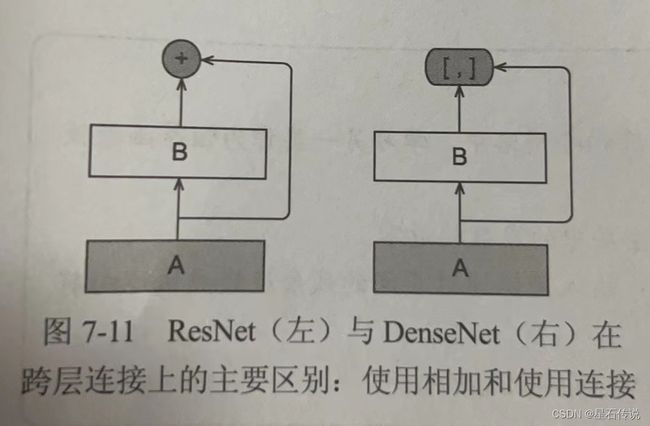
如图所示，ResNet和DenseNet的关键区别在于，DenseNet输出是连接（用图中的$[,]$表示）而不是如ResNet的简单相加。

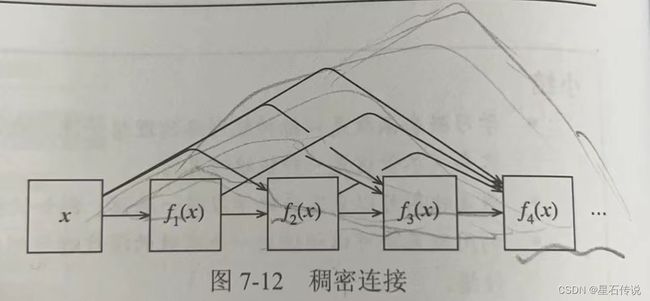
因此，在应用越来越复杂的函数序列后，我们执行从$\mathbf{x}$到其展开式的映射：

$$\mathbf{x}\to \left[\mathbf{x},f_1(\mathbf{x}),f_2([\mathbf{x},f_1(\mathbf{x})]),f_3([\mathbf{x},f_1(\mathbf{x}),f_2([\mathbf{x},f_1(\mathbf{x})])]),\dots \right].$$

最后，将这些展开式结合到多层感知机中，再次减少特征的数量（只要将它们连接起来）。

DenseNet这个名字由变量之间的“稠密连接”而得来，最后一层与之前的所有层紧密相连。稠密连接如下图所示。

稠密网络主要由2部分构成：稠密块（dense block）和过渡层（transition layer）。
前者定义如何连接输入和输出，而后者则控制通道数量，使其不会太复杂。

二、稠密块体

DenseNet使用了ResNet改良版的“批量规范化、激活和卷积”架构，我们首先实现一下这个架构。

def conv_block(input_channels,num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels),nn.ReLU(),
        nn.Conv2d(input_channels,num_channels,kernel_size=3,padding=1)
    )

一个稠密块由多个卷积块组成，每个卷积块使用相同数量的输出通道。
然而，在前向传播中，我们将每个卷积块的输入和输出在通道维上连结。

class DenseBlock(nn.Module):
    def __init__(self,num_convs,input_channels,num_channels):
        super(DenseBlock,self).__init__()
        layer =[]
        for i in range(num_convs):
            layer.append(conv_block(num_channels*i+input_channels,num_channels))
        self.net = nn.Sequential(*layer)
    def forward(self,X):
        for blk in self.net:
            Y = blk(X)
            #连接通道维度上每个卷积块的输入和输出
            X = torch.cat((X,Y),dim=1)
        return X

#定义一个有2个输出通道数为10的(DenseBlock)。 使用通道数为3的输入时，我们会得到通道数为3+2×10=23的输出。
# 卷积块的通道数控制了输出通道数相对于输入通道数的增长，因此也被称为增长率（growth rate）。

blk = DenseBlock(2, 3, 10)
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
print(Y.shape)

三、过渡层

由于每个稠密块都会带来通道数的增加，使用过多则会过于复杂化模型。
而过渡层可以用来控制模型复杂度。 它通过1×1卷积层来减小通道数，
并使用步幅为2的平均汇聚层减半高和宽，从而进一步降低模型复杂度。

def transition_block(input_channels,num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels),nn.ReLU(),
        nn.Conv2d(input_channels,num_channels,kernel_size=1),
        nn.AvgPool2d(kernel_size=2,stride=2)
    )


blk = transition_block(23,10)
print(blk(Y).shape)

四、DenseNet模型

#DenseNet首先使用同ResNet一样的单卷积层和最大汇聚层。
b1 = nn.Sequential(
    nn.Conv2d(1,64,kernel_size=7,padding=3,stride=2),
    nn.BatchNorm2d(64),nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)


#在每个模块之间，ResNet通过步幅为2的残差块减小高和宽，DenseNet则使用过渡层来减半高和宽，并减半通道数。


#构建一个包含多个稠密块和转换层的网络结构，并返回一个包含这些稠密块和转换层的列表blks。
num_channels, growth_rate = 64, 32  #初始通道数和每个稠密块中的通道增长率
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs * growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2 #更新num_channels的值


#与ResNet类似，最后连接全局汇聚层和全连接层来输出结果
net = nn.Sequential(
    b1,*blks,
    nn.BatchNorm2d(num_channels),nn.ReLU(),
    nn.AdaptiveAvgPool2d((1,1)),nn.Flatten(),
    nn.Linear(num_channels,10)
)

五、模型训练

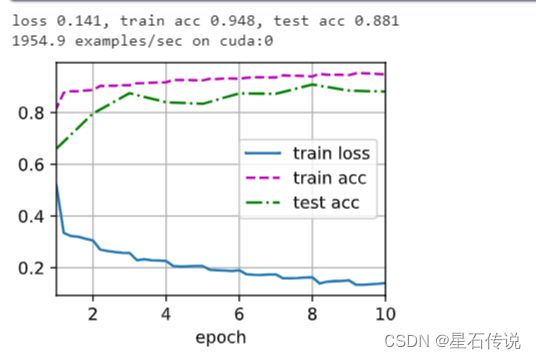
lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
d2l.plt.show()

---

总结

在跨层连接上，不同于ResNet中将输入与输出相加，DenseNet在通道维度上连接输入与输出。
DenseNet的主要构建模块是稠密块和过渡层，我们需要通过添加过渡层来控制网络的维数，从而再次减少通道的数量。

天之道，利而不害；圣人之道，为而不争

–2023-10-15 进阶篇