Linear、Logistic回归
线性回归
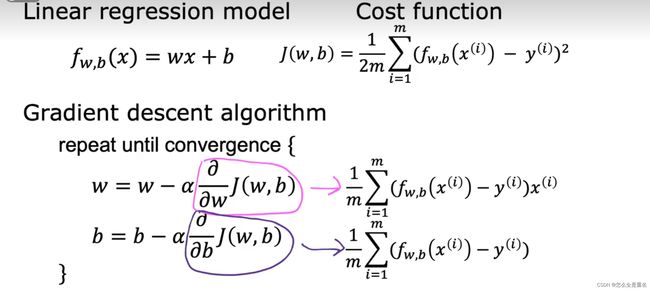
线性回归的目标是找到最佳拟合线,以使观测数据点与该线的残差(实际值与预测值之间的差异)最小化。线性回归通常用于探索变量之间的趋势、预测未来数值,或者用于发现因果关系。
简单实例(波士顿房价)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
#高版本scikit-sklearn中已经删除了该方法
#boston = datasets.load_boston() # 加载波士顿房子数据集
#print(boston.DESCR) # 查看数据描述
from sklearn.datasets import fetch_openml
boston = fetch_openml(name='boston', as_frame=True)
X = boston.data # 特征
y = boston.target # 标签
#plt.scatter(X[:,5],y) 可能版本问题,生成的是numpy数组但无效
# 从图中发现,房价超过50万的样本可能有异常
plt.scatter(X.iloc[:,5],y)
plt.show()
X = X[y<50.0] # 选择房价小于50万的样本特征
y = y[y<50.0] # 选择房价小于50万的样本标签
from sklearn.model_selection import train_test_split
# 依据chatgpt先进行标准化处理后拆分数据集
# 特征标准化处理
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
X = std.fit_transform(X)
# 拆分数据集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
#以下全省略
#std = StandardScaler()
# 对训练样本集进行特征标准化处理
#X_train_standard = std.fit_transform(X_train)
# 对测试样本集进行特征标准化处理,要注意这里不能fit了!
#X_test_standard = std.transform(X_test)
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
# 使用标准化后的训练样本集进行拟合学习(建立合适的线性回归模型)
lin_reg.fit(X_train_standard,y_train)
# 在测试集上测试模型的优劣,使用的是R^2标准
print(lin_reg.score(X_test_standard,y_test))
逻辑回归
Logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘、疾病自动诊断、经济预测等领域。逻辑回归从本质来说属于二分类问题。
二分类问题是指预测的y值只有两个取值(0或1)。例如:一个垃圾邮件过滤系统,x是邮件的特征,预测的y值就是邮件的类别(是垃圾邮件还是正常邮件)。
sigmoid函数
简单实例
import numpy as np
class LogisticRegression:
def __init__(self, learning_rate=0.01, num_iterations=1000):
self.learning_rate = learning_rate
self.num_iterations = num_iterations
def sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def fit(self, X, y):
m, n = X.shape
self.theta = np.zeros(n + 1)
X = np.column_stack((np.ones((m, 1)), X)) # 添加偏置项
for _ in range(self.num_iterations):
z = np.dot(X, self.theta)
h = self.sigmoid(z)
gradient = np.dot(X.T, (h - y)) / m
self.theta -= self.learning_rate * gradient
def predict(self, X):
X = np.column_stack((np.ones((X.shape[0], 1)), X))
z = np.dot(X, self.theta)
h = self.sigmoid(z)
predictions = (h >= 0.5).astype(int)
return predictions
if __name__ == "__main__":
# 示例数据集
X = np.array([[2.5, 3.5], [1.5, 2.5], [3.5, 4.5], [2.0, 2.5], [2.8, 2.8], [3.8, 3.0]])
y = np.array([1, 0, 1, 0, 1, 1])
# 创建并训练 logistic 回归模型
model = LogisticRegression(learning_rate=0.1, num_iterations=1000)
model.fit(X, y)
# 进行预测
new_data = np.array([[2.2, 2.9], [3.3, 3.7]])
predictions = model.predict(new_data)
print("预测结果:", predictions)

