LeetCode通关：哈希表六连，这个还真有点简单

哈希表基础

哈希表也叫散列表，哈希表是一种映射型的数据结构。

哈希表是根据关键码的值而直接进行访问的数据结构。

就好像老三和老三的工位：有人来找老三，前台小姐姐一指，那个像狗窝一样的就是老三的工位。

总体来说，散列表由两个要素构成：桶数组与散列函数。

桶及桶数组

散列表使用的桶数组（Bucket array ），其实就是一个容量为 N 的普通数组，只不过在这里，我们将其中的每个单元都想象为一个“桶”（Bucket），每个桶单元里都可以存放一个条目。

比如，所有的关键码都是整数，我们就可以直接将 key 为关键码的那个条目存放在桶单元 A[key]内；为了节省空间，空闲的单元都被置为 null。

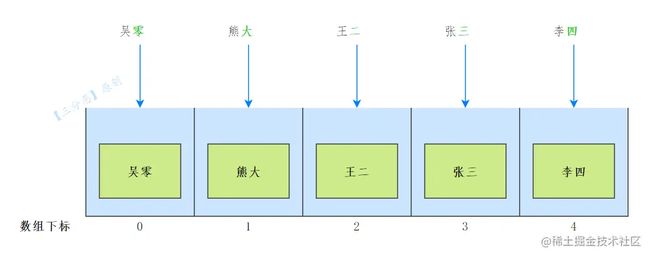
例如，吴零、熊大、王二、张三、李四，我们可以把他们放到桶数组对应的位置。

那么查找的时候，我们根据对应的名字编号，直接去找数组的下标就行了，这样一来，时间复杂度就是O(1)。

但是老三表示，怎么会老有人的名字老叫什么三、什么四的，起码得叫个"阿刚"、"小明"吧。

那么问题来了，阿刚、小明我们应该放在哪里呢？他们没法直接放到桶数组的对应下标位置。

所以，就引入了我们第二个关键要素哈希函数。

哈希函数

为了让映射能推广到所有情况，我们需要借助哈希函数 hashFunction映射到桶数组对应的位置。

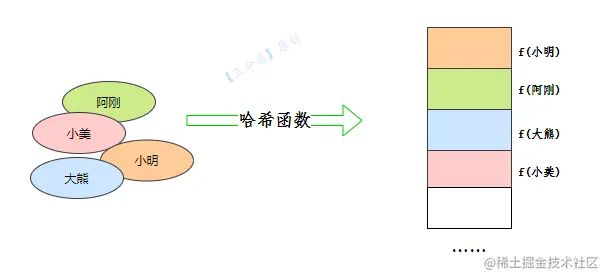
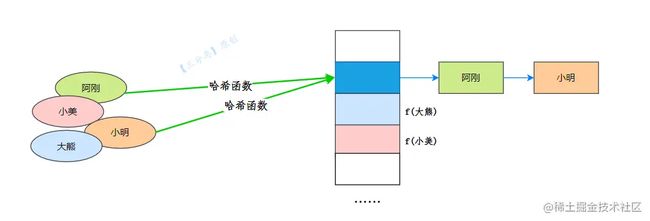
例如，我们上面说到的一些平平无奇的名字，阿刚、小明……我们要把它们映射到对应的桶中。

一般情况下，哈希函数通过对名字的HashCode进行运算，将名字映射到桶数组对应的索引。

哈希碰撞

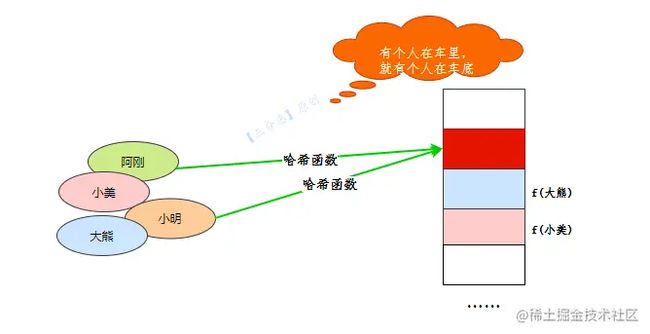
我们最理想的情况，就是通过哈希计算，各个元素找到空闲的坑位，但是现实往往不那么尽如人意，有时候，会发现，心上的城，已经长满了别人家的青藤。

阿刚和小明映射到了同一个位置，但这个位置只能容下一个人，这就叫哈希碰撞。

所以为了尽可能避免哈希碰撞呢，就需要精心设计哈希函数，我们希望哈希函数满足以下要求：

• 必须是一致的
• 计算简单
• 散列地址分布均匀

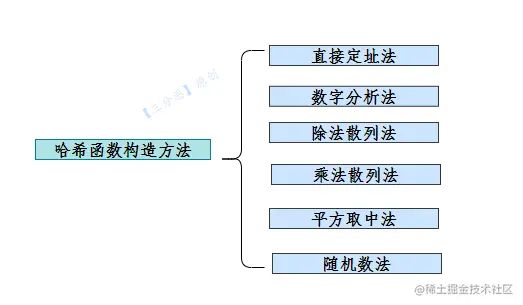
哈希函数构造方法

哈希函数的构造方法有很多，如下图，有些方法见名知义，篇幅所限，就不多讲。

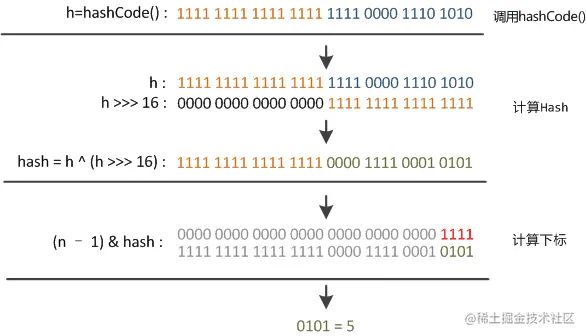
这里提一下HashMap的哈希函数：

    static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }
复制代码

整个过程大概如下：

• 利用hashCode()方法获取int类型的hashCode
• hashCode的高16位和hashCode的低16位做一个异或运算

hashCode右移16位，正好是32bit的一半。与自己本身做异或操作（相同为0，不同为1）。就是为了混合哈希值的高位和地位，增加低位的随机性。并且混合后的值也变相保持了高位的特征。

• 32位int型hashCode范围过大，需要与桶数组长度取模运算，得到索引值

int index = hash & (arrays.length-1);
复制代码

HashMap的哈希函数是非常优秀的设计，很值得学习。

处理哈希冲突的办法

即使再好的设计，也难免发生哈希碰撞。

那么，发生哈希碰撞，应该怎么处理呢？

拉链法

阿刚和小明在桶中发生了冲突，那我们在桶数组接一个小尾巴——用一个链表将他们俩存起来就可以了。

除了这个，还有啥办法呢？

唉，假如我们的桶数组还是有坑位，我们可以重新分配，这就是

线性探测法

使用线性探测法的前提是桶数组里面还有坑位。

常见的线性探测法有：

• 开放地址法

开放地址法就是一旦发生冲突，就去寻找下一个空的散列地址。

寻找下一个空的散列地址叫做探测，常见的探测方法有：线性探测法、二次探测法、随机探测法。

• 再哈希法

这个方法也很简单，利用不同的哈希函数再求得一个哈希地址，直到不出现冲突为止。

• 公共溢出区法

公共溢出区法就是再建一个公共溢出区，存储发生冲突的元素。

Java中的哈希结构

在Java的刷题中，我们有两种常用的哈希结构。

一种是HashMap，型的Hash结构。

一种是HashSet，没有重复元素的集合。

集合	底层实现	是否有序	数值是否可以重复	查询效率	增删效率
HashMap	数组/链表/红黑树	否	key不可重复，value可重复	O(1)	O(1)
HashSet	数组/链表/红黑树	否	不可重复	O(1)	O(1)

通常什么样的题目用Hash表呢？

还记得我们前面做过的求数字出现的次数吗？

判断一个元素是否出现过的场景，保底的我们应该立即想到哈希。

刷题现场

LeetCode1.两数之和 是比较典型的使用哈希表的例子，就不再来一遍了。

LeetCode242. 有效的字母异位词

☕ 题目：242. 有效的字母异位词

❓ 难度：简单

描述：

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

示例 1:

输入: s = "anagram", t = "nagaram"
输出: true
复制代码

示例 2:

输入: s = "rat", t = "car"
输出: false
复制代码

思路：

既然都说了要用哈希法，就懒得再写暴力法了。

我们可以用HashMap把字符出现的频率存储起来，s 出现一次频率+1，t 出现一次频率，判断最后hash所有位置value是否都为0。

思路很简单，代码实现如下：

    public boolean isAnagram(String s, String t) {
        if (s.length() != t.length()) {
            return false;
        }
        Map map = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            char sChar = s.charAt(i);
            char tChar = t.charAt(i);
            map.put(sChar, map.getOrDefault(sChar, 0) + 1);
            map.put(tChar, map.getOrDefault(tChar, 0) - 1);
        }
        for (Integer v : map.values()) {
            if (v != 0) {
                return false;
            }
        }
        return true;
    }
复制代码

还有另外一种实用数组作为哈希表的方法，据说可以加速，但是个人觉得用HashMap的方式比较好理解和记忆。

时间复杂度：O(n)

空间复杂度：O(n)

LeetCode1002. 查找常用字符

☕ 题目：1002. 查找常用字符

❓ 难度：简单

描述：

给定仅有小写字母组成的字符串数组 A，返回列表中的每个字符串中都显示的全部字符（包括重复字符）组成的列表。例如，如果一个字符在每个字符串中出现 3 次，但不是 4 次，则需要在最终答案中包含该字符 3 次。

你可以按任意顺序返回答案。

示例 1：

输入：["bella","label","roller"]
输出：["e","l","l"]
复制代码

示例 2：

输入：["cool","lock","cook"]
输出：["c","o"]
复制代码

LeetCode349. 两个数组的交集

☕ 题目：349. 两个数组的交集

❓ 难度：简单

描述：

给定两个数组，编写一个函数来计算它们的交集。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]
复制代码

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
复制代码

思路：

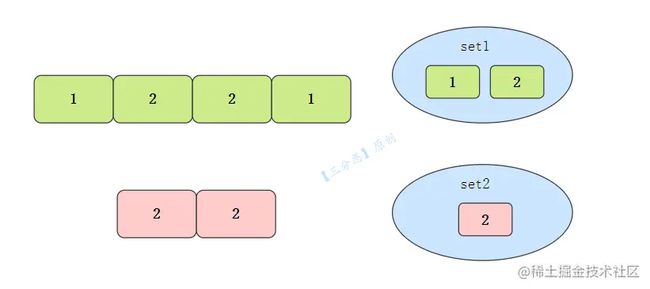
注意，求交集，是需要去重的。既然说到去重，我们自然想到了HashSet。

我们可以用两个HashSet，set1存储nums1元素，遍历nums2，判断元素是否存在于set1，用set2存储。

很好理解。

代码如下：

    public int[] intersection(int[] nums1, int[] nums2) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        if (len1 == 0 || len2 == 0) {
            return new int[0];
        }
        Set set1 = new HashSet<>();
        Set set2 = new HashSet<>();
        for (int i = 0; i < len1; i++) {
            set1.add(nums1[i]);
        }
        for (int j = 0; j < len2; j++) {
            if (set1.contains(nums2[j])) {
                set2.add(nums2[j]);
            }
        }
        int[] result = new int[set1.size()];
        int k = 0;
        for (int value : set2) {
            result[k++] = value;
        }
        return result;
    }
复制代码

时间复杂度：O(n)

空间复杂度：O(n)

LeetCode454. 四数相加 II

☕ 题目：454. 四数相加 II 

❓ 难度：中等

描述：

给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ，使得 A[i] + B[j] + C[k] + D[l] = 0。

为了使问题简单化，所有的 A, B, C, D 具有相同的长度 N，且 0 ≤ N ≤ 500 。所有整数的范围在 -228 到 228 - 1 之间，最终结果不会超过 231 - 1 。

例如:

输入:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]

输出:
2

解释:
两个元组如下:
1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0

复制代码

思路：

我们的思路是四个数组分两组，一组存HashMap，另一组和HashMap比较。

• 首先定义 一个HashMap，key放A和B两数之和，value 放A和B两数之和出现的次数。
• 遍历大A和大B数组，统计两个数组元素之和，和出现的次数，放到map中。
• 定义int变量count，用来统计a+b+c+d = 0 出现的次数。
• 在遍历大C和大D数组，找到如果 0-(C+D) 在map中出现过的话，就用res把map中key出现的次数
• 最后返回统计值 count

    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        Map map = new HashMap<>();
        int res = 0;
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                int sumAB = nums1[i] + nums2[j];
                map.put(sumAB, map.getOrDefault(sumAB, 0) + 1);
            }
        }

        for (int i = 0; i < nums3.length; i++) {
            for (int j = 0; j < nums4.length; j++) {
                int sumCD = -(nums3[i] + nums4[j]);
                if (map.containsKey(sumCD)) {
                    res+=map.get(sumCD);
                }
            }
        }
        return res;
    }
复制代码

时间复杂度：O(n²)

空间复杂度：O(n)

LeetCode383. 赎金信

☕ 题目：454. 四数相加 II

❓ 难度：简单

描述：

给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串，判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成，返回 true ；否则返回 false。

(题目说明：为了不暴露赎金信字迹，要从杂志上搜索各个需要的字母，组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)

示例 1：

输入：ransomNote = "a", magazine = "b"
输出：false
复制代码

示例 2：

输入：ransomNote = "aa", magazine = "ab"
输出：false
复制代码

示例 3：

输入：ransomNote = "aa", magazine = "aab"
输出：true
复制代码

思路

这个题解法也很好像。

用HashMap存储报刊数组字符以及字符出现的次数，遍历赎金信数组，取对应的字符。

注意，这里每个字符只能使用一次，所以取字符的时候需要减1。

代码如下：

    public boolean canConstruct(String ransomNote, String magazine) {
        Map hash = new HashMap<>();
        for (int i = 0; i < magazine.length(); i++) {
            char m = magazine.charAt(i);
            hash.put(m, hash.getOrDefault(m, 0) + 1);
        }
        for (int i = 0; i < ransomNote.length(); i++) {
            char r = ransomNote.charAt(i);
            if (!hash.containsKey(r)) {
                return false;
            }
            if (hash.get(r) == 0) {
                return false;
            }
            hash.put(r, hash.get(r) - 1);
        }
        return true;
    }
复制代码

时间复杂度：O(n)

空间复杂度：O(n)

LeetCode202. 快乐数

☕ 题目：202. 快乐数 

❓ 难度：简单

描述：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果 可以变为 1，那么这个数就是快乐数。

如果 n 是快乐数就返回 true ；不是，则返回 false 。

示例 1：

输入：19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
复制代码

示例 2：

输入：n = 2
输出：false
复制代码

思路：

这道题解题的关键在于也可能是 无限循环 但始终变不到 1。。

咱们肯定不能让它取快乐数这个过程无限循环下去，但是它既然循环了，那么各位数的平方和肯定会重复，这就成了判断元素是否出现的问题。

这道题我们可以用HashSet存储平方和，如果当前平方和已经出现过，说明已经开始无限循环。

    public boolean isHappy(int n) {
    Set set = new HashSet<>();
    while (true) {
        int sum = getSum(n);
        //开心数
        if (sum == 1) {
            return true;
        }
        //sum出现过
        if (set.contains(sum)) {
            return false;
        } else {
            set.add(sum);
        }
        n = sum;
    }
}

    /**
     * @return int
     * @Description: 获取平方和
     * @date 2021/8/11 22:41
     */
    int getSum(int n) {
        int sum = 0;
        while (n > 0) {
            int temp = n % 10;
            sum += temp * temp;
            n = n / 10;
        }
        return sum;
    }
复制代码

时间复杂度：O(logn)

空间复杂度：O(logn)

这道题还可以用双指针的方式，用两个数，一个快指针，一个慢指针，如果进入循环，最终两个指针会相遇。

总结

还是一个顺口溜：

简单的事情重复做，重复的事情认真做，认真的事情有创造性地做！

为了帮助大家提高自己的算法能力，为大家搜罗整理到了几份非常nice的算法笔记，限于平台原因，只能展示部分截图，有需要的小伙伴 工众号【不脱发有志青年】免费获取

第一份

这份笔记内容全部都是纯手打，排序算法/数据结构的代码可能不是最优解，代码的实现都是以比较容易理解的方式去写的。几乎每句代码都有对应的注释，应该是能看懂的。

目录概览