Matplotlib 数据可视化(读书笔记)
Python 数据科学手册第四章读书笔记,仅供学习交流使用
4. Matplotlib 数据可视化
4.1 Matplotlib 常用技巧
4.1.1 导入 Matplotlib
plt 是最常用的接口:
import matplotlib as mpl
import matplotlib.pyplot as plt
4.1.2 设置绘图样式
我们将使用 plt.style 来选择图形的绘图风格,现在选择经典(classic)风格,这样画出来的图都是经典的 Matplotlib 风格了:
plt.style.use('classic')
4.1.3 用不用 show()? 如何显示图形
-
在脚本中画图
如果在脚本中使用 Matplotlib,那么显示图形必须使用 plt.show()。plt.show() 会启动一个事件循环(event loop),并找到当前可用的图形对象,然后打开一个或多个交互式窗口显示图形。
例如,你现在有一个名为 myplot.py 的文件:
# file: myplot.py import matplotlib.pyplot as plt import numpy as np x = np.linspace(0, 10, 100) # 创建一个100个元素的数组,这5个数均匀地分配到0~10 plt.plot(x, np.sin(x)) plt.plot(x, np.cos(x)) plt.show()你可以在命令行工具中执行这个脚本:
$ python myplot.py一个 Python 会话中只能使用一次 plt.show(),因此通常把它放在脚本最后, 多个 plt.show() 会导致难以预料的显示异常,应该尽量避免。
-
在 IPython shell 中画图
为了启用这个模式,你需要在启动 ipython 后使用 %matplotlib 魔法命令:
%matplotlib Using matplotlib backend: <object object at 0x0000021188C9CB40>import matplotlib.pyplot as plt此后的任何 plt 命令都会自动打开一个图形窗口,增加新的命令,图形就会更新。有一些变化(例如改变已经画好的线条属性)不会自动及时更新;对于这些变化,可以使用 plt.draw() 强制更新。在 IPython shell 中启动 Matplotlib 模式之后,就不需要使用 plt.show() 了。
-
在 IPython Notebook 中画图
用 IPython Notebook 进行交互式画图与使用 IPython shell 类似,也需要 %matplotlib 命令。你可以将图形直接嵌在 IPython Notebook 页面中,有两种展现形式。
- %matplotlib nootbook 会在 Noyebook 中启动交互式图形。
- %matplotlib inline 会在 Notebook 中启动静态图形。
本书统一使用 %matplotlib inline:
%matplotlib inline运行命令之后(每一个 Notebook 核心任务/会话只需要运行一次),在每一个Notebook 的单元中创建图形就会直接将 PNG 格式图形文件嵌入在单元中:
import numpy as np x = np.linspace(0, 10, 100) # 创建一个100个元素的数组,这5个数均匀地分配到0~10 fig = plt.figure() plt.plot(x, np.sin(x), '-') plt.plot(x, np.cos(x), '--');
4.1.4 将图形保存为文件
Matplotlib 的一个优点是能够将图形保存为各种不同的数据格式。你可以用 savefig() 命令将图形保存为文件。例如,如果要将图形保存为 PNG 格式,你可以运用这行代码:
fig.savefig('my_figure.png')
这样工作文件夹中就有了一个 my_figure.png 文件:
!ls -lh my_figure.png
为了确定文件中是否有我们需要的内容,可以用 IPython 的 Image 对象来显示文件内容:
from IPython.display import Image
Image('my_figure.png')
在 savefig() 里面,保存的文件格式就是文件的扩展名。Matplotlib 支持许多图形格式,具体格式由操作系统已安装的图形显示接口决定。你可以通过 canvas 对象的方法查看系统支持的文件格式:
fig.canvas.get_supported_filetypes()
{'eps': 'Encapsulated Postscript',
'jpg': 'Joint Photographic Experts Group',
'jpeg': 'Joint Photographic Experts Group',
'pdf': 'Portable Document Format',
'pgf': 'PGF code for LaTeX',
'png': 'Portable Network Graphics',
'ps': 'Postscript',
'raw': 'Raw RGBA bitmap',
'rgba': 'Raw RGBA bitmap',
'svg': 'Scalable Vector Graphics',
'svgz': 'Scalable Vector Graphics',
'tif': 'Tagged Image File Format',
'tiff': 'Tagged Image File Format'}
需要注意的是,当你保存图形文件时,不需要使用 plt.show() 或者前面介绍过的命令。
4.2 两种画图接口
4.2.1 MATLAB 风格接口
MATLAB 风格的工具位于 pyplot(plt)接口中。
plt.figure() # 创建图形
# 创建两个子图中的第一个,设置坐标轴
plt.subplot(2, 1, 1) # (行、列、子图编号)
# 创建两个子图中的第二个,设置坐标轴
plt.subplot(2, 1, 2)
plt.plot(x, np.cos(x));
这种接口最重要的特性就是有状态的:它会持续跟踪“当前的”图形和坐标轴,所有 plt 命令都可以应用。你可以用 plt.gcf()(获取当前图形) 和 plt.gca() (获取当前坐标轴) 来查看具体信息。
4.2.2 面向对象接口
用面向对象接口重新创建之前的图形:
# 先创建图形网格
# ax 是一个包含两个 Axes 对象的数组
fig, ax = plt.subplots(2)
# 在每个对象上调用 plot() 方法
ax[0].plot(x, np.sin(x))
ax[1].plot(x, np.cos(x));
4.3 简易线形图
在 Notebook 中画图,需要导入以下命令:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
要画 Matplotlib 图形时,需要先创建一个图形 fig 和一个坐标轴 ax。创建图形和坐标轴最简单的做法:
fig = plt.figure()
ax = plt.axes()
在 Matplotlib 里面,figure(plt.Figure 类的一个实例)可以被看成是一个能够容纳各种坐标轴、图形、文字和标签的容器。就像你在图中看见的那样,axes(plt.Axes 类的一个实例)是一个带有刻度和标签的矩形,最终会包含所有可视化的图形元素。
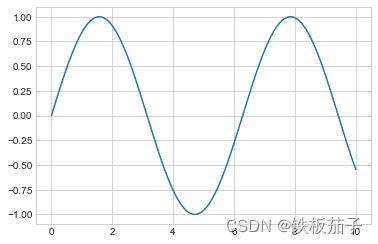
创建好坐标轴之后,就可以用 ax.plot 画图了。从一组简单的正弦函数开始:
fig = plt.figure()
ax = plt.axes()
x = np.linspace(0, 10, 1000)
ax.plot(x, np.sin(x));
另外,也可以用 pylab 接口画图,这时图形和坐标轴都在底层执行:
plt.plot(x, np.sin(x));
plt.plot(x, np.sin(x))
plt.plot(x, np.cos(x));
4.3.1 调整图形:线条的颜色与风格
要修改颜色,就可以使用 color 参数:
plt.plot(x, np.sin(x - 0), color='blue') # 标准颜色名称
plt.plot(x, np.sin(x - 1), color='g') # 缩写颜色代码(rgbcmyk)
plt.plot(x, np.sin(x - 2), color='0.75') # 范围在0~1的灰度值
plt.plot(x, np.sin(x - 3), color='#FFDD44') # 十六进制(RRGGBB, 00~FF)
plt.plot(x, np.sin(x - 4), color=(1.0, 0.2, 0.3)) # RGB 元组,范围在0~1
plt.plot(x, np.sin(x - 5), color='chartreuse'); # HTML 颜色名称
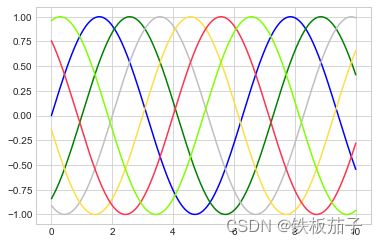
如果不指定颜色,Matplotlib 就会为多条线自动循环使用一组默认的颜色。
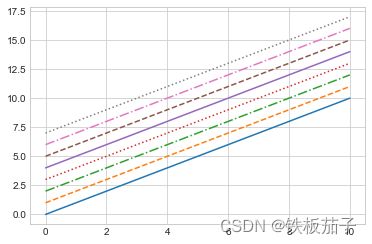
可以用 linestyle 调整线条的风格:
plt.plot(x, x + 0, linestyle='solid')
plt.plot(x, x + 1, linestyle='dashed')
plt.plot(x, x + 2, linestyle='dashdot')
plt.plot(x, x + 3, linestyle='dotted');
简写:
plt.plot(x, x + 4, linestyle='-') # 实线
plt.plot(x, x + 5, linestyle='--') # 虚线
plt.plot(x, x + 6, linestyle='-.') # 点划线
plt.plot(x, x + 7, linestyle=':'); # 实点线
可以把 linestyle 和 color 编码结合起来,作为 plt.plot() 函数的一个非关键字参数使用:
plt.plot(x, x + 0, '-g') # 绿色实线
plt.plot(x, x + 1, '--c') # 青色虚线
plt.plot(x, x + 2, '-.k') # 黑色点划线
plt.plot(x, x + 3, ':r'); # 红色实点线
4.3.2 调整图形:坐标轴上下限
调整坐标轴上下限最基础的方法是 plt.xlim() 和 plt.ylim():
plt.plot(x, np.sin(x))
plt.xlim(-1, 11)
plt.ylim(-1.5, 1.5);
plt.plot(x, np.sin(x))
plt.xlim(10, 0)
plt.ylim(1.2, -1.2);
还有一个方法是 plt.axis() ,通过传入[xmin, xmax, ymin, ymax]对应的值,plt.axis() 方法可以让你用一行代码设置x和y的限值:
plt.plot(x, np.sin(x))
plt.axis([-1, 11, -1.5, 1.5]);
它还可以按照图形的内容自动收紧坐标轴,不留空白区域:
plt.plot(x, np.sin(x))
plt.axis('tight');
还可以实现更高级的配置,例如让屏幕上显示的图形分辨率为1:1,x 轴单位长度与 y 轴单位长度相等:
plt.plot(x, np.sin(x))
plt.axis('equal');
4.3.3 设置图形标签
图形标题与坐标轴标题是最简单的标签:
plt.plot(x, np.sin(x))
plt.title("A Sine Curve")
plt.xlabel("x")
plt.ylabel("sin(x)");

在单个坐标轴上显示多条线时,创建图例显示每条线是很有效的方法。plt.legend() 是一个简单快速创建图例的方法。虽然有不少设置图例的方法,但在 plt.plot 函数中用 label 参数为每条线设置一个标签最简单:
plt.plot(x, np.sin(x), '-g', label='sin(x)')
plt.plot(x, np.cos(x), ':b', label='cos(x)')
plt.axis('equal')
plt.legend(); # 显示多例图例
4.4 简易散点图
开始时同样需要在 Notebook 中导入函数:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
4.4.1 用 plt.plot 画散点图
x = np.linspace(0, 10, 30)
y = np.sin(x)
plt.plot(x, y, 'o', color='black');

函数的第三个参数是一个字符,表示图形符号的类型,与之前的 ‘-’ 和 ‘–’ 设置线条属性类似。
rng = np.random.RandomState(0)
for marker in ['o', '.', ',', 'x', '+', 'v', '^', '<', '>', 's', 'd']:
plt.plot(rng.rand(5), rng.rand(5), marker,
label="marker='{0}".format(marker))
plt.legend(numpoints=1)
plt.xlim(0, 1.8)
这些代码还可以与线条、颜色代码组合起来,画出一条连续散点的线:
plt.plot(x, y, '-ok'); # 直线(-)、圆圈(o)、黑色(k)
plt.plot(x, y, '-p', color='gray',
markersize=15, linewidth=4, # linewidth 设置线条粗细
markerfacecolor='white',
markeredgecolor='gray',
markeredgewidth=2)
plt.ylim(-1.2, 1.2);
4.4.2 用 plt.scatter 画散点图
plt.scatter(x, y, marker='o');
plt.scatter 与 plt.plot 的主要差别在于,前者在创建散点图时具有更高的灵活性,可以单独控制每个散点与数据匹配,也可以让每个散点具有不同的属性(大小,表面颜色、边框颜色等)。
创建有各个颜色和大小的散点,用 alpha 参数调整透明度:
rng = np.random.RandomState(0)
x = rng.randn(100)
y = rng.randn(100)
colors = rng.rand(100)
sizes = 100 * rng.rand(100)
plt.scatter(x, y, c=colors, s=sizes, alpha=0.3,
cmap='viridis')
plt.colorbar(); # 显示颜色条
请注意,颜色自动映射为颜色条,散点的大小以像素为单位。这样,散点的颜色与大小就可以在可视化图中显示多维的信息了。
例如,可以用 Scikit-Learn 程序库里的鸢尾花(iris)数据来演示。它里面有三种鸢尾花,每个样本是一种花,其花瓣(petal)与花萼的长度与宽度都经过仔细测量:
from sklearn.datasets import load_iris
iris = load_iris()
features = iris.data.T
plt.scatter(features[0], features[1], alpha=0.2,
s=100*features[3], c=iris.target, cmap='viridis')
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1]);
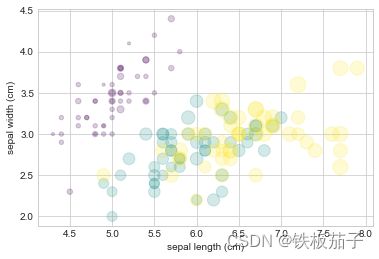
散点图可以让我们同时看见不同维度的数据:每个点的坐标值(x, y) 分别表示花萼的长度和宽度,而点的大小表示花瓣的宽度,三种颜色对应三种不同颜色的鸢尾花。这类多颜色与多特征的散点图在探索与演示数据时非常有用。
数据达到几千个散点时,plt.plot 的效率大大高于 plt.scatter.
4.5 可视化异常处理
4.5.1 基本误差线
基本误差线可以通过一个 Matplotlib 函数来创建:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
x = np.linspace(0, 10, 50)
dy = 0.8
y = np.sin(x) + dy * np.random.randn(50)
plt.errorbar(x, y, yerr=dy, fmt='.k');
其中,fmt 是一种控制线条和点的外观的代码格式,语法与 plt.plot 的缩写代码相同。
errorbar方法的一些参数说明:
- yerr: 绘制垂直方向的误差线
- xerr:绘制水平方向的误差线
- fmt: 线条格式
- ecolor: 误差线的颜色
- elinewidth:误差线的宽度
- capsize: 误差线的长度
- one-sided 单侧误差线
除了基本选项之外,errorbar 还有许多改善结果的选项,通过这些额外的选项,你可以轻松定义误差线图形的绘图风格,让误差线的颜色比数据点的颜色浅一点会更好,尤其是那些比较密集的图形:
plt.errorbar(x, y, yerr=dy, fmt='o', color='black',
ecolor='lightgray', elinewidth=3, capsize=0);
4.5.2 连续误差
我们将用 Scikit-Learn 程序库 API 里面一个简单的高斯过程回归方法来演示。这是一种用非常灵活的非参数方程对带有不确定性的连续测量值进行拟合的方法。
from sklearn.gaussian_process import GaussianProcessRegressor
# 定义模型和画图的数据
model = lambda x: x * np.sin(x)
xdata = np.array([1, 3, 5, 6, 8])
ydata = model(xdata)
# 计算高斯过程拟合结果
gp = GaussianProcessRegressor()
gp.fit(xdata[:, np.newaxis], ydata)
xfit = np.linspace(0, 10, 1000)
yfit, y_std = gp.predict(xfit[:, np.newaxis], return_std=True)
dyfit = 2 * np.sqrt(y_std) # 2*sigma~95%置信区间
# 将结果可视化
plt.plot(xdata, ydata, 'or')
plt.plot(xfit, yfit, '-', color='gray')
plt.fill_between(xfit, yfit - dyfit, yfit + dyfit,
color='gray', alpha=0.2)
plt.xlim(0, 10);
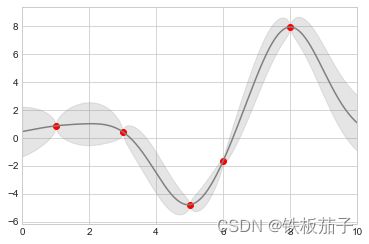
我们将 fil_between 函数设置为:首先传入 x 轴坐标值,然后传入 y 轴下边界以及 y 轴上边界,这样整个区域就被误差线填充了。
4.6 密度线与等高线图
有时候在二维图上用等高线图或彩色图来表示三维数据是一个不错的方法。Matplotlib 提供了三个函数来解决这个问题:用 plt.contour 画等高线图、用 plt.contourf 画带有填充色的等高线图的色彩、用 plt.imshow 显示图形。
首先打开一个 Notebook,然后导入画图需要的函数:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
import numpy as np
三维函数的可视化
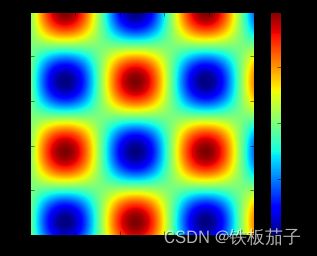
首先用 z = f(x, y),演示一个等高线图,按照下面的方式生成函数 f 样本数据:
def f(x, y):
return np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)
等高线图可以用 plt.contour 来创建。它需要三个参数: x 轴、y 轴和 z 轴三个坐标轴的网格数据,x 轴和 y 轴表示图形中的位置,而 z 轴通过等高线的等级来表示。用 np.meshgrid 函数来准备这些数据可能是最简单的方法,它可以从一维数组构建二维网格数据:
x = np.linspace(0, 5, 50)
y = np.linspace(0, 5, 40)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
来看看标准的线形等高线图:
plt.contour(X, Y, Z, colors='black');

需要注意的是:当图形只有一种颜色时,默认使用虚线表示负数,使用实线表示正数。另外,可以使用 cmap 参数设置一个线条配色方案来自定义颜色。还可以让更多的线条显示不同的颜色——可以将数据范围等分为20份,然后用不同的颜色表示:
plt.contour(X, Y, Z, 20, cmap='RdGy');
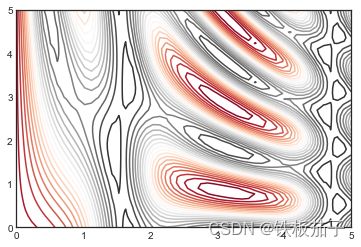
现在使用 RdGy(红-灰,Red-Gray 的缩写)配色方案,这对于数据集中度的显示效果比较好。Matplotlib 有非常丰富的配色方案,可以在 IPython 中用 Tab 键浏览 plt.cm.模块对应的信息:
虽然这幅图看起来漂亮很多,但线条之间的间隙有点大。我们可以通过 plt.contourf() 函数来填充等高线图,它的语法和 plt.contour() 一样的。
另外还可以通过 plt.colorbar() 命令自动创建一个表示图形各种颜色对应标签信息的颜色条:
plt.contourf(X, Y, Z, 20, cmap='RdGy')
plt.colorbar();
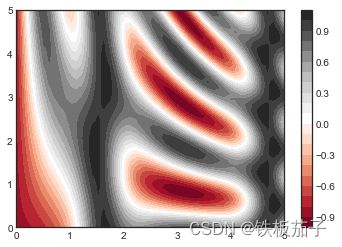
通过颜色条可以清晰看出:黑色区域是“波峰”,红色区域是“波谷”。
但是图形不是那么干净,这是由于颜色的改变是一个离散而非连续的过程,这并不是我们想要的效果。可以通过 plt.imshow() 函数来处理,它可以将二维数组渲染成渐变图:
plt.imshow(Z, extent=[0, 5, 0, 5], origin='lower',
cmap='RdGy')
plt.colorbar()
plt.axis(aspect='image');
- plt.imshow() 不支持用 x 轴和 y 轴设置网格,而是必须通过 extent 参数设置图形的坐标范围 [xmin, xmax, ymin, ymax]。
- plt.imshow() 默认使用标准的图形数组定义,就是原点位于左上角(浏览器都是如此),而不是绝大多数等高线图中使用的左下角,这一点在显示网格数据图形的时候必须调整。
- plt.imshow() 会自动调整坐标轴的精度以适应数据显示。你可以通过 plt.axis(aspect=‘image’) 来设置 x 轴和 y 轴的单位。
最后还有一个可能用到的方法,就是将等高线与彩色图结合起来,例如,用一幅背景色半透明的彩色图(可以通过 alpha 参数设置透明度),与另一幅坐标轴相同、带数据标签的等高线图叠放在一起(用 plt.clabel() 函数实现):
contours = plt.contour(X, Y, Z, 2, colors='black')
plt.clabel(contours, inline=True, fontsize=8)
plt.imshow(Z, extent=[0, 5, 0, 5], origin='lower',
cmap='RdGy', alpha=0.5)
plt.colorbar();
4.7 频次直方图、数据区间划分和分布密度
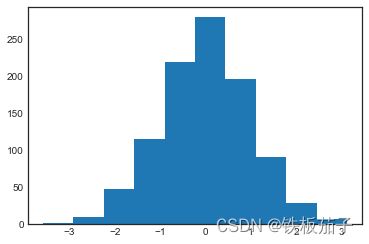
一个简易的频次直方图可以是理解数据集的良好开端。只要导入画图的函数,只用一行代码就可以创建一个简易的频次直方图:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
data = np.random.randn(1000)
plt.hist(data);
hist() 有许多用来调整计算过程和显示效果的选项,下面是一个更加个性化的频次直方图:
plt.hist(data, bins=30, density=True, alpha=0.5,
histtype='stepfilled', color='steelblue',
edgecolor='none');
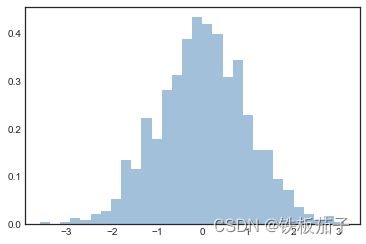
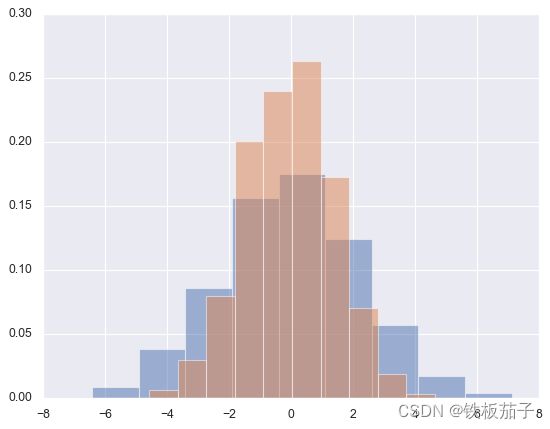
在用频次直方图对不同分布特征的样本进行对比时,将 histtype=‘stepfilled’ 与透明性设置参数 alpha 搭配使用的效果非常好:
x1 = np.random.normal(0, 0.8, 1000)
x2 = np.random.normal(-2, 1, 1000)
x3 = np.random.normal(3, 2, 1000)
kwargs = dict( histtype='stepfilled', alpha=0.3, density=True, bins=40)
plt.hist(x1, **kwargs)
plt.hist(x2, **kwargs)
plt.hist(x3, **kwargs);
如果你只需要计算频次直方图(就是计算每段区间的样本数),而并不想画图显示它们,那么可以直接用 np.histogram():
# 如果bins是个数字,那么它设置的是bin的个数,也就是沿着x轴划分多少个独立的绘图区域。
counts, bin_edges = np.histogram(data, bins=5)
print(counts)
[ 12 164 500 288 36]
二维频次直方图与数据区间划分
就像将一维数组分为区间创建一维频次直方图一样,我们也可以将二维数组按照二维区间进行切分,来创建二维频次直方图。下面将简单介绍几种创建二维频次直方图的方法。首先,用一个多元高斯分布生成 x 轴和 y 轴的样本数据:
mean = [0, 0]
# 分布的协方差矩阵,它的形状必须是(n,n),也就是必须是一个行数和列数相等的类似正方形矩阵,它必须是对称的和正半定的,才能进行适当的采样。
cov = [[1, 1], [1, 2]]
x, y = np.random.multivariate_normal(mean, cov, 10000).T
-
plt.hist2d:二维频次直方图
画二维频次直方图最简单的方法就是使用 Matplotlib 的 plt.hist2d 函数:
plt.hist2d(x, y, bins=30, cmap='Blues') cb = plt.colorbar() cb.set_label('counts in bin')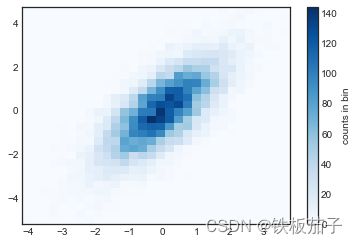
与 plt.hist 函数一样,plt.hist2d 也有许多调整图形与区间划分的配置选项,详细内容都在程序文档中。另外,就像 plt.hist 有一个只计算结果不画图的 np.histogram 函数一样,plt.his2d 也有的类似函数是 np.histogram2d,其用法如下所示:counts, xedges, yedges = np.histogram2d(x, y, bins=30) -
plt.hexbin:六边形区间划分
二维频次直方图是由与坐标轴正交的方块分割而成的,还有一种常用方式就是用正六边形分割。Matplotlib 提供了 plt.hexbin 满足此类要求,将二维数据集分割成蜂窝状:
plt.hexbin(x, y, gridsize=30, cmap='Blues') cb = plt.colorbar(label='count in bin')
plt.hexbin 同样也有一大堆有趣的配置选项,包括为每个数据点设置不同的权重,以及用任意的 NumPy 累计函数改变每个六边形区间划分的结果(权重均值、标准差等指标)。 -
核密度估计
还有一种评估多维数据分布密度的常用方法就是核密度估计。现在来简单的演示如何用 KDE 方法“抹掉”空间中离散的数据点,从而拟合出一个平滑的函数。在 scipy.stats 程序包里面有一个简单快速的 KDE 实现方法:
from scipy.stats import gaussian_kde #拟合数组维度[Ndim, Nsamples] data = np.vstack([x, y]) # 按垂直方向(行顺序)堆叠数组构成一个新的数组 kde = gaussian_kde(data) # 用一对规则的网格数据进行拟合 xgrid = np.linspace(-3.5, 3.5, 40) ygrid = np.linspace(-6, 6, 40) Xgrid, Ygrid = np.meshgrid(xgrid, ygrid) # 生成网格点坐标矩阵 Z = kde.evaluate(np.vstack([Xgrid.ravel(), Ygrid.ravel()])) # ravel()方法将数组维度拉成一维数组 # 画出结果图 plt.imshow(Z.reshape(Xgrid.shape), origin='lower', aspect='auto', extent=[-3.5, 3.5, -6, 6], cmap = 'Blues') cb = plt.colorbar() cb.set_label("density")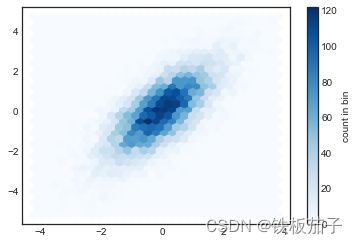
KDE 方法通过不同的平滑带宽长度在拟合函数的准确性与平滑性之间作出权衡。想找到恰当的平滑带宽长度是件很困难的事,gaussian_kde 通过一种经验方法试图找到输入数据平滑长度的近似最优解。
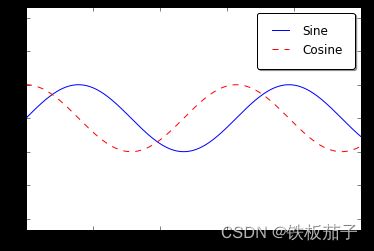
4.8 配置图例
现在将介绍如何在 Matplotlib 中自定义图例的位置与艺术风格:
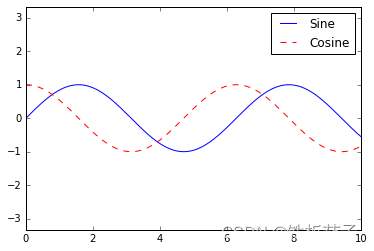
可以用 plt.legend() 命令来创建最简单的图例,它会自动创建一个包含每个图形元素的图例:
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
import numpy as np
x = np.linspace(0, 10, 1000)
fig, ax = plt.subplots()
ax.plot(x, np.sin(x), '-b', label='Sine')
ax.plot(x, np.cos(x), '--r', label='Cosine')
ax.axis('equal') # x 轴和 y 轴轴间距相等
leg = ax.legend();
```
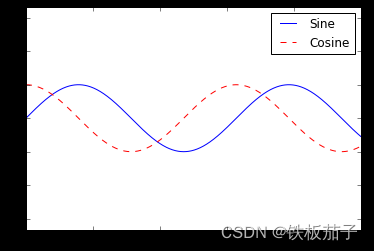
但是,我们需要经常对图例进行各种个性化配置。例如,我们想设置图例的位置,并取消外边框:
```python
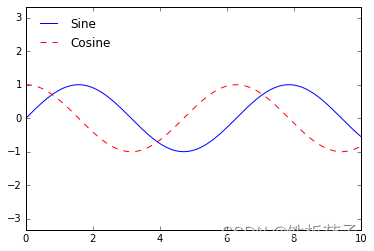
ax.legend(loc='upper left', frameon=False)
fig
ax.legend(frameon=False, loc='lower center', ncol=2)
fig
```
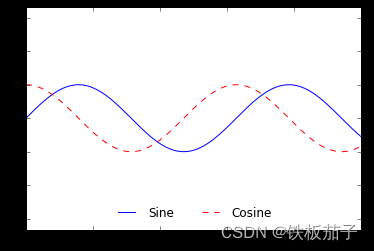
还可以为图例定义圆角边框(fancybox)、增加阴影、改变外边框透明度(framealpha 值),或者改变文字间距:
```python
ax.legend(fancybox=True, framealpha=1, shadow=True, borderpad=1)
fig
4.8.1 选择图例显示的元素
图例会默认显示所有元素的标签。如果不想显示全部,可以用一些图例命令来指定显示图例中哪些元素和标签。plt.plot() 命令可以一次创建多条线,返回线条实例列表。一种方法是将需要显示的线条传入plt.legend(),另一种方法是只需要在图例中显示的线条设置标签:
y = np.sin(x[:, np.newaxis] + np.pi * np.arange(0, 2, 0.5))
lines = plt.plot(x, y)
# lines 变量是一组 plt.Line2D 实例
plt.legend(lines[:2], ['first', 'second']);

在实践中,我们发现第一种方法更清晰。当然也可以只为需要在图例中显示的元素设置标签:
plt.plot(x, y[:, 0], label='first')
plt.plot(x, y[:, 1], label='second')
plt.plot(x, y[:, 2:])
plt.legend(framealpha=1, frameon=True);
需要注意的是,默认情况下图例会自动忽略那些不带标签的元素。
4.8.2 在图例中显示不同尺寸的点
有时,默认的图例仍不能满足我们的可视化需求。例如,你可能需要用不同尺寸的点来表示数据的特征,并且希望创建这样的图例来反映这些特征。下面的示例将用点的尺寸来表明美国加州不同城市的人口数量。如果我们想要一个通过不同尺寸的点显示不同人口数量级的图例,可以通过隐藏一些数据标签来实现这个效果:
import pandas as pd
cities = pd.read_csv('data/california_cities.csv')
# 提取感兴趣的数据
lat, lon = cities['latd'], cities['longd']
population, area = cities['population_total'], cities['area_total_km2']
# 用不同尺寸和颜色的散点图表示数据,但是不带标签
plt.scatter(lon, lat, label=None,
c=np.log10(population), cmap='viridis',
s=area, linewidth=0, alpha=0.5)
plt.axis('equal')
plt.xlabel('longitude')
plt.ylabel('latitude')
plt.colorbar(label='log$_{10}$(population)')
plt.clim(3, 7)
# 下面创建一个图例
# 画一些带标签和尺寸的空列表
for area in [100, 300, 500]:
plt.scatter([], [], c='k', alpha=0.3, s=area,
label=str(area) + ' km$^2$')
plt.legend(scatterpoints=1, frameon=False, labelspacing=1, title='City Area')
plt.title('California Cities: Area and Population');
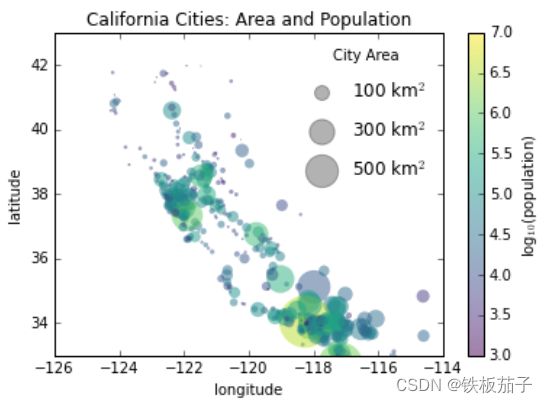
由于图例通常是图形中对象的参照,因此我们如果想要显示某种形状,就需要将它画出来。但是在这个图例中,我们想要的(灰色圆圈)并不在图形中,因此把它们用空列表假装画出来。还需要注意的是,图例只会显示带标签的元素。
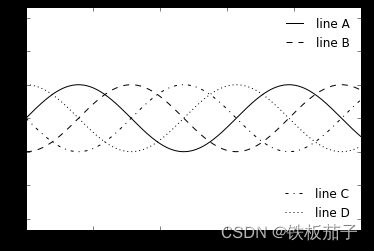
4.8.3 同时显示多个图例
有时,我们可能需要在同一张图上显示多个图例,不过,用 Matplotlib 解决这个问题并不容易,因为通过标准的 legend() 方法创建第二个图例,那么第一个图例会被覆盖。但是, 我们可以通过从头开始创建一个新的图例艺术家对象,然后用底层的 ax.add_artist() 方法在图上添加第二个图例:
fig, ax = plt.subplots()
lines = []
styles = ['-', '--', '-.', ':']
x = np.linspace(0, 10, 1000)
for i in range(4):
lines += ax.plot(x, np.sin(x - i * np.pi / 2),
styles[i], color='black')
ax.axis('equal')
# 设置第一个图例要显示的线条和标签
ax.legend(lines[:2], ['line A', 'line B'],
loc='upper right', frameon=False)
# 创建第二个图例,过 add_artist 方法添加到图上
from matplotlib.legend import Legend
leg = Legend(ax, lines[2:], ['line C', 'line D'],
loc='lower right', frameon=False)
ax.add_artist(leg);
4.9 配置颜色条
在 Matplotlib 里面,颜色条是一个独立的坐标轴,可以指明图形中颜色的含义。
首先导入需要使用的画图工具:
import matplotlib.pyplot as plt
plt.style.use('classic')
%matplotlib inline
import numpy as np
通过 plt.colorbar函数就可以创建最简单的颜色条:
x = np.linspace(0, 10, 1000)
I = np.sin(x) * np.cos(x[:, np.newaxis])
plt.imshow(I)
plt.colorbar();
4.9.1 配置颜色条
可以通过 cmap参数为图形配置颜色条的配色方案:
plt.imshow(I, cmap='gray');

所有可用的配色方案在 plt.cm命名空间里面,在 IPython 里通过 Tab 键就可以查看所有的配色方案:
plt.cm.<Tab>
有了这么多能够作为备选的配色方案只是第一步,更重要的是如何确定使用哪种方案。最终的选择结果可能和你一开始想用的有很大不同。
-
选择配色方案
一般情况下只需要关注三种不同的配色方案:
- 顺序配色方案:由一组连续的颜色构成的配色方案(例如 binary 或 viridis)。
- 互逆配色方案:通常由两组互补的颜色构成,表示正反两种含义(例如 RdBu 或 PuOr)。
- 定性配色方案:随机顺序的一组颜色(例如 rainbow 或 jet)。
jet 是一种定性配色方案,曾是 Matplotlib 2.0 之前所有版本的默认配色方案。随着图形亮度的提升,经常会出现颜色无法区分的问题。
可以通过把 jet 转换为黑白的灰度图看看具体的颜色:
from matplotlib.colors import LinearSegmentedColormap def grayscale_cmap(cmap): """为配色方案显示灰度""" cmap = plt.cm.get_cmap(cmap) colors = cmap(np.arange(cmap.N)) # 将RGBA色转化为不同亮度的灰度值 # 参考连接 http://alienryderflex.com/hsp.html RGB_weight = [0.299, 0.587, 0.114] luminance = np.sqrt(np.dot(colors[:, :3] ** 2, RGB_weight)) # np.dot矩阵乘法 colors[:, :3] = luminance[:, np.newaxis] return LinearSegmentedColormap.from_list(cmap.name + "_gray", colors, cmap.N) def view_colormap(cmap): """用等价的灰度图表示配色方案""" cmap = plt.cm.get_cmap(cmap) colors = cmap(np.arange(cmap.N)) cmap = grayscale_cmap(cmap) grayscale = cmap(np.arange(cmap.N)) fig, ax = plt.subplots(2, figsize=(6, 2), subplot_kw=dict(xticks=[], yticks=[])) ax[0].imshow([colors], extent=[0, 10, 0, 1]) ax[1].imshow([grayscale], extent=[0, 10, 0, 1])view_colormap('jet')注意观察灰度图里比较亮的那部分条纹。这些亮度变化不均匀的条纹在灰度图中对应某一段彩色区间,由于色彩太接近容易突显出数据集中不重要的部分,导致眼睛无法识别重点。更好的配色方案是 viridis(已经成为 Matplotlib 2.0 的默认配色方案)。它采用了精心设计的亮度渐变方式,这样不仅便于视觉观察,而且转换为灰度图后更清晰:
view_colormap('viridis')
如果喜欢彩虹效果,可以用 cubehelix配色方案来可视化连续的数值:
view_colormap('cubehelix')
至于其他场景,例如要用两种颜色表示正反两种含义时,可以使用 RdBu 双色配色方案(红色-蓝色),在灰度图上看不到差别:
view_colormap('RdBu')

2. 颜色条刻度的限制与扩展功能的设置
Matplotlib 提供了丰富的颜色条配置功能。由于可以将颜色条本身仅看作是一个 plt.Axes 实例,因此前面所学的有关于坐标轴和刻度值的格式配置技巧都能派上用场。颜色条有一些有趣的特性,例如,我们可以缩短颜色取值的上下限,对于超出上下限的数据,通过 extend 参数用三角箭头表示比上限大的数或者比下限小的数。这种方法很简单,比如你想展示一张噪声图:
# 为图形像素设置1%噪点
speckles = (np.random.random(I.shape) < 0.01)
I[speckles] = (np.random.normal(0, 3, np.count_nonzero(speckles)))
plt.figure(figsize=(10, 3.5))
plt.subplot(1, 2, 1)
plt.imshow(I, cmap='RdBu')
plt.colorbar()
plt.subplot(1, 2, 2)
plt.imshow(I, cmap='RdBu')
plt.colorbar(extend='both')
plt.clim(-1, 1)

左边那副图是用默认的颜色条刻度限制实现的效果,噪点的范围完全覆盖了我们感兴趣的数据。而右边的图形设置了颜色条刻度的上下限,并在上下限之外增加了扩展功能,这样的数据可视化图形显然更有效果。
-
离散型颜色条
最简单的做法就是使用
plt.cm.get_cmap()函数,将适当的配色方案的名称以及需要的区间数量传进去即可:plt.imshow(I, cmap=plt.cm.get_cmap('Blues', 6)) plt.colorbar() plt.clim(-1, 1)
4.9.2 案例:手写数字
数据在 Scikit-Learn 里面,包含近2000份 8 x 8 的手写数字缩略图。
先下载数据,然后用 plt.imshow() 对一些图形进行可视化:
# 加载数字0~5的图形,对其进行可视化
from sklearn.datasets import load_digits
digits = load_digits(n_class=6)
fig, ax = plt.subplots(8, 8, figsize=(6, 6))
for i, axi in enumerate(ax.flat):
axi.imshow(digits.images[i], cmap='binary')
axi.set(xticks=[], yticks=[])

由于每个数字都由 64 像素的色相构成,因此可以将每一个数字看成是一个位于 64 维空间的点,即每个维度表示一个像素的亮度。但是想通过可视化来描述如此高纬度的空间是非常困难的。一种解决方案是通过降维技术,在尽量保留数据内部重要关联性的同时降低数据的维度,例如流形学习,降维是无监督学习的重要内容。
暂且不提具体的降维细节,先来看看如何用流形学习将这些数据投影到二维空间进行可视化:
# 用 IsoMap 方法将数字投影到二维空间
from sklearn.manifold import Isomap
iso = Isomap(n_components=2)
projection = iso.fit_transform(digits.data)
我们将用离散型颜色条显示结果,调整 ticks 与 clim 参数来改善颜色条:
# 画图
plt.scatter(projection[:, 0], projection[:, 1], lw=0.1,
c=digits.target, cmap=plt.cm.get_cmap('cubehelix', 6))
plt.colorbar(ticks=range(6), label='digit value')
plt.clim(-0.5, 5.5)
这个投影还向我们展示了一些数据集的有趣特性。例如,数字 5 和数字 3 在投影中有大面积重叠,说明一些手写的 5 和 3 难以区分,,因此自动分类算法也更容易搞混它们。其他的数字,像数字 1 和 0,隔得特别远,说明两者不太可能出现混淆。
4. 10 多子图
有时候需要从多角度对数据进行对比。Matplotlib 为此提出了子图的概念:在较大的图形中同时放置一组较小的坐标轴。这些子图可能是画中画、网格图,或者是其他更复杂的布局形式。
首先,在 Notebook 中导入画图需要的程序库:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')
import numpy as np
4.10.1 plt.axes:手动创建子图
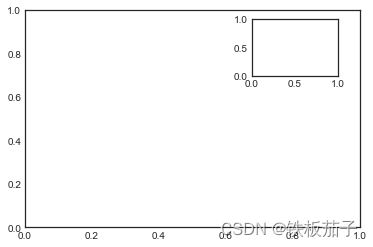
创建坐标轴最基本的方法就是使用 plt.axes 函数。这个函数的默认配置是创建一个标准的坐标轴,填满整张图。它还有一个可选参数,由图形坐标系统的四个值构成。这四个图分别表示图形坐标系统的[bottom, left, width, height](底座表、左坐标、宽度、高度),数值的取值范围是左下角(原点)为 0,右上角为1。
如果想要在右上角创建画中画,那么可以首先将 x 与 y 设置为 0.65(就是将坐标轴原点位于图形高度 65% 和宽度 65% 的位置),然后将 x 与 y 扩展到 0.2(也就是将坐标轴的宽度与高度设置为图形的 20%):
ax1 = plt.axes() # 默认坐标轴
ax2 = plt.axes([0.65, 0.65, 0.2, 0.2])
面向对象画图接口中类似的命令有 fig.add_axes()。用这个命令创建两个竖直排列的坐标轴:
fig = plt.figure()
ax1 = fig.add_axes([0.1, 0.5, 0.8, 0.4],
xticklabels=[], ylim=(-1.2, 1.2))
ax2 = fig.add_axes([0.1, 0.1, 0.8, 0.4],
ylim=(-1.2, 1.2))
x = np.linspace(0, 10)
ax1.plot(np.sin(x))
ax2.plot(np.cos(x));
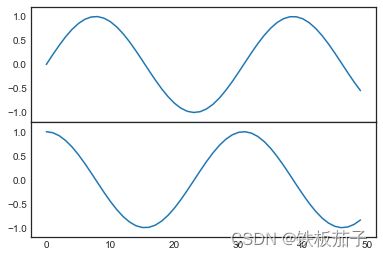
现在就可以看到两个紧凑着的坐标轴(上面的坐标轴没有刻度):上子图(起点 y 坐标为 0.5 位置)与下子图的 x 轴刻度是对应的(起点 y 坐标为 0.1,高度为 0.4)。
4.10.2 plt.subplot:简易网格子图
若干彼此对齐的行列子图是常见的可视化任务,Matplotlib 拥有一些可以轻松创建它们的简便方法。最底层的方法是用 plt.subplot() 在一个网格中创建一个子图。这个命令有三个整型参数——将要创建的网格子图行数、列数和索引值,索引值从 1 开始,从左上角到右下角依次增大:
for i in range(1, 7):
plt.subplot(2, 3, i) # 两行三列
plt.text(0.5, 0.5, str((2, 3, i)),
fontsize=18, ha='center')
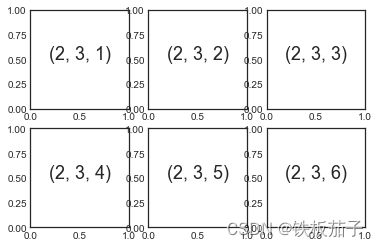
plt.subplots_adjust命令可以调整子图之间的间隔。用面向对象接口的命令 fig.add_subplot()可以取得同样的效果:
fig = plt.figure()
fig.subplots_adjust(hspace=0.4, wspace=0.4)
for i in range(1, 7):
ax = fig.add_subplot(2, 3, i)
ax.text(0.5, 0.5, str((2, 3, i)),
fontsize=18, ha='center')
![]()
我们通过 plt.subplots_adjust的hspace与wspace参数设置与图形高度和宽度一致的子图间距,数值以子图的尺寸为单位,本例中,间距是子图宽度与高度的 40%。
4.10.3 plt.subplots:用一行代码创建网格
创建大型网格子图,想要隐藏内部子图的 x 轴与 y 轴标题时,plt.subplots()可以实现,返回的是一个包含子图的 Numpy 数组。关键参数是行数和列数以及可选参数 sharex 和 sharey,通过它们可以设置不同子图之间的关联关系。
创建一个 2 x 3 网格子图,每行的 3 个子图使用相同的 y 轴坐标,每列的 2 个子图使用相同的 x 轴坐标:
fig, ax = plt.subplots(2, 3, sharex='col', sharey='row')
# 坐标轴存放在一个 NumPy 数组中,按照[row, col]取值
for i in range(2):
for j in range(3):
ax[i, j].text(0.5, 0.5, str((i, j)),
fontsize=18, ha='center')
fig
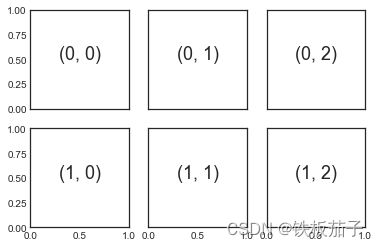
与 plt.subplot()相比,plt.subplots()与 Python 索引从 0 开始的习惯保持一致。
4.10.4 plt.GridSpec:实现更复杂的排列方式
如果想实现不规则的多行多列子图网格,plt.GridSpace() 是最好的工具。plt.GridSpace() 对象本身不能直接创建一个图形,它只是 plt.subplot() 命令可以识别的简易接口。例如,一个带行列间距的 2 x 3 网格的配置代码如下:
grid = plt.GridSpec(2, 3, wspace=0.4, hspace=0.3)
可以通过类似 Python 切片的语法设置子图的位置和扩展尺寸:
plt.subplot(grid[0, 0])
plt.subplot(grid[0, 1:])
plt.subplot(grid[1, :2])
plt.subplot(grid[1, 2]);

这种灵活的网格排列方式用途十分广泛,可以用来创建多轴频次直方图:
# 创建一些正态分布数据
mean = [0, 0]
cov = [[1, 1], [1, 2]]
x, y =np.random.multivariate_normal(mean, cov, 3000).T
# 设置坐标轴和网格配置方式
fig = plt.figure(figsize=(6, 6))
grid = plt.GridSpec(4, 4, hspace=0.2, wspace=0.2)
main_ax = fig.add_subplot(grid[:-1, 1:])
y_hist = fig.add_subplot(grid[:-1, 0], xticklabels=[], sharey=main_ax) # xticklabels 设置x轴刻度标签
x_hist = fig.add_subplot(grid[-1, 1:], yticklabels=[], sharex=main_ax)
# 主坐标轴画散点图
main_ax.plot(x, y, 'ok', markersize=3, alpha=0.2)
#次坐标轴画频次直方图:
x_hist.hist(x, 40, histtype='stepfilled',
orientation='vertical', color='gray')
x_hist.invert_yaxis()
y_hist.hist(y, 40, histtype='stepfilled',
orientation='horizontal', color='gray')
y_hist.invert_xaxis()
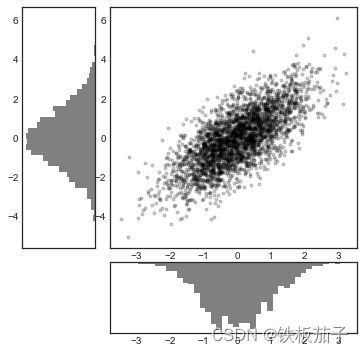
拓展:动态图subplots()和subplot()不同及参数
4.11 文字与注释
最基本的注释类型可能是坐标轴标题与图标题。
可视化一些数据,看看如何通过添加注释来恰当地表达信息。首先导入画图需要用到的函数:
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.style.use('seaborn-whitegrid')
import numpy as np
import pandas as pd
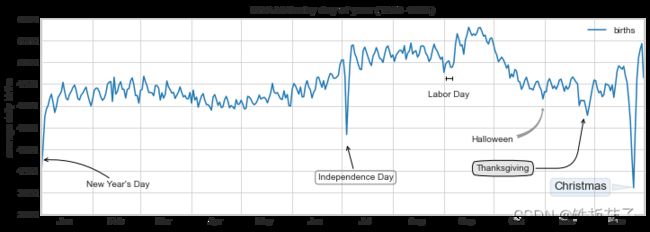
4.11.1 案例:节假日对美国出生率的影响
我们必须对数据做一些清理工作,消除由于输错了日期而造成的异常点(如 6 月 31 号)或者是缺失值(如 1999年 6 月)。消除这些异常的简单方法是直接删除异常值,可以通过更稳定的 sigma 消除法(sigma-clipping,按照正态分布标准差划定范围,SciPy 中默认是四个标准差)操作来实现:
# percentile 计算基于元素排序的统计值
quartiles = np.percentile(births['births'], [25, 50, 75])
mu = quartiles[1]
sig = 0.74 * (quartiles[2] - quartiles[0])
最后一行是样本均值的稳定性估计,其中 0.74 是指标准正态分布的分位数间距。在 query() 方法中用这个范围就可以将有效的生日数据筛选出来了:
births = births.query('(births > @mu - 5 * @sig) & (births < @mu + 5 * @sig)')
然后,将 day 列设置为整数。这列数据在筛选之前是字符串,因为数据集中有的列含有缺失值 ’null‘:
# 将‘day’列设置为整数。由于其中含有缺失值null,因此是字符串
births['day'] = births['day'].astypeype(int)
现在就可以将年月日组合起来创建一个日期索引,这样就可以快速计算每一行是星期几:
# 从年月日创建一个日期索引
births.index = pd.to_datetime(10000 * births.year +
100 * births.month +
births.day, format='%Y%m%d')
每个年份平均每天的出生人数,可以按照月和日两个维度分别对数据进行分组:
births_by_date = births.pivot_table('births',
[births.index.month, births.index.day])
births_by_date.index = [datetime(2012, month, day)
for (month, day) in births_by_date.index]
fig, ax = plt.subplots(figsize=(12, 4))
births_by_date.plot(ax=ax);
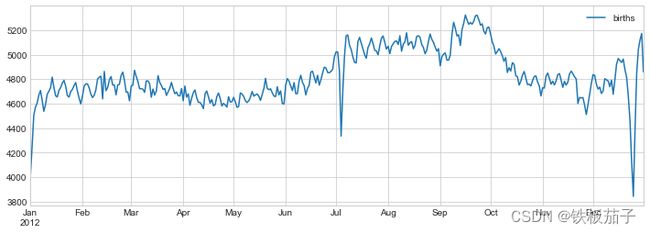
在用这样的图表达时,如果可以在图中增加一些注释,就能吸引更多读者的注意。可以通过plt.text / ax.text命令手动添加注释,它们可以在具体的 x / y 坐标点上放上文字:
fig, ax = plt.subplots(figsize=(12, 4))
births_by_date.plot(ax=ax)
#在图上增加文字标签
style = dict(size=10, color='gray')
ax.text('2012-1-1', 3950, "New Year's Day", **style)
ax.text('2012-7-4', 4250, "Independence Day", ha='center', **style)
ax.text('2012-9-4', 4850, "Labor Day", ha='center', **style)
ax.text('2012-10-31', 4600, "Halloween Day", ha='right', **style)
ax.text('2012-11-25', 4450, "Thanksgiving Day", ha='center', **style)
ax.text('2012-12-25', 3850, "Christmas Day", ha='right', **style)
# 设置坐标轴标题
ax.set(title='USA births by day of year (1969-1988)',
ylabel='average daily births')
# 设置x轴刻度值,让月份居中显示
ax.xaxis.set_major_locator(mpl.dates.MonthLocator())
ax.xaxis.set_minor_locator(mpl.dates.MonthLocator(bymonthday=15))
ax.xaxis.set_major_formatter(plt.NullFormatter())
ax.xaxis.set_minor_formatter(mpl.dates.DateFormatter('%h'));
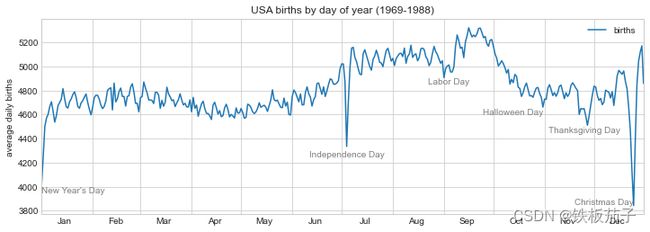
ax.text方法需要一个 x 轴坐标、一个 y 轴坐标、一个字符串和一些可选参数,比如文字的颜色、字号、对齐方式以及其他文字的属性。这里用了ha='right'与ha='center',ha 是水平对齐方式的缩写。
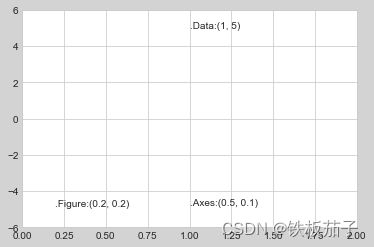
4.11.2 坐标变换与文字位置
前面的示例将文字放在了目标数据的位置上。但是有时候可能需要将文字放在与数据无关的位置上,比如坐标轴或图形中。在 Matplotlib 中,我们通过调整坐标变换来实现。
任何图形显示框架都需要一些变换坐标系的机制。例如,当一个位于(x, y)=(1, 1)位置的点需要以某种方式显示在图上特定的位置时,就需要屏幕的像素来表示。用数学方法处理这些数据变换很简单,Matplotlib 有一组非常棒的工具可以实现类似的功能(这些工具位于 matplotlib.transforms 子模块中)。
一共有三种解决这类问题的预定义变换方式:
ax.transData:以数据为基准的坐标变换。
ax.transAxes:以坐标轴为基准的坐标变换(以坐标轴维度为单位)。
fig.transFigure:以图形为基准的坐标变换(以图形维度为单位)。
下面举一个例子,用三种变换方式将文字画在不同位置:
fig, ax = plt.subplots(facecolor='lightgray')
ax.axis([0, 10, 0, 10])
# 虽然 transform=ax.transData 是默认值,但还是设置一下
ax.text(1, 5, ".Data:(1, 5)", transform=ax.transData)
ax.text(0.5, 0.1, ".Axes:(0.5, 0.1)", transform=ax.transAxes)
ax.text(0.2, 0.2, ".Figure:(0.2, 0.2)", transform=fig.transFigure);

默认情况下,上面的文字在默认坐标系中是对齐的,这三个字符串开头的 · 字符基本就是对应的坐标位置。
transData坐标用 x 轴与 y 轴的标签作为数据的坐标。transAxes坐标以坐标轴(图中白色的矩形)左下角的位置为原点按坐标轴尺寸的比例呈现坐标。transFigure坐标与之类似,不过是以图形(图中灰色矩形)左下角的位置为原点,按图形尺寸的比例呈现坐标。
需要注意的是,假如改变了坐标轴上下限,那么只有transData坐标会受影响,其他坐标系都不变:
ax.set_xlim(0, 2)
ax.set_ylim(-6, 6)
fig
如果是 Notebook 中运行,只需要把%matplotlib inline改成%matplotlib notebook就可以实现交互。
4.11.3 箭头与注释
除了刻度线和文字,简单的箭头也是一种有用的注释标签。
在 Matplotlib 里面画箭头通常比你想象的困难。plt.annotate()函数既可以创建文字也可以创建箭头,而且它创建的箭头能进行非常灵活的配置。
下面用 annotate 的一些配置选项来演示:
%matplotlib inline
fig, ax = plt.subplots()
x = np.linspace(0, 20, 1000)
ax.plot(x, np.cos(x))
ax.axis('equal')
ax.annotate('local maximum', xy=(6.28, 1), xytext=(10, 4),
arrowprops=dict(facecolor='black', shrink=0.05))
ax.annotate('local minimum', xy=(5 * np.pi, -1), xytext=(2, -6),
arrowprops=dict(arrowstyle="->",
connectionstyle="angle3,angleA=0,angleB=-90"));

箭头的风格是通过 arrowprops 字典控制的,里面有许多可用的选项。用前面美国出生人数图来演示一些箭头注释:
fig, ax = plt.subplots(figsize=(12, 4))
births_by_date.plot(ax=ax)
# 在图上增加箭头标签
ax.annotate("New Year's Day", xy=('2012-1-1', 4100), xycoords='data',
xytext=(50, -30), textcoords='offset points',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3,rad=0.2"))
ax.annotate("Independence Day", xy=('2012-7-4', 4250), xycoords='data',
bbox=dict(boxstyle="round", fc="none", ec="gray"),
xytext=(10, -40), textcoords='offset points', ha='center',
arrowprops=dict(arrowstyle="->"))
ax.annotate('Labor Day', xy=('2012-9-4', 4850), xycoords='data', ha='center',
xytext=(0, -20), textcoords='offset points')
ax.annotate('', xy=('2012-9-1', 4850), xytext=('2012-9-7', 4850),
xycoords='data', textcoords='data',
arrowprops={'arrowstyle': '|-|,widthA=0.2,widthB=0.2',})
ax.annotate('Halloween', xy=('2012-10-31', 4600), xycoords='data',
xytext=(-80, -40), textcoords='offset points',
arrowprops=dict(arrowstyle="fancy",
fc="0.6", ec="none",
connectionstyle="angle3,angleA=0,angleB=-90"))
ax.annotate('Thanksgiving', xy=('2012-11-25', 4500), xycoords='data',
xytext=(-120, -60), textcoords='offset points',
bbox=dict(boxstyle="round4,pad=.5", fc="0.9"),
arrowprops=dict(arrowstyle="->",
connectionstyle="angle,angleA=0,angleB=80,rad=20"))
ax.annotate('Christmas', xy=('2012-12-25', 3850), xycoords='data',
xytext=(-30, 0), textcoords='offset points',
size=13, ha='right', va="center",
bbox=dict(boxstyle="round", alpha=0.1),
arrowprops=dict(arrowstyle="wedge,tail_width=0.5", alpha=0.1));
# 设置坐标轴标题
ax.set(title='USA births by day of year (1969-1988)',
ylabel='average daily births')
# 设置 x 轴刻度值,让月份居中显示
ax.xaxis.set_major_locator(mpl.dates.MonthLocator())
ax.xaxis.set_minor_locator(mpl.dates.MonthLocator(bymonthday=15))
ax.xaxis.set_major_formatter(plt.NullFormatter())
ax.xaxis.set_minor_formatter(mpl.dates.DateFormatter('%h'));
ax.set_ylim(3600, 5400);
4.12 自定义坐标轴刻度
locator坐标轴定位器,formatter 格式生成器。
每个 axes 都有 xaxis 和 yaxis 属性,每个属性同样包含构成坐标轴的线条、刻度和标签的全部属性。
4.12.1 主要刻度与次要刻度
主要刻度是更大、更显著,而次要刻度往往更小,虽然一般情况下,Matplotlib 不会使用次要刻度,但是会在对数图中看到它们:
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
import numpy as np
ax = plt.axes(xscale='log', yscale='log')
![]()
可以通过设置每个坐标轴的 formatter 与 locator 对象,自定义这些刻度属性(包括刻度线的位置和标签)。来检查一下图形 x 轴的属性:
print(ax.xaxis.get_major_locator())
print(ax.xaxis.get_minor_locator())
<matplotlib.ticker.LogLocator object at 0x00000229B4E1D250>
<matplotlib.ticker.LogLocator object at 0x00000229B4E12C10>
print(ax.xaxis.get_major_formatter())
print(ax.xaxis.get_minor_formatter())
<matplotlib.ticker.LogFormatterSciNotation object at 0x00000229B4E1E970>
<matplotlib.ticker.LogFormatterSciNotation object at 0x00000229B4E12250>
4.12.2 隐藏刻度与标签
最常用的刻度/标签格式化操作可能就是隐藏刻度与标签了,可以通过 plt.NullLocator() 与 plt.NullFormatter() 来实现:
ax = plt.axes()
ax.plot(np.random.rand(50))
ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_formatter(plt.NullFormatter())

需要注意的是,我们移除了 x 轴标签(但是保留了刻度线/网格线),以及 y 轴的刻度(标签也一并被移除)。许多场景中不需要刻度线,比如想显示一组图像时:
fig, ax = plt.subplots(5, 5, figsize=(5, 5))
fig.subplots_adjust(hspace=0, wspace=0) # `plt.subplots_adjust`命令可以调整子图之间的间隔。
# 从 scikit-learn 获取一些人脸照片数据
from sklearn.datasets import fetch_olivetti_faces
faces = fetch_olivetti_faces().images
for i in range(5):
for j in range(5):
ax[i, j].xaxis.set_major_locator(plt.NullLocator())
ax[i, j].yaxis.set_major_locator(plt.NullLocator())
ax[i, j].imshow(faces[10 * i + j], cmap="bone")

需要注意的是,由于每幅人脸图形默认都有自己的坐标轴,然而在这幅特殊化的场景中,刻度值(本例是像素)的存在并不能传达任何有用的信息,因此需要将定位器设置为空。
4.12.3 增加刻度数量
默认刻度标签有一个问题,就是显示较小图形时,通常刻度显得十分拥挤,比如:
fig, ax = plt.subplots(4, 4, sharex=True, sharey=True)

我们可以通过plt.MaxNLocator()来解决这个问题,通过它可以设置最多需要显示多少刻度。根据设置最多的刻度数量,Matplotlib 会自动为刻度安排恰当的位置:
# 为每个坐标轴设置主要刻度定位器
for axi in ax.flat:
axi.xaxis.set_major_locator(plt.MaxNLocator(3))
axi.yaxis.set_major_locator(plt.MaxNLocator(3))
fig
4.12.4 花哨的刻度格式
扩展:
plt.plot(x, y, ls="-", lw=2, label="plot figure")
- x: x轴上的数值
- y: y轴上的数值
- ls:折线图的线条风格
- lw:折线图的线条宽度
- label:标记图内容的标签文本
# 画正弦函数和余弦函数
fig, ax = plt.subplots()
x = np.linspace(0, 3 * np.pi, 1000)
ax.plot(x, np.sin(x), lw=3, label='Sine')
ax.plot(x, np.cos(x), lw=3, label='Cosine')
# 设置网格、图例和坐标轴上下限
ax.grid(True) # 是否显示网格线
# 在图上标明一个图例,用于说明每条曲线的文字显示,
# legend()有一个loc参数,用于控制图例的位置。 比如 plot.legend(loc=2) , 这个位置就是4象项中的第二象项,也就是左上角。
# loc可以为1,2,3,4 这四个数字。如果把那句legend() 的语句去掉,那么图形上的图例也就会消失了。
ax.legend(frameon=False)
ax.axis('equal')
ax.set_xlim(0, 3 * np.pi);
![]()
改变一下这幅图,将刻度线与网格线画在 π 的倍数上,图形会更加自然。可以通过设置一个 MultipleLocator 来实现,它可以将刻度放在提供的数值的倍数上,为了更好的测量,在 π/4 的倍数上添加主要刻度和次要刻度:
ax.xaxis.set_major_locator(plt.MultipleLocator(np.pi/2))
ax.xaxis.set_minor_locator(plt.MultipleLocator(np.pi/4))
fig
用自定义的函数设置不同刻度标签的显示:
def format_func(value, tick_number):
# 找到 π/2 的倍数刻度
N = int(np.round(2 * value / np.pi)) # np.round()函数取整
if N == 0:
return "0"
elif N == 1:
return r"$\pi/2$"
elif N == 2:
return r"$\pi$"
elif N % 2 > 0:
return r"${0}\pi/2$".format(N)
else:
return r"${0}\pi$".format(N // 2)
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
fig
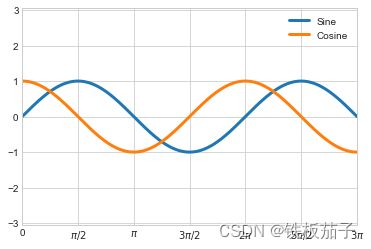
在数学表达式两侧加上美元符号($),这样就可以方便显示数学符号和数学公式。
plt.FuncFormatter()不仅可以为自定义图形刻度提供十分灵活的功能,而且用法非常简单。
4.12.5 格式生成器与定位器小结
以下的所有类都在 plt 命名空间内:
| 定位器类 | 描述 |
|---|---|
| NullLocator | 无刻度 |
| FixedLocator | 刻度位置固定 |
| IndexLocator | 用索引作为定位器(如 x = range(len(y))) |
| LinearLocator | 从 min 到 max 均匀分布刻度 |
| LogLocator | 从 min 到 max 按对数分布刻度 |
| MultipleLocator | 刻度和范围都是基数(base)的倍数 |
| MaxNLocator | 为最大刻度找到最优位置 |
| AutoLocator | (默认) 以 MaxNLocator 进行简单配置 |
| AutoMinorLocator | 次要刻度的定位器 |
| 格式生成器类 | 描述 |
|---|---|
| NullFormatter | 刻度上无标签 |
| IndexFormatter | 将一组标签设置为字符串 |
| FixedFormatter | 手动为刻度设置标签 |
| FuncFormatter | 用自定义函数设置标签 |
| FormatStrFormatter | 为每个刻度值设置字符串格式 |
| ScalarFormatter | (默认) 为标量值设置标签 |
| LogFormatter | 对数坐标轴的默认格式生成器 |
4.13 Matplotlib 自定义:配置文件与样式表
4.13.1 手动配置图形
import matplotlib.pyplot as plt
plt.style.use('classic')
import numpy as np
%matplotlib inline
Matplotlib 默认配置的频次直方图
x = np.random.randn(1000)
plt.hist(x);
# 用灰色背景
ax = plt.axes(fc='#E6E6E6')
ax.set_axisbelow(True)
# 画上白色的网格线
plt.grid(color='w', linestyle='solid') # 实线
# 隐藏坐标轴的线条
for spine in ax.spines.values():
spine.set_visible(False)
# 隐藏上边与右边的刻度
ax.xaxis.tick_bottom()
ax.yaxis.tick_left()
# 弱化刻度和标签
ax.tick_params(colors='gray', direction='out')
for tick in ax.get_xticklabels():
tick.set_color('gray')
for tick in ax.get_yticklabels():
tick.set_color('gray')
# 设置频次直方图轮廓色与填充色
ax.hist(x, edgecolor='#E6E6E6', color='#EE6666');
4.13.2 修改默认配置:rcParams
Matplotlib 每次加载时,都会自定义一个运行时配置(rc),其中包含所有你创建的图形元素的默认分隔。你可以用 plt.rc 简便方法随时修改这个配置。
先复制一下目前的 rcParams 字典,这样可以在修改之后再还原回来:
Ipython_default = plt.rcParams.copy()
现在可以用 plt.rc 函数来修改配置参数了:
from matplotlib import cycler
colors = cycler('color',
['#EE6666', '#3388BB', '#9988DD',
'#EECC55', '#88BB44', '#FFBBBB'])
plt.rc('axes', facecolor='#E6E6E6', edgecolor='none',
axisbelow=True, grid=True, prop_cycle=colors)
plt.rc('grid', color='w', linestyle='solid')
plt.rc('xtick', direction='out', color='gray')
plt.rc('ytick', direction='out', color='gray')
plt.rc('patch', edgecolor='#E6E6E6')
plt.rc('lines', linewidth=2)
完成后,来创建一个效果图:
plt.hist(x);
![]()
再画一些线图看看 rc 的效果:
for i in range(4):
plt.plot(np.random.rand(10))
plt.rcParams = Ipython_default
4.13.3 样式表
有一个很好用的style模块,包含大量的新式默认样式表。
通过plt.style.available命令可以看到所有可用的风格:
plt.style.available[:]
['Solarize_Light2',
'_classic_test_patch',
'_mpl-gallery',
'_mpl-gallery-nogrid',
'bmh',
'classic',
'dark_background',
'fast',
'fivethirtyeight',
'ggplot',
'grayscale',
'seaborn',
'seaborn-bright',
'seaborn-colorblind',
'seaborn-dark',
'seaborn-dark-palette',
'seaborn-darkgrid',
'seaborn-deep',
'seaborn-muted',
'seaborn-notebook',
'seaborn-paper',
'seaborn-pastel',
'seaborn-poster',
'seaborn-talk',
'seaborn-ticks',
'seaborn-white',
'seaborn-whitegrid',
'tableau-colorblind10']
使用某种样式表的基本方法如下所示:
plt.style.use('stylename')
但需要注意的是,这样会改变后面所有的风格!如果需要,你可以使用风格上下文管理器(context manager) 临时更换至另一种风格:
with plt.style.context('stylename'):
make_a_plot()
来创建一个可以画两种基本图形的函数:
def hist_and_lines():
np.random.seed(0)
fig, ax = plt.subplots(1, 2, figsize=(11, 4))
ax[0].hist(np.random.rand(1000))
for i in range(3):
ax[1].plot(np.random.rand(10))
ax[1].legend(['a', 'b', 'c'], loc='lower left')
下面用这个函数演示不同风格的显示效果:
-
默认风格
首先,将之前设置的运行时配置还原成默认配置:
# 重置 rcParams plt.rcParams.update(Ipython_default);默认风格的效果:
hist_and_lines() -
Five ThirtyEight 风格
Five ThirtyEight 风格模仿的是著名网站 FiveThirtyEight 的绘图风格。使用深色的线条和透明的坐标轴:
with plt.style.context('fivethirtyeight'): hist_and_lines() -
ggplot 风格
R 语言的 ggplot 是非常流行的可视化工具,Matplotlib 的 ggplot 风格就是模仿这个程序包的默认风格:
with plt.style.context('ggplot'): hist_and_lines() -
bmh 风格
with plt.style.context('bmh'): hist_and_lines() -
黑色背景风格
with plt.style.context('dark_background'): hist_and_lines() -
灰度风格
with plt.style.context('grayscale'): hist_and_lines()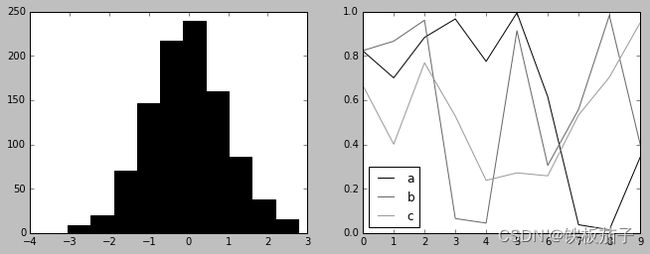
-
Seaborn 风格(推荐使用)
import seaborn as sns sns.set() hist_and_lines()
4.14 用 Matplotlib 画三维图
导入 Matplotlib 自带的 mplot3d 工具箱画三维图:
from mpl_toolkits import mplot3d
导入这个子模块之后,就可以在创建任意一个普通坐标的过程加入 projection=‘3d’ 关键字,从而创建一个三维坐标轴:
fig = plt.figure()
ax = plt.axes(projection='3d')
可以用%matplotlib notebook在 Notebook 中交互浏览。
4.14.1 三维数据点与线
三维函数的参数与前面介绍过的二维函数基本相同。
画一个三角螺旋线,在线上随机分布一些散点:
ax = plt.axes(projection='3d')
#三维线的数据
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')
#三维散点的数据
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');
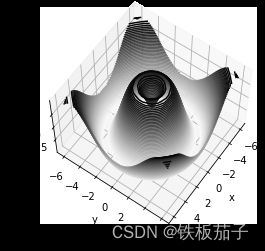
4.14.2 三维等高线图
与二维 ax.contour图形一样,ax.contour3D要求所有数据都是二维网格数据的形式,并且由函数计算 z 轴的数值。
用三维正弦函数画的三维等高线图:
def f(x, y):
return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6, 6, 30)
y = np.linspace(-6, 6, 30)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z');
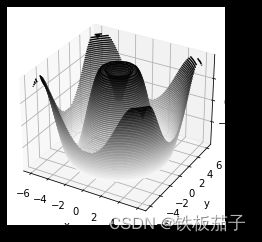
默认观察视角不是最优的,view_init可以调整观察角度与方位角。
在这个示例中,我们把俯仰角调整为 60 度(这里的 60 度是 x-y 平台的旋转角度),方位角调整为 35 度(就是绕 z 轴顺时针旋转 35 度):
ax.view_init(60, 35)
fig
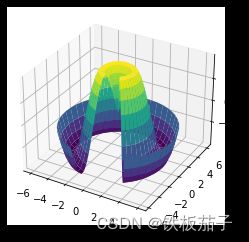
4.14.3 线框图和曲面图
线框图和曲面图都是将网格数据映射成三维曲面,得到的三维形状很容易可视化。
fig = plt.figure()
ax = plt.axes(projection='3d')
ax.plot_wireframe(X, Y, Z, color='black')
ax.set_title('wireframe');
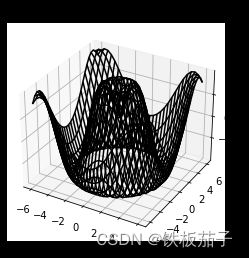
曲面图与线框图类似,只不过线框图的每个面都是由多边形构成的。只要增加一个配色方案来填充这些多边形,就可以让读者感受到可视化图形表面的拓扑结构了:
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none')
ax.set_title('surface');
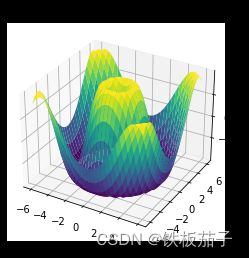
注意的是,画曲面图需要二维数据,但可以不是直角坐标系(也可以用极坐标系)。下面的示例创建了一个局部的极坐标网格(polar grid),当我们把它画成 surface3D 图形时,可以获得一种使用了切片的可视化效果:
r = np.linspace(0, 6, 20)
theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)
X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1,
cmap='viridis', edgecolor='none');
4.14.4 曲面三角剖分
在某些应用场景中 ,上述这些要求均匀采样的网格数据太过严格且不太容易实现。这时就可以使用三角剖分图形。如果没有笛卡尔或极坐标网格的均匀绘制图形,我们该如何同一组随机数画图呢?
theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta)) # ravel()方法将数组维度拉成一维数组
y = np.ravel(r * np.cos(theta))
z = f(x, y)
可以先为数据创建一个散点图,对将要采样的图形有一个基本的认识:
ax = plt.axes(projection='3d')
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5);
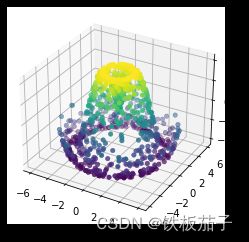
过有许多地方需要修补,这些工作有ax.plot_trisurf函数帮助我们完成。它首先找到一组所有点都连接起来的三角形,然后用这些三角形创建曲面(其中 x, y, z 都是一维数组):
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z,
cmap='viridis', edgecolor='none');
虽然结果肯定没有之前用均匀网格画的图完美,但是这种三角剖分方法很灵活,可以创建各种有趣的三维图。例如,可以用它画一条三维的莫比乌斯带:
案例:莫比乌斯带
莫比乌斯带是把一根纸条旋转180度后,再把两头粘起来做的纸带圈。拓扑学的角度看它只有一个面,由于它是一条二维带,因此需要两个内在维度。一个维度取值范围是 0~2π,另一个维度取值范围是 -1~1,表示莫比乌斯带的宽度:
theta = np.linspace(0, 2 * np.pi, 30)
w = np.linspace(-0.25, 0.25, 8)
w, theta = np.meshgrid(w, theta)
确定带上每个点坐标(x, y, z),我们可能找到两种旋转关系,一种是圆圈绕着圆心旋转,另一种是莫比乌斯带在自己的坐标轴上旋转。因此,对于一条莫比乌斯带,我们必然会有环的一半旋转 180 度。
phi = 0.5 * theta
现在我们将极坐标转化为三维直角坐标。定义每个点到中心的距离(半径)r,那么直角坐标(x, y, z)就是:
# x - y 平面内的半径
r = 1 + w * np.cos(phi)
x = np.ravel(r * np.cos(theta))
y = np.ravel(r * np.sin(theta))
z = np.ravel(w * np.sin(phi))
最后,要画出莫比乌斯带,还必须保证三角剖分是正确的,最好的实现方法就是首先用基本参数化方法定义三角剖分,然后用 Matplotlib 将三角剖分映射到莫比乌斯带的三维空间里,这样就可以画出图形:
# 用基本参数化方法定义三角剖分
from matplotlib.tri import Triangulation
tri = Triangulation(np.ravel(w), np.ravel(theta))
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, triangles=tri.triangles,
cmap='viridis', linewidths=0.2);
ax.set_xlim(-1, 1); ax.set_ylim(-1, 1); ax.set_zlim(-1, 1);
4.15 用 Basemap 可视化地图数据
地图数据可视化是数据科学中一种十分常见的可视化类型。Matplotlib 做此类可视化的主要工具是 Basemap 工具箱,它是 Matplotlib 的 mpl_toolkits 命名空间里的众多工具箱之一。
安装 Basemap:
conda install basemap
只需要在标准导入模块增加一行即可:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap
4.16 用 Seaborn 做数据可视化
Matplotlib 的三大缺点:
- Matplotlib 2.0 之前的版本默认配置样式绝不是用户的最佳选择。
- Matplotlib 的 API 比较底层。
- 由于 Matplotlib 比 Pandas 早十几年,所以并不是为了 Pandas 的 DataFrame 设计的。
Seaborn 在 Matplotlib 的基础上开发了一套 API,为默认的图形样式和颜色设置提供了理智的选择,为常用的统计图形定义了很多简单的高级函数,并与 Pandas DataFrame 的功能有机结合。
4.16.1 Seaborn 与 Matplotlib
用 Matplotlib 的经典图形样式和配色方案画一个简易的游走图:
import matplotlib.pyplot as plt
plt.style.use('classic')
import numpy as np
import pandas as pd
# 创建一些游走数据
rng = np.random.RandomState(0)
x = np.linspace(0, 10, 500)
y = np.cumsum(rng.randn(500, 6), 0) # 求数组的所有元素的累计和,可通过参数axis指定求某个轴向的统计值。
# 用 Matplotlib 默认样式画图
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
import seaborn as sns
sns.set()
plt.plot(x, y)
plt.legend('ABCDEF', ncol=2, loc='upper left');
4.16.2 Seaborn 图形介绍
Seaborn 的主要思想使是用高级命令为统计数据探索和统计模型拟合创建各种图形。Matplotlib 就是 Seaborn 的底层,但是用 Seaborn API 会更方便。
-
频次直方图、KDE 和密度图
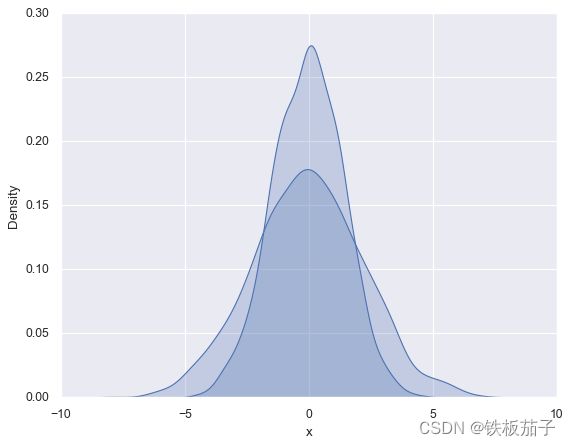
频次直方图:data = np.random.multivariate_normal([0, 0], [[5, 2], [2, 2]], size=2000) # 二维正态分布 data = pd.DataFrame(data, columns=['x', 'y']) for col in 'xy': plt.hist(data[col], density=True, alpha=0.5)for col in 'xy': sns.kdeplot(data[col], shade=True)sns.displot(data['x']) sns.displot(data['y']);
sns.kdeplot(data);
二维 KDE 联合分布图:
with sns.axes_style('white'):
sns.jointplot(x='x', y='y', data=data, kind='kde');
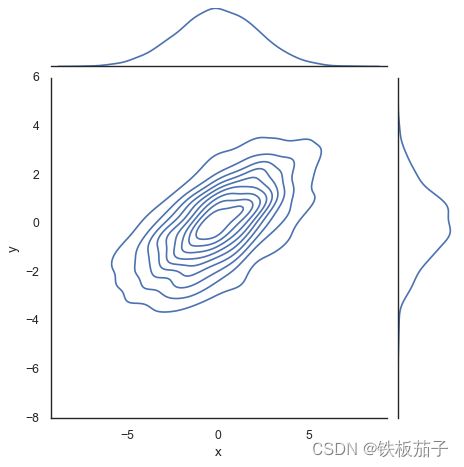
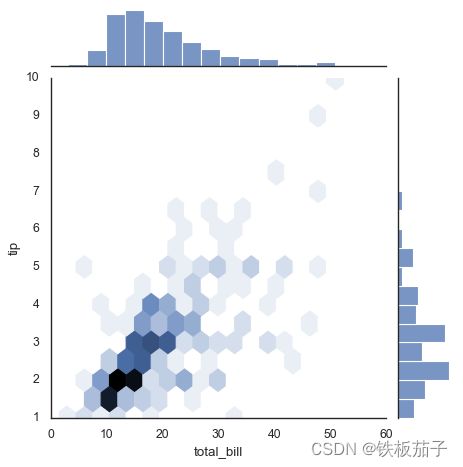
可以向jointplot函数传递一些参数,例如,可以使用六边形快代替频次直方图:
with sns.axes_style('white'):
sns.jointplot(x="x", y="y", data=data, kind='hex');
-
矩阵图
当你需要对多维数据进行可视化需要使用矩形图。如果想画出所有变量中任意两个变量之间的图形,用矩形图探索多维数据不同维度间的相关性非常有效。
鸢尾花花瓣与花萼数据:
iris = pd.read_csv('data/iris.csv') iris.head()sepal_length sepal_width petal_length petal_width species 0 5.1 3.5 1.4 0.2 setosa 1 4.9 3.0 1.4 0.2 setosa 2 4.7 3.2 1.3 0.2 setosa 3 4.6 3.1 1.5 0.2 setosa 4 5.0 3.6 1.4 0.2 setosa 可视化样本中多个维度关系非常简单,直接用
sns.pairplot即可:sns.pairplot(iris, hue='species', height=2.5); -
分面频次直方图
有时观察数据最好的方法就是借助数据子图的频次直方图。Seaborn 的
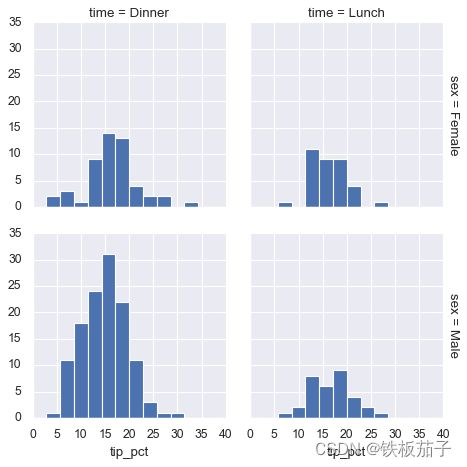
FacetGrid(即分面频次直方图)让这件事变得简单起来。某个餐厅统计的服务员收小费的数据:
tips = pd.read_csv('data/tips.csv') tips.head()total_bill tip sex smoker day time size 0 16.99 1.01 Female No Sun Dinner 2 1 10.34 1.66 Male No Sun Dinner 3 2 21.01 3.50 Male No Sun Dinner 3 3 23.68 3.31 Male No Sun Dinner 2 4 24.59 3.61 Female No Sun Dinner 4 tips['tip_pct'] = 100 * tips['tip'] / tips['total_bill'] grid = sns.FacetGrid(tips, row="sex", col="time", margin_titles=True) grid.map(plt.hist, "tip_pct", bins=np.linspace(0, 40, 15)); -
因子图
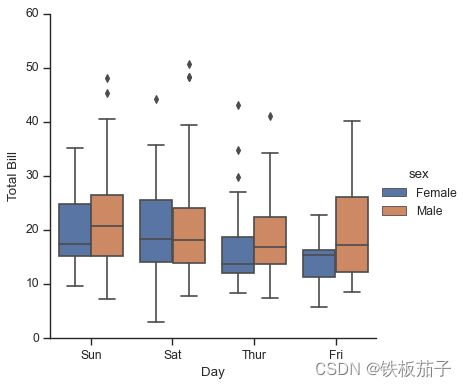
因子图也是对数据子集进行可视化的方法。可以通过它观察一个参数在另一个参数间隔中的分布情况:
with sns.axes_style(style='ticks'): # sns.catplot() 函数用于绘制两维变量的关系图,也就是共用x坐标,按照hue分组,画出不同 y 的值 # 参数kind:point默认,bar柱形图,count频次,box箱体,violin提琴,strip散点,swarm分散点 g = sns.catplot(x="day", y="total_bill", hue="sex", data=tips, kind="box") g.set_axis_labels("Day", "Total Bill"); -
联合分布
可以用
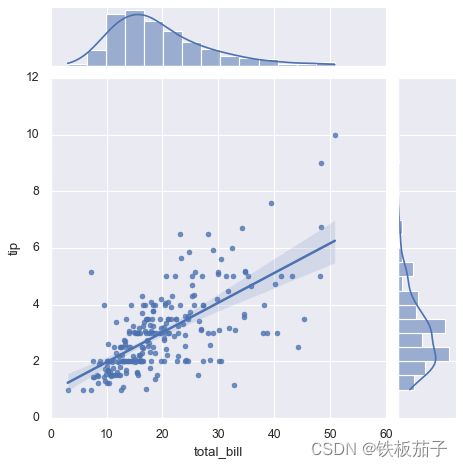
sns.jointplot画出不同数据集的联合分布和各数据本身的分布:with sns.axes_style('white'): sns.jointplot(x="total_bill", y="tip", data=tips, kind='hex')sns.jointplot(x="total_bill", y="tip", data=tips, kind='reg'); -
条形图
时间序列可以用
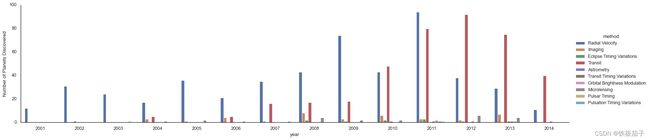
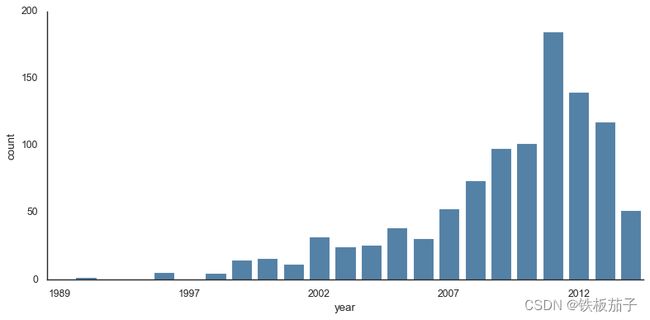
sns,factorplot画出条形图。planets = pd.read_csv('data/planets.csv') planets.head()method number orbital_period mass distance year 0 Radial Velocity 1 269.300 7.10 77.40 2006 1 Radial Velocity 1 874.774 2.21 56.95 2008 2 Radial Velocity 1 763.000 2.60 19.84 2011 3 Radial Velocity 1 326.030 19.40 110.62 2007 4 Radial Velocity 1 516.220 10.50 119.47 2009 with sns.axes_style('white'): g = sns.catplot(x="year", data=planets, aspect=4.0, kind='count', hue='method', order=range(2001, 2015)) g.set_ylabels('Number of Planets Discovered')with sns.axes_style('white'): g = sns.catplot(x="year", data=planets, aspect=2, kind='count', color='steelblue') g.set_xticklabels(step=5)
4.16.3 案例:探索马拉松比赛成绩数据
data = pd.read_csv('data/marathon-data.csv')
data.head()
| age | gender | split | final | |
|---|---|---|---|---|
| 0 | 33 | M | 01:05:38 | 02:08:51 |
| 1 | 32 | M | 01:06:26 | 02:09:28 |
| 2 | 31 | M | 01:06:49 | 02:10:42 |
| 3 | 38 | M | 01:06:16 | 02:13:45 |
| 4 | 31 | M | 01:06:32 | 02:13:59 |
默认情况下,Pandas 会把时间加载为 Python 字符串格式(类型是 object)。可以用 DataFrame 的dtypes属性查看:
data.dtypes
age int64
gender object
split object
final object
dtype: object
写一个把字符串转化为时间类型的函数:
from datetime import datetime
def convert_time(s):
h, m, s = map(int, s.split(':'))
return pd.Timedelta(hours=h, minutes=m, seconds=s)
data = pd.read_csv('data/marathon-data.csv',
converters={'split':convert_time, 'final':convert_time})
data.head()
| age | gender | split | final | |
|---|---|---|---|---|
| 0 | 33 | M | 0 days 01:05:38 | 0 days 02:08:51 |
| 1 | 32 | M | 0 days 01:06:26 | 0 days 02:09:28 |
| 2 | 31 | M | 0 days 01:06:49 | 0 days 02:10:42 |
| 3 | 38 | M | 0 days 01:06:16 | 0 days 02:13:45 |
| 4 | 31 | M | 0 days 01:06:32 | 0 days 02:13:59 |
data.dtypes
age int64
gender object
split timedelta64[ns]
final timedelta64[ns]
dtype: object
为了使用 Seaborn 画图,还需要添加一行,将时间换算成秒:
data['split_sec'] = data['split'].astype(np.int64) / 1E9
data['final_sec'] = data['final'].astype(np.int64) / 1E9
data.head()
| age | gender | split | final | split_sec | final_sec | |
|---|---|---|---|---|---|---|
| 0 | 33 | M | 0 days 01:05:38 | 0 days 02:08:51 | 3938.0 | 7731.0 |
| 1 | 32 | M | 0 days 01:06:26 | 0 days 02:09:28 | 3986.0 | 7768.0 |
| 2 | 31 | M | 0 days 01:06:49 | 0 days 02:10:42 | 4009.0 | 7842.0 |
| 3 | 38 | M | 0 days 01:06:16 | 0 days 02:13:45 | 3976.0 | 8025.0 |
| 4 | 31 | M | 0 days 01:06:32 | 0 days 02:13:59 | 3992.0 | 8039.0 |
现在通过jointplot函数画图,从而对数据有个认识:
with sns.axes_style('white'):
g = sns.jointplot(x="split_sec", y="final_sec", data=data, kind="hex")
g.ax_joint.plot(np.linspace(4000, 16000),
np.linspace(8000, 32000), ':k')

图中的实点线表示一个人全程保持一个速度跑完马拉松,即上半程与下半程耗时相同。然而实际的成绩分布表明,绝大多数人都是越往后跑越慢,
创造一列(split_frac, split fraction)来表示前后半程的差异,衡量比赛选手后半程加速或前半程加速的程度:
data['split_frac'] = 1 - 2 * data['split_sec'] / data['final_sec']
data.head()
| age | gender | split | final | split_sec | final_sec | split_frac | |
|---|---|---|---|---|---|---|---|
| 0 | 33 | M | 0 days 01:05:38 | 0 days 02:08:51 | 3938.0 | 7731.0 | -0.018756 |
| 1 | 32 | M | 0 days 01:06:26 | 0 days 02:09:28 | 3986.0 | 7768.0 | -0.026262 |
| 2 | 31 | M | 0 days 01:06:49 | 0 days 02:10:42 | 4009.0 | 7842.0 | -0.022443 |
| 3 | 38 | M | 0 days 01:06:16 | 0 days 02:13:45 | 3976.0 | 8025.0 | 0.009097 |
| 4 | 31 | M | 0 days 01:06:32 | 0 days 02:13:59 | 3992.0 | 8039.0 | 0.006842 |
如果前后半程差异系数小于0,就表示这个人是后半程加速型选手。
差异系数分布图:
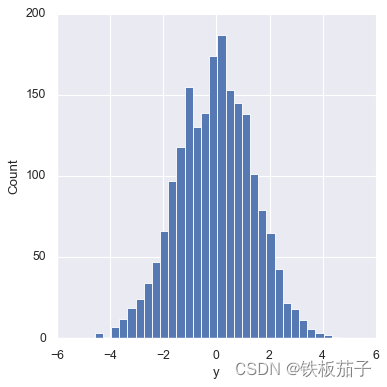
sns.displot(data['split_frac'], kde=False);
plt.axvline(0, color="k", linestyle="--");
sum(data.split_frac < 0)
251
在大约 4 万人的马拉松比赛选手中,只有大概 250 人能做到后半程加速。
现在看看前后半程差异系数与其他变量有没有相关性。用一个矩阵图pairfrid画出所有变量间的相关性:
g = sns.PairGrid(data, vars=['age', 'split_sec', 'final_sec', 'split_frac'],
hue='gender', palette='RdBu_r')
g.map(plt.scatter, alpha=0.8)
g.add_legend();

从图中可以看出,虽然前后半程差异系数与年龄没有显著的相关性,但是与比赛的最终成绩有显著的相关性,全程耗时最短的选手,往往是在比赛前后半程节奏保持一致、耗时非常接近的人。
对比男女选手之间的差异是非常有意思的事情,来看这两组选手前后半程差异系数的频次直方图:
sns.kdeplot(data.split_frac[data.gender=='M'], label='men', shade=True)
sns.kdeplot(data.split_frac[data.gender=='W'], label='women', shade=False)
plt.xlabel('split_frac')
plt.legend();
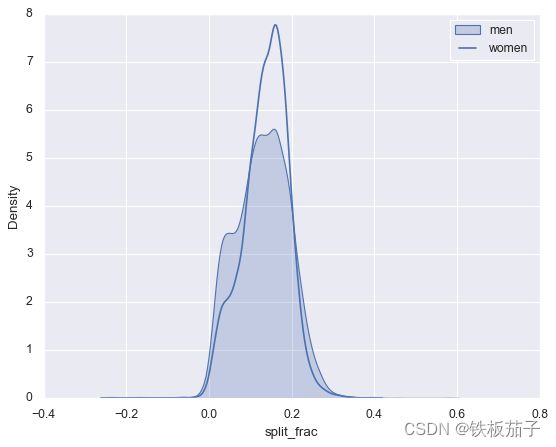
在前后半程耗时接近的选手中,男选手比女选手要多很多,男女选手看起来几乎都是双峰分布。我们将男女选手不同年龄的分布函数(用小提琴图)画出来:
sns.violinplot(x="gender", y="split_frac", data=data,
palette=["lightblue", "lightpink"]);
data['age_dec'] = data.age.map(lambda age: 10 * (age // 10))
data.head()
| age | gender | split | final | split_sec | final_sec | split_frac | age_dec | |
|---|---|---|---|---|---|---|---|---|
| 0 | 33 | M | 0 days 01:05:38 | 0 days 02:08:51 | 3938.0 | 7731.0 | -0.018756 | 30 |
| 1 | 32 | M | 0 days 01:06:26 | 0 days 02:09:28 | 3986.0 | 7768.0 | -0.026262 | 30 |
| 2 | 31 | M | 0 days 01:06:49 | 0 days 02:10:42 | 4009.0 | 7842.0 | -0.022443 | 30 |
| 3 | 38 | M | 0 days 01:06:16 | 0 days 02:13:45 | 3976.0 | 8025.0 | 0.009097 | 30 |
| 4 | 31 | M | 0 days 01:06:32 | 0 days 02:13:59 | 3992.0 | 8039.0 | 0.006842 | 30 |
men = (data.gender == 'M')
women = (data.gender == 'W')
with sns.axes_style(style=None):
sns.violinplot(x="age_dec", y="split_frac", hue="gender", data=data,
split=True, inner='quartile',
palette=["lightblue", "lightpink"]);
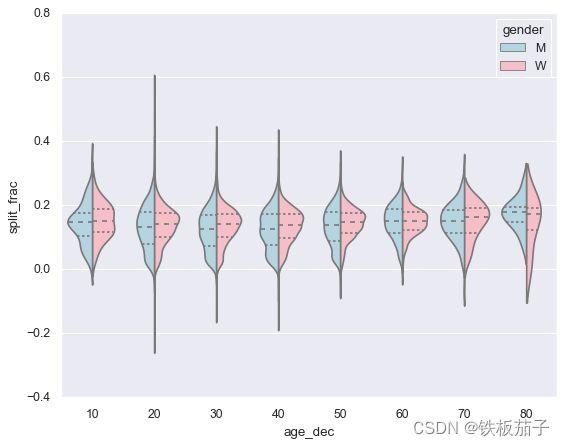
通过上图可以看出男女选手的分布差异:20多岁至50多岁各年龄段的男选手的前后半程差异系数概率密度都比同年龄段的女选手低一些。所有80岁以上的女选手都比男选手表现要好,可能是这个年龄段样本太少:
(data.age > 80).sum()
7
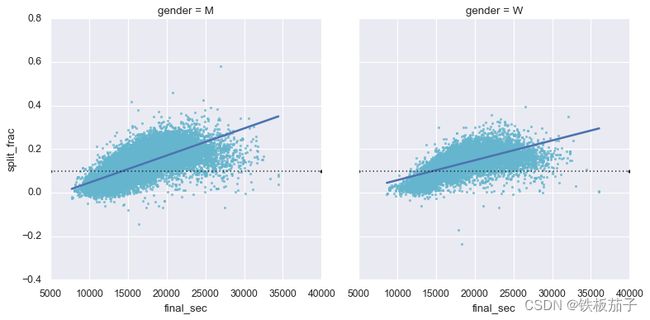
用regplot为后半程加速型选手数据自动拟合一个线性回归模型:
g = sns.lmplot(x='final_sec', y='split_frac', col='gender', data=data,
markers=".", scatter_kws=dict(color='c'))
g.map(plt.axhline, y=0.1, color="k", ls=":");
似乎有显著后半程加速的选手都是比赛成绩在 15000 秒,即四小时之内的种子选手。低于这个成绩的选手很少有显著的后半程加速。