算法笔记之进制转换（c++/c）

前言

学习了数据结构后知道进制转换可以用栈来操作。对于算法题目来说，我们可以用c++的STL库进行调用对应的数据结构类型。这里只是记录简单结构的算法思想，也就是模拟为主，后面有专门的STL库调用笔记，我会记录题目。

再细说进制转换。通常分为10进制转其他进制与其他进制转10进制。只要会这两种，遇到非10进制转换的，都是以十进制为中间过程的变化（也不绝对哈）。

这里如果对进制转换不太了解，可以看这个视频学习

进制转换视频学习

1. 其他进制转化为十进制

对于一个十进制数的计算如下

$$

12345=510^0+410^1+310^2+210^3+1*10^4

$$

对于二进制转化为十进制如下

$$

(1101)=12^0+02^1+12^2+12^3=1+0+4+8=13

$$

其他进制同理，我想不用过多说明，核心代码如下

题目链接：十进制转二进制

//二进制转十进制
//这里二进制数用的是字符串存储
int main(){
    int n,cnt=0;
    char a[50];
    scanf("%s",a);
    for(int i=0;a[i]!='\0';i++){
        int temp=a[i]-'0';
        //核心是该式不断乘2
        cnt=cnt*2+temp;
    }
    cout<

K进制转十进制

//k进制准十进制
int main(){
    char a[20];
    int sum=0,k;
    cin>>a>>k;
    for(int i=0;a[i]!='\0';i++){
        int t;
        //如果进制数大于9，就会出现字母来表示大于9的数字，这里只需要判断即可
        if(a[i]>='A' && a[i]<='F'){
            t=a[i]-'A'+10;
        }else{
            t=a[i]-'0';
        }
        sum=sum*k+t;
    }
    cout<

2. 十进制转化为K进制

算法思想：模拟+除基取余法；就是利用循环来实现除基取余法的操作，也是中国部分适合使用栈来存储余数，不过这个也是后话了

除基取余法

核心：不断除以K，余数由高到低排列得K进制数

十进制数值较小时的简单转换（模拟）

两者本质差不多，只是在字母处理上有所增加

十进制转二进制

题目链接

#include
using namespace std;

//10进制转2进制
int main(){
    int n,a[20],cnt=0;
    cin>>n;
    //核心代码，不断取余并且存放到数组里面
    do{
        a[cnt++]=n%2;
        n/=2;
    }while(n!=0);
    
    //输出时反向输出即可
    for(int i=cnt-1;i>=0;i--){
        cout<

十进制转K进制

题目链接

#include
using namespace std;

//十进制转k进制
int main(){
    int n,k,num=0;
    cin>>n>>k;
    //除基取余法求k进制
    //和前面的二进制不太一样，这里余数超过10的用字母表示
    char a[50];
    do{
        if(n%k<10)
            a[num++]=n%k+'0';
        else
            a[num++]=n%k-10+'A';		//这里注意减10
        n/=k;
    }while(n!=0);
    for(int i=num-1;i>=0;i--){
        cout<

大数模拟型十进制转二进制

题目链接

算法思想：

为什么说是大数转换呢？int 范围是10^9以内（2的31次方-1），long long 类型范围是10^18次方以内（2的63次方-1），显然输入的非负整数为30位，是可以超过long long 类型范围，所以只能用数组存储；

但是数组存储该数，如何取余？

这道题的难点就是这里，希望你可以对数组来进行模拟除基取余法

除法是从最高位开始，不断右移到个位。除数为小于十的数字，就直接一位一位的比。当当前数字有余数时，则余数*10再加上下一位接着除。

==数组除以2的代码，注意要用x来记录前面一位的余数==

//对该大数进行除以2的处理
//x表示前一位除以2余留下来的数
//tmp存储该位数除以2之前的数字
int x=0,tmp;
//p是最高位，这里p是会不断右移的
for(int j=p;j

==当然除了要除以2，还要不断存放余数，直到该数组全部为0==

//余数由末尾奇偶得
ans[i++]=str[len-1]%2;

//注意之前的记录最高位的p也要判断再右移
if(num[p]==0)	p++;

具体代码实现

//solution1：模拟除基取余，但是对于字符串的处理很特殊
//对于末尾奇数，取余为1，偶数就是0
//对于整个字符串除以2，从最高位开始除，如果有余数，用x代替留到下一位来除
//循环截止的条件是到最低位为0
int main(){
    char str[50];
    int num[50],ans[1005];
    while(scanf("%s",str)!=EOF){
        //问题来了，这个大于ll 量的整数如何取余？
        //对于整个数组计算？

        //先将字符转化为整数
        for(int i=0;i=0;m--){
            cout<

当然这里也有一个用c++STL库操作的，先写在这里做参考

#include
#include
using namespace std;
//字符串的除法函数
string divide(string s,int x){
    int remainder=0;
    for(int i=0;i>s){
        vector bi;
        while(s.size()!=0){
            int last=s[s.size()-1]-'0';
            bi.push_back(last%2);
            s=divide(s,2);         
        }
        for(int i=bi.size()-1;i>=0;i--){
            cout<

3. 其他进制之间转化

思想很简单，以十进制为之间过程，然后用上面的方法进行转换

题目链接

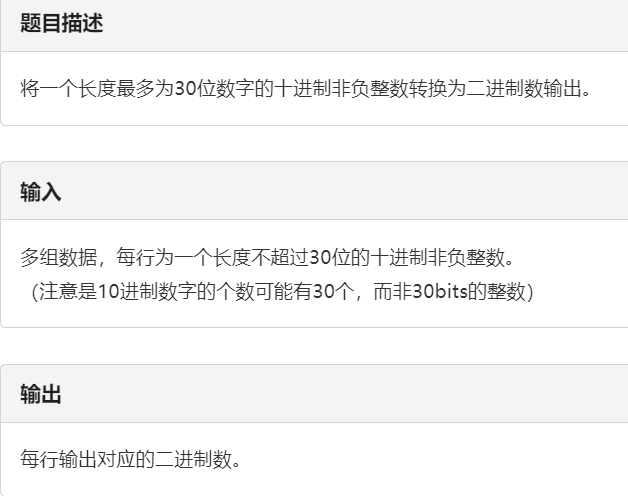
题目描述
求任意两个不同进制非负整数的转换（2进制～16进制），所给整数在long所能表达的范围之内。不同进制的表示符号为（0，1，...，9，a，b，...，f）或者（0，1，...，9，A，B，...，F）。
输入
输入只有一行，包含三个整数a，n，b。a表示其后的n 是a进制整数，b表示欲将a进制整数n转换成b进制整数。a，b是十进制整数，2 =< a，b <= 16。
输出
可能有多组测试数据，对于每组数据，输出包含一行，该行有一个整数为转换后的b进制数。输出时字母符号全部用大写表示，即（0，1，...，9，A，B，...，F）。

#include
typedeflonglongll;
usingnamespacestd;
​
​
//数制转换
intmain(){
    inta,b;
    charn[100];
    while(scanf("%d %s %d",&a,n,&b)!=EOF){
        //cin>>a>>n>>b;
​
        //将n转化为10进制
        llsum=0;
        for(inti=0;n[i]!='\0';i++){
            inttemp;
            if(n[i]>='0'&&n[i]<='9')  temp=n[i]-'0';
            elseif(n[i]>='a'&&n[i]<='f')     temp=n[i]-'a'+10;
            else    temp=n[i]-'A'+10;
            sum=sum*a+temp;
        }
​
        //10进制转化b进制
        chart[100];
        intnum=0;
        do{
            if(sum%b<=9)
                t[num++]=sum%b+'0';
            else
                t[num++]=sum%b-10+'A';
            sum/=b;
        }while(sum!=0);
​
        for(inti=num-1;i>=0;i--){
            cout<