1000以内的正整数中的所有素数

     以下内容和代码主要参考了这位兄台和这位兄台的。
     素数又称为质数，它是在大于1的自然数中只能被1和其自己整除的数。
     那么判断素数最简单的方法是看其是否只能被1和其自己整除的数，如果是则它是素数，否则不是。看如下源代码。

bool isPrime(int n)
{
	if (n < 2)
	{
		return false;
	}
	for (int i = 2; i < n; i++)
	{
		if (n % i == 0)
			return false;
	}

	return true;
}
int main()
{
	bool prime[1001] = { false };
	for (int i=2;i<1001;i++)
	{
		if (isPrime(i))
		{
			cout << i << " is prime\n";
			prime[i] = true;
		}
	}
}

     如果一个大于1的整数n可以被1和n之外的另一个整数$k_1$整除，则有$n=k_1\ast k_2$且$1<k_1<=\sqrt{n},\sqrt{n}=<k_2<n$或者$1<k_2<=\sqrt{n},\sqrt{n}=<k_1<n$。因此当我们通过验证一个大于1的整数n是否只能被1和其自己整除的方法来验证其是否为素数时可以只迭代到$\sqrt{n}$而不用迭代到$n-1$。代码如下所示。

bool isPrime(int n)
{
	if (n < 2)
	{
		return false;
	}
	//for (int i = 2; i * i < n; i++)
	for (int i = 2; i < sqrt(n); i++)
	{
		if (n % i == 0)
			return false;
	}
	return true;
}
int main()
{
	bool prime[1001] = { false };
	for (int i=2;i<1001;i++)
	{
		if (isPrime(i))
		{
			cout << i << " is prime\n";
			prime[i] = true;
		}
	}
}

     素数从2开始，2是素数则$2\times 2,2\times 3,2\times 4,...$都不是素数，因此可用排除法来求得所需的素数。代码如下所示。

int main()
{
	bool prime[1001] = { true };
	for (int i = 0; i < 1001; i++)
	{
		prime[i] =  true ;
	}
	for (int i=2;i<1001;i++)
	{
		if (prime[i])//如果i为素数则i的倍数都不为素数
		{
			for (int j = 2 * i; j < 1001; j += i)
			{
				prime[j] = false;
			}

		}
	}

	for (int i = 2; i < 1001; i++)
	{
		if (prime[i])
		{
			cout << i << " is prime\n";
		}
	}
	return 0;
}

     以上的算法中，2是素数则$2\times 2,2\times 3,2\times 4,...$都被我们排除了，但是i迭代到3时$3\times 2$即$2\times 3$又被重复的排除了一次，这是多余的。因此每次迭代到i时可以从$i\times i$开始排除。以下是代码。

int main()
{
	bool prime[1001] = { true };
	for (int i = 0; i < 1001; i++)
	{
		prime[i] =  true ;
	}
	for (int i=2;i<1001;i++)
	{
		if (prime[i])//如果i为素数则i的倍数都不为素数
		{
			for (int j = i * i; j < 1001; j += i) //从i的平方开始排除
			{
				prime[j] = false;
			}

		}
	}

	for (int i = 2; i < 1001; i++)
	{
		if (prime[i])
		{
			cout << i << " is prime\n";
		}
	}
	return 0;
}

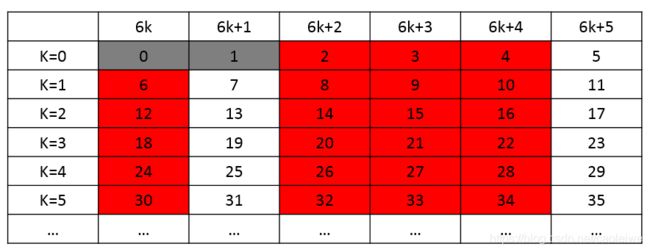
     如果$k>=1$，对于$6k,6k+1,6k+2,6k+3,6k+4,6k+5$，按照素数的定义$6k=3\times (2k),6k+2=2\times (3k+1),6k+3=3\times (2k+1),6k+4=2\times (3k+2)$绝对不是素数。$6k+1，6k+5$有可能是素数。对于$n,n>=6$如果它对6取模后不等于1或者5，则它肯定不是素数，如果它对6取模后等于1或者5可以再另行检查。又因为$6k+1，6k+5$为奇数且$6k+1=3\times (2k)+1，6k+5=3\times (2k+1)+2$，所以它们肯定不能被偶数整除且肯定不能被3整除。从前面的算法我们可以知道判断一个数n是不是素数，只需判断其能否被2到$\sqrt{n}$的数整除，通过以上的讨论以及图1现在只需判断其能否被在范围$2->\sqrt{n}$内且且不在红色区域内的数整除来判断其是否是素数。可以得到如下代码所示的算法。

　 图1.

int main()
{
	bool prime[1001];
	for (int i = 0; i < 1001; i++)
	{
		prime[i] =  true ;
	}
	prime[0] = false;
	prime[1] = false;
	prime[4] = false;

	for (int i=6;i<1001;i++)
	{
		if ((i % 6 != 1) && (i % 6 != 5))
		{
			prime[i] = false;
			continue;
		}
		else
		{
			for (int j = 5; j <= sqrt(i); j += 6)
			{
				if (i % j == 0 || i % (j + 2) == 0)
				{
					prime[i] = false;
					continue;
				}
			}
		}
	}

	for (int i = 2; i < 1001; i++)
	{
		if (prime[i])
		{
			cout << i << " is prime\n";
		}
	}
	return 0;
}