路径规划-learning

参考视频：【全】无人驾驶系列知识入门到提高

本文旨在对视频内容规划控制方面做一些学习记录，希望帮助有需要的人学习提高。不对处，望指正。

---

文章概要：
1 什么是规划
规划的本质、如何解决规划问题
2 传统的规划方法
机器人学基础、经典算法
3 无人车的规划
Routing、Planning、Lattice Planner
4 Apollo如何求解规划问题
EM planner DP、QP求解

1. What is motion planning?

规划planning目前是无人车最困难也最有挑战的部分

1.1 本质：

1. 求解：$argmi{n}_{x}f(x)$
   获取$f(x)$最小值就是规划;$f$可以理解为成本，$x$可理解为轨迹，追求最小成本就是规划的本质。
2. 规划问题也可理解为搜索问题
   –【比如】Google：Quary词，返回最优结果
   –无人车：当前环境和当前状态，返回当前路径上的最优选择
3. 定义一个好的规划（取决于目标函数）
   $f(x)$的最优解

运动规划 motion planning 的三个领域

1. 机器人领域robot fileds：
   规划领域理解：生成轨迹，实现目标
   经典的实现算法：RRT、A*、D*、D* Lite
2. 控制领域control theory:
   规划领域理解：动态系统理论，实现目标状态（从而完成planning）
   经典的实现算法：MPC、LQR
3. AI：生成状态和Action的一个映射
   实现方法：Reinforcement learing(强化学习),Imitation learing(模仿学习)

1.2 如何解决一个规划问题motion planning

1 突破口：规划问题简化成一个简单问题：path finding problem

不关心速度、不关心走，周围环境固定

2 简化后的问题转变为：路径选择问题
算法演示网址：http://qiao.github.io/PathFinding.js/visual/
最好的path是怎么样的?路径最短的path
DFS、BFS方法查找最短路径有缺陷的，假设地图无限大，就有可能无法搜索到目标点，也就是说有可能无法找到路径
–A* search：基于Dijkstra的改进算法。

【不离散化，对连续空间的求解比较困难，这是因为连续空间求解会涉及解析式，该式求解比较困难；所以，离散化网格处理是机器人通用的路径求解方式之一。高效的离散化，高效的网格化，是研究的重点】【A算法，面试时候，公司都会要求至少写出一个A思路】

3 无人车的规划和A* Search相差多远

1、无人车属于部分感知
2、无人车周边的障碍物属于动态的，而且该障碍物不确定性极高。
3、无人车的环境比较复杂，例如有交通规则、碰瓷

上面展示的A*算法，是知道了全局、周边环境以及终点位置，而无人车只是局部信息，也不知道终点具体在哪

4 A* 本身是一个Global Algorithm（百度地图）

• global Routing
  将rounting路由信息传给无人车，从而进行一个细节的规划

5 部分感知情况解决方式
贪心算法：增量式搜索：把目前获取的状态信息，求解出最优解

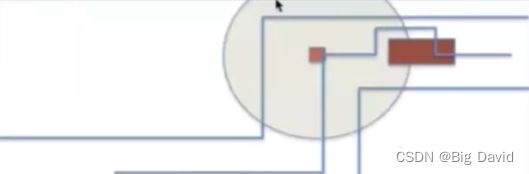
D* 算法（A* 进行改进）：对部分环境信息的一种search，典型运用是，Apollo登月小车；后面，D* 算法发展成更轻量级算法D* lite(D* lite算法，利用当前信息对全局信息进行一个修正)。

6 求解全局最优
难度不小，不一定要全局最优。
部分最优从而接近全局最优的理论

7 informative &non-informative search【有提供信息与无提供信息的搜索】，两种感知方式：Global & partial observed【全局与局部方式】
无人车： partial observed & informative search

8 至此，解决无人车搜索问题，可以尝试有如下方法：
（1）首先定义一个目标函数，目标函数并且结合了平滑性和目标cost
（2）使用通用的Search方法来最小化cost，从而找到一个最优解
（3）通过partial observed information 来做局部planning

9 对于无人车规划而言，还缺少一些东西
（1）处理动态障碍物，动态环境（如果将动态环境也作为静态处理，会导致很大问题）
（2）处理交通规则（涉及公共安全问题）
（3）实时计算（无人车要求的planing是在100ms-150ms之间；人的反应时间一般在300ms-500ms，酒驾时会达到1000ms）：就是在有限时间内找到最优解。也是无人车开发，一般使用C++，而不是使用python，由于C++算法有更多的实时性优化。

10 无人车motion planning的定义
（1）safely安全性
（2）smoothly平滑性，保证乘客舒适性（体感）
（3）Achieve to destination到达目的地
（4）X，Y，Time:3D trajectory optimization problem（规划问题，也可视为三维轨迹优化问题）
（5）无人车硬件信息：定位设备、感知设备
（6）无人车软件信息：动态信息（感知、预测、定位）、静态信息（HD MAP：实时性的保证。如果静态信息不是使用HD MAP提供的，而是通过感知获取的，那么实时性大大降低）
（7）设计出一个合理的轨迹：路径path（运动路线设计）、速度speed（到达目的地速度设计）

2 传统的规划方法

2.1 基本planning方法

1 经典基于环境建模的方法
(1) RRT
(2) Lattice

2 现代无人车planning方法
(1) Darpa 无人车开发的方法
(2) Lattice in Frenet Frame (这里的Lattice和上面的是有区别的)
(3) Spiral polynomial 解决无人车平滑性所采用的一种思路

来自：A Review of Motion Planning Techniques for Automated Vehicles

3 质点模型
(1) 将物体看成一个质点(A*,BFS)
(2) 点与点不碰撞

4 刚体问题(无人车可视为一个刚体)
(1) BycicleModel 自行车(单车)模型 ：无人车建模的一种基本方式
(2) XY Heading : 有方向的X、Y，可理解为矢量
(3) Collision: 碰撞条件比点与点的更严格；而且，碰撞检测更复杂

5 Planning限制条件
（1）避免碰撞
（2）边界阈值：理论人和车距离3-8米，但是由于车的传感器并没有人的感觉器官反应能力那么优秀，由于传感器数据传输有延迟这些，为了避免安全事故，车与人的距离应该更远，这个安全距离可视为阈值

6 连续空间问题解决方式
（1）离散化
（2）网格化

2.2 传统的机器人基础

1 PRM（Probabilistic RoadMap Planning）【非常实用的一个方法】

开始点s,目标点g，由于连续空间中计算能力比较弱，而且也不知道全局环境，所以该方法采用撒点方式，如图中紫色点，如果撒点和障碍物重合了，就把该点去掉；洒的点多了，自然可运行空间就出来了；但是撒的点不会过多，这是因为只是为了达到目标点g,而不是走每一个角落。

（1）连续空间离散化：1.随机撒点【全空间撒点】2.【撒在】Obstacle上的点就删除
（2）连接可行点，形成可行空间
（3）A*【获取运动轨迹】

2 RRT（incremental version of PRM：上面的PRM方法的改进版本）

增量式解析：图中点T想在空白区域行走，先撒两个点
（1）使用增量搜索方式进行
（2）找附近可行点的最优点：1.f(x)最小，成本cost最小 2.走过程不能有阻碍，如路面不平，尽量使得这个cost小
（3）运动过程中，还有可能碰到障碍物

（4）撒点搜索距离不能太远（上图就是撒点太远，导致碰到障碍物）
撒点需要一步一步移动

这里撒点移动路线属于折线，对于质点移动还行；但是对于刚体移动来说，属于曲率无穷大，是不行的；
此外，这种撒点方式还不能解决动态障碍物问题

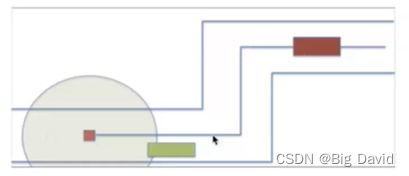
3 Lattice方法

（1）改进了RRT的折线问题
（2）目的是给出path的平滑曲线
（3）采用的思路是，网格化（将搜索空间替换成一个一个小格子；每个采样格都是用曲线连接。如上左图中每个网格内，连接曲线都是平滑的）
（4）该方法属于指数级别的搜索算法（NP-Hard）：是该算法的一个缺点

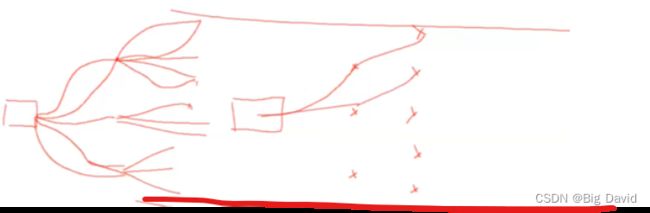
指数级别的理解：一开始无人车所处的点有5根曲线，当达预测到下一个点时候，每个预测点又有多根曲线，这就是指数级别的增长了。
改进该缺点：改进了曲线搜索方式。
比如，第二级中的曲线到达的点相隔很近，那么，没有必要再取这么多点的，把相近的点合并一个处理，加上撒点范围的约束（道路两侧约束），就可以避免了指数级的搜索空间增长。最后，形成一种点线连接的搜索方式。
后面采用的点线搜索方式降维，这是由于使用了动态规划

4 DP 动态规划
(1)减少了搜索空间：通过复用已有结果(搜索过的路径空间保存下来)
(2)Lattice DP曲线的平滑度情况: 曲率连续、曲率导数不一定连续(联系到无人车,曲率不连续,有可能出现上一瞬间打方向盘90°，下一瞬间打180°，明显不符合驾驶习惯的)

5 QP 二次规划
解决4里面Lattice DP曲线曲率导数不连续情况。
（1）凸优化问题最优化求解
（2）公式表达：
$$\begin{gathered} minimize\frac{1}{2}{x}^{T}QX+c^{T}X \\ subject:Ex=d,Fx\le m \end{gathered}$$
（3）QP如何找到平滑曲线
性质：在凸优化中的凸空间问题，用QP有最优解
$$\begin{gathered} min|f^{\prime }{|}^2 \\ min|f^{\prime \prime }{|}^2 \\ min|f^{\prime \prime \prime }{|}^2 \end{gathered}$$
对应的导数都是最优的，此时可以保证平滑曲线存在。
用高维导数的连续来保证平滑
其他的平滑曲线方法：贝塞尔曲线（多阶多项式都平滑，从而保证曲线平滑）、样条插值方法

6 刚体模型

建模时候，后轮轴线中点设置为车的原点（0，0）。前轮轴中心设置为前轮中心的拐点。
1 前轮转向和Heading的关系
（1）车轮是沿着切线方向行驶
（2）前后轮是同一个旋转中心
（3）左右轮的结构相同（排除差速情况）：假设前后轮绕转同一个中心旋转，那么会是一个环形状，由于前后轮旋转半径不一致导致的

2 Bicycle Model

将左右轮简化，以中轴轴线为中心建立车轮关系，得到上图的单车模型；w表示的是前轮转角
曲率公式：$kappa=\frac{1}{R}=\frac{tan(w)}{L}$

3 无人车的规划

无人车planning定义：A点到B点，构建一个车辆运动轨迹，结合 HD MAP，Localization和Prediction
输入：结合模块的信息
输出：可行性轨迹，有一系列点组成（点使用X，Y，time来表示）
tip:注意要轨迹要避免碰撞，体感舒适

两个层面：

• 导航层面：获取开始点到终点的基本路线；可视为一个粗略的planning
• 运动轨迹层面：给出在路线前进时，运动的细节轨迹；可视为一个细节的或者多层面的planning

3.1 Routing

Routing定义：导航一条从A到B的全局路径
1 输入：地图（路网信息、交通状态）、当前位置、目的地（乘客决定）
2 输出：可行驶道路的连接线
3 搜索：地图数据（高精地图）转化成图网络

节点表示道路：node的划分可以自定义的，并不是一条道就是node，比如靠左靠右划分两个node也是可以的
边表示道路连接：里面道路权重是不一样的，左右转不一样，拥堵情况也会影响权重,左转的cost比较高原因是，其碰撞风险更高，左转还需要等红绿灯。

4 经典算法A*
最经典的路径查找算法
$F(n)=G(n)+H(n)$
F(n)表示道路的routing的总cost;G(n)表示起始点到候选点的cost;H(n)表示候选点通过启发函数得到的目标点cost

A算法的重点:启发函数怎么得到

每个格子，中间值就是F值，上两个值就是G和H的值，亮橙色为起始点，启发式搜索一圈，也就是围绕这个点搜索一圈每格子的总cost，发现是其下面的cost40为最小，则移动到下面的格子，循环往复达到绿色格子上。

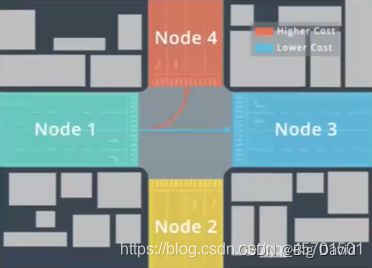
5 真实地图中的应用

左转cost最大，结合上图来看，红色表示左转，蓝绿色表示直行，淡蓝色表示右转。

比对发现，右转的总cost最小，那么选择右转：导航地图路线搜索的基本思路。

（1）planning可理解为高精度、低级别的一个search，称为trajectory planning（轨迹生成，轨迹由点组成，该点带有相对当前的时间以及速度；提供速度的目的是，为了方便后面做跟踪）

（2）轨迹点：X、Y、time、Velocity（道路坐标系中的坐标XY、相对当前的时间、速度）
实际情况，速度是存在抖动情况的，也就是速度平滑性不能保证的，所以不能简单利用轨迹点和时间来求取速度；这里使用了速度信息，然后让control来跟踪。并不是一定是给定速度，而是，给出速度，可以更好让后续模块跟踪轨迹点

（3）规划的约束条件
1.Collision 碰撞：躲避任何障碍物
2.Comfortable 舒适性：路径点必须相对平滑、速度也要平滑
3.运动学约束：高速转弯（有侧翻可能）、掉头曲率角度
4.illegal 合法：符合交通法规、符合人类约定俗成规则

（4）cost function成本函数

• 真实情况下有多条可行轨迹
  

• cost由许多条件组成
  1.道路偏移中心线距离（越偏离，cost越大）
  2.碰撞或者靠得太近（对应cost越大）
  3.速度太快，超速（对应cost越大）
  4.curvature曲率太大，打方向盘太急（对应cost越大）

• 不同场景下我们可能有多个不同的cost function
  1.高速场景（速度慢是一个大cost）
  2.停车场（速度慢是一个小cost）
  3.不同车辆（卡车和私家车的cost不一样）

（5）Frenet坐标系（车道坐标系）

笛卡尔坐标系（世界坐标系）
局限：
1.xy坐标无法知道无人车开了多远
2.不知道有没有偏离中心线
3.也不知道道路在哪

更好的坐标系：Frenet

注意和Track坐标系的区别：
1.L方向不同（朝右）
2.Track是基于Road级别
3.Frenet是基于Lane级别

S表示走了多远,L表示距离车道有多偏。

（6）Path VS Speed 解耦
轨迹生成和速度生成需要解耦；只有解耦，才能使得每个部分的形成凸问题，只有凸问题才能使用QP来处理；当混合一起，就不是凸问题，求解空间会非常丰富

Path planning：
生成可行轨迹路径
Cost:1.path平滑性2.安全性3.道路中心偏移距离
选择出成本最低的一个path planning

speed planning:
每个path上选择一系列速度（每个点都有速度），生成速度轨迹

（7）Path Planning

1.首先生成道路网格（GridMap网格地图）
2.每个网格单元中随机采样（撒点）
3.每个网格选一个点
4.组成多条候选path

Cost Function对这些轨迹进行评估，需要考虑：
1.找到一个成本最低的一个
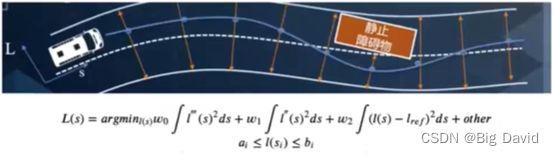
2.中心线距离 $l\ast a_0$
3.障碍物距离$d\ast a_1$
4.速度变化率$acc\ast a_2$
5.曲率$kappa\ast a_3$ 为什么是kappa？舒适性原因。如果曲率不平滑，必然会有打方向盘很急，乘客难受，也有翻车可能性。
$F(x)=l\ast a_0+d\ast a_1+acc\ast a_2+kappa\ast a_3+a_4$
cost线性加权，如果在参数可调情况下，就可以达到局部最优

（8）Speed planning
ST图

ST图中的S并不是指道路S，而是指给定path的S
ST图将三维XY、time空间，降维到ST的二维空间，其中path锁定了XY，这里理解图中的S，这样可以使得无人车规划求解过程中，有了数学工具，如QP，进行求解。
S表示Path上纵向距离，T表示运动时间

（9）如何规划ST轨迹

1.连续空间离散化（grid map网格地图）
2.每个单元格速度保持不变（每个单元格的速度线，在图中不能是曲线连接，只能使用折线连接）
3.把障碍物投影进来（投影到ST图）

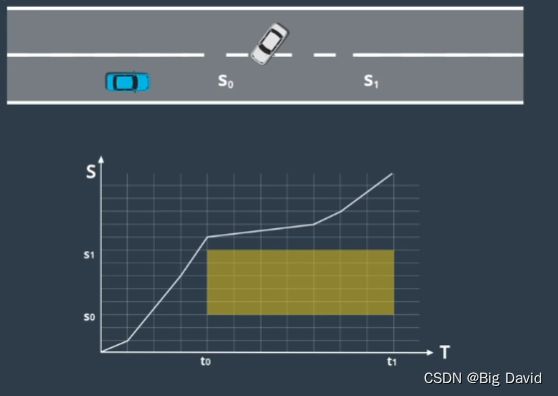
挡住给定的path轨迹的部分画进ST图中，因此必须要有良好的预测轨迹。t0，t1时刻障碍物会在我们的path轨迹中挡柱s0,s1部分。
4.速度曲线不能碰撞这个区域

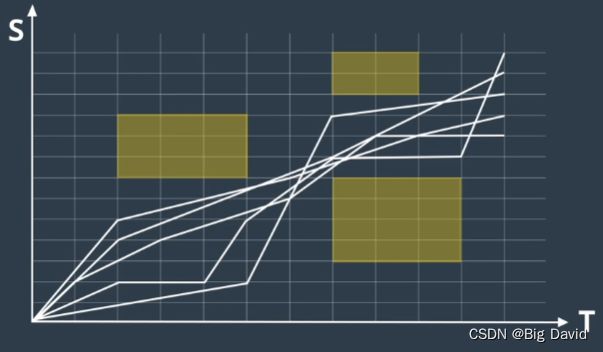
5.凸优化求解得到最优的速度曲线

search搜索
----限制条件：速度限制、距离限制（安全距离）、车辆动力学限制（车的加速度、刹车性能）

（10）如何优化？折线不平滑，需要优化

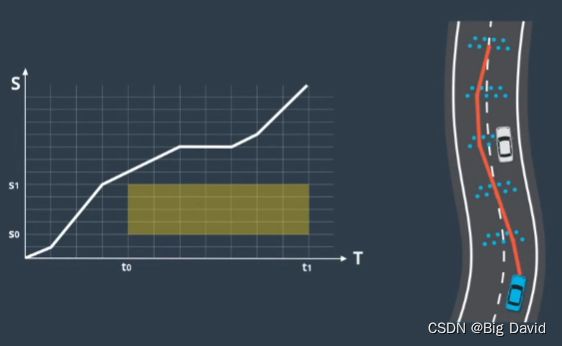
1.对不平滑的速度线进行优化
使用QP（二次规划）进行优化：通过QP约束速度，约束加速度，约束加速度导数，使得平滑非线性曲线和平滑的加速度曲线，达到一个拟合程度；拟合程度多少，由QP约束条件来确定
2.这个方法很大程度依赖于连续空间离散化
3.网格、单元格方法
不平滑，解决：Quadratic Programming 二次规划、将平滑的非线性曲线与这些线段进行拟合、有现成工具qpOASES

（11）轨迹规划
遇到一辆很慢的车，如何超车

1 生成很多轨迹线（撒点采样）

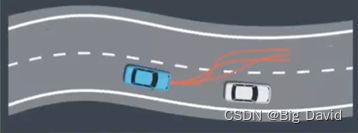
2 cost function对其进行评估，选择cost最小的一条（比如安全距离太小导致cost过大，直接去掉）
3 生成一个ST图表述速度规划
4 生成多条速度曲线（撒点）

5 使用优化工具对多条速度采样进行最优化求解（cost成本函数，constraints约束）：优化，就是保证每个点的加速度最小，加速度平方最小，加速度导数平方也最小
让整个路线和速度曲线变得平滑

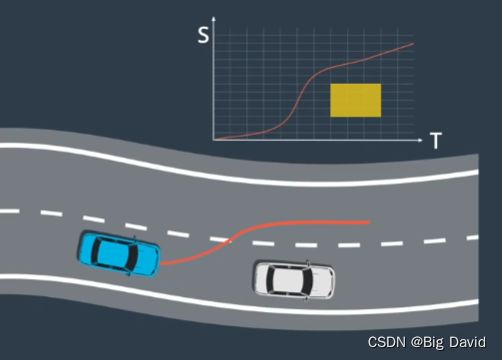
6 最后将每个轨迹点（跟自定义的轨迹点resolution）的path、speed合并得到最终结果

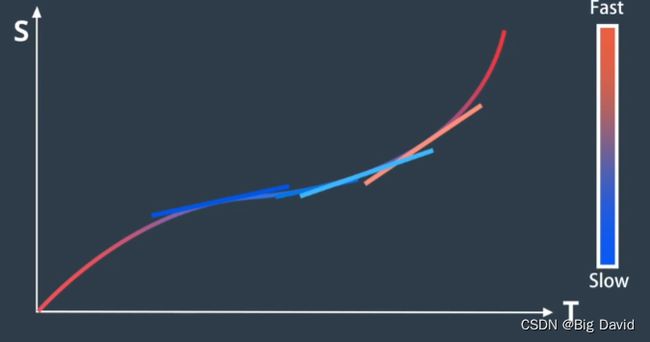
红色表示速度较大，青蓝色表示速度低
规划思路是，path和speed是分开规划。

3.2 Lattice planner

规划思路是，path和speed合并一起规划
1 SL轨迹和ST轨迹


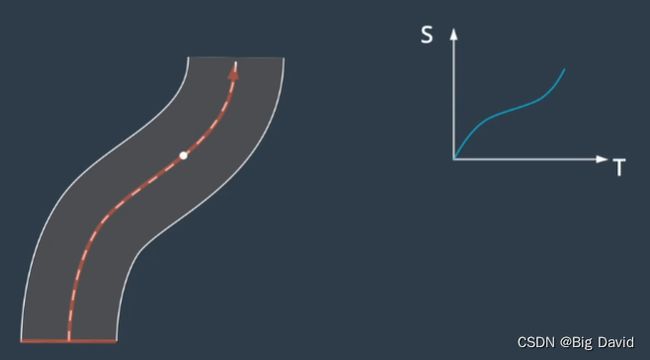
2 Lattice将两个图合并处理，同时进行path和speed的采样
3 实例：一个切车场景

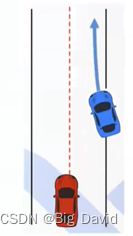
1.先对整个候选轨迹进行采样

红色线表示红车的预测轨迹范围，短的表示速度慢，轨迹分布情况，长的表示速度快，轨迹分布情况
2.设计一个合理的cost
3.选择一个cost最小的轨迹
4.条件检查和碰撞检查

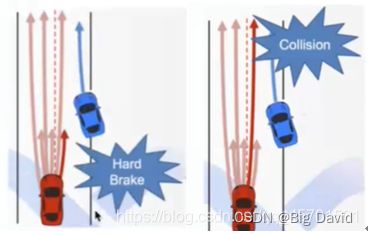
左侧路线有急刹情况；右侧有碰撞情况
5.检查失败，则返回继续找cost次优选项

6.成功输出结果

Lattice因为其采样计算量大，为了优化其采样效果，需要先进行场景化以简化计算量:Lattice的一个弊端，计算量很大，如果预测5s到8秒时，计算量指数爆炸增长。

4 分场景使用Lattice：Cruising，Following and Stopping：对S方向进行优化【特定场景使用lattice】
lattice这种规划方式在2006年时候使用后，因为计算量大而逐渐退出无人车领域；但是在物流小车比较适用，由于物流小车的速度没有那么快，采样量比较小，这种比较适合lattice

下面三种场景，减少了lattice的采样点，从而减低计算量
1.Cruising：定速行驶
v=vc，a=0
这种状态，不需要采样
2.Following：跟车行驶

• 需要对s和t同时采样
• 规定时间t跟在某个车的后面【减低可选点范围】
• 保证安全距离
• 速度$v=v_1$
• 加速度$a=a_1$

3.Stopping：停止

• 对车辆在哪里停下来进行采样
• s和t同时采样
• 加速度a=0
• 速度v=0

5 Lattice对L方向进行优化
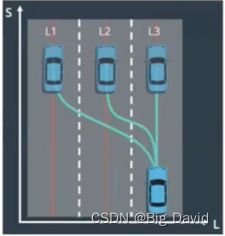需要保证车辆以一个稳定的状态进行终点状态，比如与本车道线平齐
$H^{\prime }=0,H^{\prime \prime }=0$:横向的 速度、加速度都为0(这是lattice对L方向优化)
$S’=0,S’’=0$纵向的 速度、加速度都为0

6 合并ST和SL坐标
1.转化到Cartesian坐标系
2.生成X Y time 三维轨迹
3.两个坐标系都有S；找同一个S对应的L和T

ST曲线也是先简化为凸函数

凸问题感性认识：以前面有车掉头为例，无人车有两种情况，一种是加速赶在掉头车前通过，另外一种情况，等待掉头完毕再通过，这时候求解path规划不是凸问题；假设，我们告诉无人车只能超速通过，这时候，path规划求解就是一个凸问题求解

3.3 上述两种无人车规划方式小结

1. path和speed分开规划【两者交替进行】
2. path和speed合并规划【lattice方式】
3. 二次规划，主要是对非平滑曲线进行平滑处理；二次规划QP可以处理任何凸优化问题。超车时，如果最优的cost还是很大，系统会不进行超车操作，这是决策层决定方案的执行与否的；也就是说，方案的cost出来了，最后是否实施，是由决策层决定的；并不是最优了就一定会执行

4 Apollo求解规划问题

Apollo采用了上述两种方式，但主要是以交替方式为主

4.1 Constrains约束

1.soft contraints&hard constraints（软、硬约束）
2.
3.constraints：
（1）交通规则：Hard constraints
（2）用QP或者Hard code 方式精细处理（这些约束，都会放到二次规划QP求解过程中）
4.Decision
（1）决策：soft constraints
（2）用DP的方式来处理一些人为设置的软约束（例如不往障碍物右侧撒点，就不会往右边走了）
5.最优轨迹
通过二次规划QP生成最优轨迹

4.2 如何换道

1.无人车想要换道怎么办

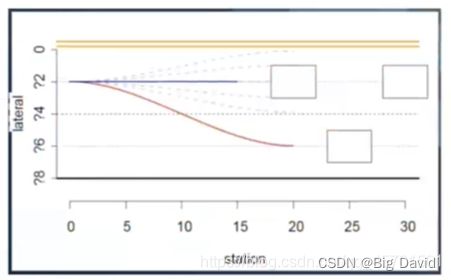
2.换道考虑很多安全性问题
-给出两种轨迹结果，让后续模块判断【一种换道轨迹，一种不换道轨迹】
3.Reference Line Decider
(1)判断换道时，是否安全
(2)拿到信息比planning丰富【例如，观测后方是否有来车，目的保证安全】
(3)做很多准备工作【例如决定换道时，提供打方灯的指令】

4.3 EM Planner（Apollo）

1.EM，期待最大化

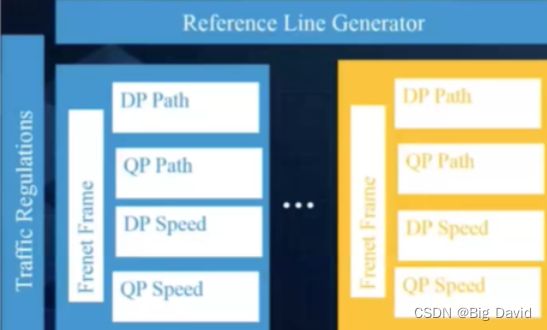
EM思路，单个维度求解最优解，然后叠加所有维度的最优解，得到的最优解（和一开始使用多维度计算最优解得到结果差不多）

2.上图基本流程：
（1）首先生成一条Optimal Path（理想path）
（2）再生成一条当前（理想）path情况下的optimal speed
（3）再将目前的speed返回给path进行一次tuning
（4）将tuning的path返回给speed做优化
（5）最后迭代到最优解
（6）贪心算法：Local Optimum
3.Apollo规划基本框架图

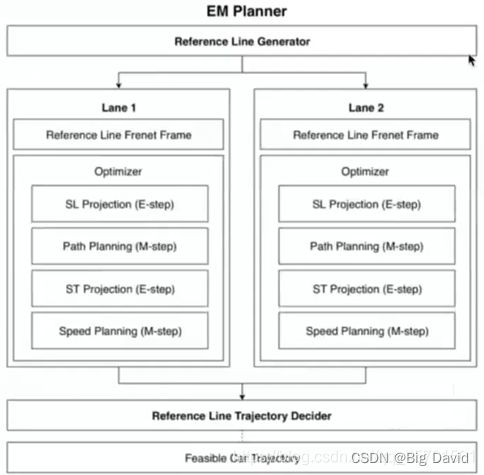
4.框架总结：
（1）三个关键步骤：
目标函数：线性加权的cost
限制条件：交通规则、碰撞条件（无穷大）、动态特性（车辆能力）
优化求解：如何计算最优解（DP+QP）

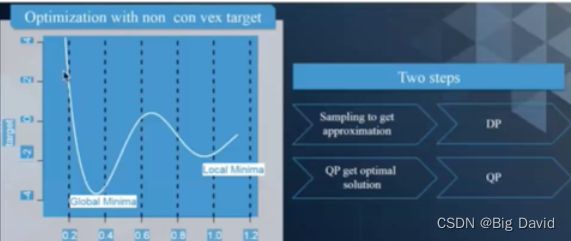
DP：不要求问题是凸的；QP：是一种凸优化
（2）DP、QP求解

1. path QP：

问题抽象：根据当前驾驶信息和道路状况建立平滑的SL坐标轨迹
模型建立：合理优化目标函数和约束条件
优化方法：二次优化求解带约束的二次规划问题

2. speed DP

问题抽象：使用ST图
模型建立：cost函数（障碍物、曲率、无人车状态）
优化方法DP最优求解

s’=v 速度
s’’=acc 加速度
s’’’=jerk 踩油门或刹车的速度

3. 计算提速思路

(1)SL坐标系离散化处理:粗分辨率使用时机、细分辨率使用时机(障碍物复杂，分辨率低一些；不复杂时分辨率则大一些)
(2)GPU并行计算:同时计算多条reference lane(参考路线)的结果
(3)QP Hotstart:1.QP的性质(QP的原理是泰勒展开)2.两帧之间差距不大(上一帧结果启发下一帧开始也是可以的)
(4)精通C++:利用编码思路来提升处理速度

5 总结

• 规划的定义：规划本质就是一个搜索过程。
• 机器人学的基本规划思路：PRM(撒点)->RRT(增量式撒点)->lattice（平滑折线）->动态规划DP（降维）->二次规划QP（平滑曲线）
• 无人车规划特点：先用path求解，再用speed规划【path和speed交替求解】；path和speed结合求解
• Apollo中EM Planner：path、speed规划中，添加了EM（期待最大化）思想，求解当前维度下的最优，循环迭代找到更优的结果，这样子防止出现局部最优的带来的限制。目的获取全局最优结果

1）预测模块在规划的作用体现就是，使得障碍物可以被绘制到ST图中
2）轨迹规划流程：网格化、撒点、利用搜索找到折线轨迹，再利用QP进行平滑处理
3）撒点有效性取决于撒点密度，撒点密度取决于计算效率
4）撒点不一定每个网格都要有点，有些空格也可以是没有点，其为了减低采样频率。这些方式，应该根据实际项目来思考的，没有孰优孰劣一概而定的。

思考：
Everything is trade-off?平衡，并不是找某个最优点或者速度最快的解，而是在效率和结果上取一个平衡的解
No model is perfect,but useful.无人车很难找到一个最优的解，每个模型都有其优势和劣势；充分利用优势和劣势，逐步找到当前环境下的最优解

---

加油