Fisher线性判别分析以及python实现

线性判别函数基本概念

我们主要讨论在两类情况下判别函数为线性的情况，这里给出一般情况：$g(\mathbf{x})={\mathbf{w}}^{\mathbf{T}}\mathbf{x}$+$w_0$
式子中$\mathbf{x}$为d维样本向量，$\mathbf{w}$为权向量，如下：
$$\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_d\end{array}\right]，\mathbf{w}=\left[\begin{array}{c}{w}_1\\ w_2\\ ⋮\\ w_d\end{array}\right]$$
$w_0$为一个常数，称为阈值权
令
$$g(\mathbf{x})={\mathbf{g}}_1(\mathbf{x})-{\mathbf{g}}_2(\mathbf{x})$$
设${\mathbf{x}}_0$为一个待分类样本，我们可以通过比较$g({\mathbf{x}}_0)$与0的大小来区分此样本属于哪一类

Fisher线性判别分析基本思想

Fisher线性判别分析的基本思想是把所有样本向某一一维向量上投影，使得同一类样本的投影点尽可能集中，而不同类的样本投影点之间距离比较远，如图：

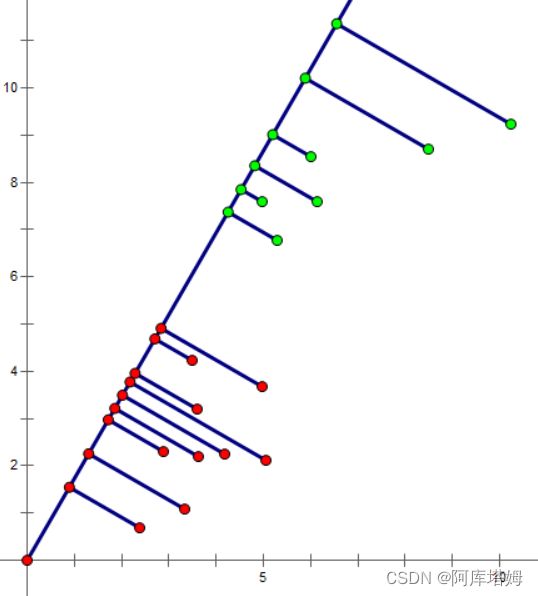
而如何定量分析找到这一最佳投影方向则是我们下面需要进行的任务

最优方向推导过程

在原样本空间中，设共有$N$个样本，属于第一类${\Psi }_1$的有$N_1$个，属于第二类${\Psi }_2$的有$N_2$个，每个样本都为一个d维向量，如之前所述。为了方便计算我们定义一些量：
类均值向量：
${\mathbf{m}}_{\mathbf{i}}$=$\frac{1}{N_i}{\sum }_{x_j\in {\Psi }_i}^{}{\mathbf{x}}_{\mathbf{j}},$ $i=1,2$
各类的类内离散度矩阵：
${\mathbf{s}}_{\mathbf{i}}={\sum }_{{\mathbf{x}}_{\mathbf{j}}\in {\mathbf{\Psi }}_{\mathbf{i}}}^{}({\mathbf{x}}_{\mathbf{j}}-{\mathbf{m}}_{\mathbf{i}})({\mathbf{x}}_{\mathbf{j}}-{\mathbf{m}}_{\mathbf{i}}{)}^{\mathbf{T}},$ $i=1,2$
总类内离散度矩阵：
${\mathbf{S}}_{\mathbf{w}}={\mathbf{S}}_1+{\mathbf{S}}_2$
类间离散度矩阵：
${\mathbf{S}}_{\mathbf{b}}=({\mathbf{m}}_1-{\mathbf{m}}_2)({\mathbf{m}}_1-{\mathbf{m}}_2{)}^{\mathbf{T}}$
而在投影之后，变为如下各量：
样本：
$y_i={\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}},$ $i=1,2,\cdots ,N$
两类均值：
$\widetilde{m_i}={\mathbf{w}}^{\mathbf{T}}{\mathbf{m}}_{\mathbf{i}},$ $i=1,2$
内离散度：
$\widetilde{S_i^2}={\sum }_{y_j\in {\Psi }_i}(y_j-\widetilde{m_i}{)}^2,i=1,2$
总类内离散度：
$\widetilde{S_w}=\widetilde{S_1^2}+\widetilde{S_2^2}$
类间离散度：
$\widetilde{S_b}=(\widetilde{m_1}-\widetilde{m_2}{)}^2$
有了以上的定义，我们的目标可以写为如下：
$$max{J}_F(w)=\frac{\widetilde{S_b}}{\widetilde{S_w}}$$
进一步推导可得：
$$\widetilde{S_b}={\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{b}}\mathbf{w}$$
$$\widetilde{S_w}={\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{w}$$
由于我们仅仅关心的是$\mathbf{w}$的方向而并不关心其幅值，因此我们可以假定分母为常数而使分子尽量大，也就变为如下准则：
$$max{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{b}}\mathbf{w},\mathbf{s}.\mathbf{t}.{\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{w}=\mathbf{c}\ne 0$$
利用拉格朗日乘子的有关知识，我们可以求解出最优方向的$\mathbf{w}$值：
$$\mathbf{w}={\mathbf{S}}_{\mathbf{w}}^{-1}({\mathbf{m}}_1-{\mathbf{m}}_2)$$

转换为判别函数

以上我们只是求解出了投影方向，如果要得到分类面，需要在投影之后的一维空间上确定一个分类阈值$w_o$,并采取如下决策规则：
$$若g(\mathbf{x})={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+{\mathbf{w}}_0\ge 0,则\mathbf{x}\in {\mathbf{\Psi }}_1,否则\mathbf{x}\in {\mathbf{\Psi }}_2$$
如果不考虑两类样本先验概率不同的情况，可以进行如下取值：
$w_0=-\frac{1}{2}(\widetilde{m_1}+\widetilde{m_2})$

完整代码

以下是利用python将以上过程实现的例子

#导入所需库：
import numpy as np
from matplotlib import pyplot as plt

#创建样本集：
X1 = np.array([[[1.2],[2.8]],
               [[1.9],[3.7]],
               [[2.5],[3.8]],
               [[4.8],[7.9]],
               [[5.6],[7.8]]])
X2 = np.array([[[9.7],[12.6]],
               [[10.8],[12.7]],
               [[13.7],[22.7]],
               [[7.48],[14.82]],
               [[11.23],[17.16]]])
N1 = X1.shape[0]
N2 = X2.shape[0]

#类均值向量：
m1 = np.array([[0],[0]])
for i in range(0,N1):
    m1 =m1+X1[i]
m1 = m1/N1
m2 = np.array([[0],[0]])
for i in range(0,N2):
    m2 =m2+X2[i]
m2 = m2/N2

#类内离散度矩阵：
S1 = np.zeros((2,2))
for i in range(0,N1):
    S1 = S1+np.dot(X1[i]-m1,np.transpose(X1[i]-m1))
S2 = np.zeros((2,2))
for i in range(0,N2):
    S2 = S2+np.dot(X2[i]-m2,np.transpose(X2[i]-m2))
Sw = S1+S2

#类间离散度矩阵：
Sb = np.dot(m1-m2,np.transpose(m1-m2))

#方向向量：
w = np.dot(np.linalg.inv(Sw),m1-m2)
print(w)

#投影后均值：
m11 = np.dot(np.transpose(w),m1)
m21 = np.dot(np.transpose(w),m2)
w0 = -(m11+m21)/2

#测试样本：
x_test = np.array([[3.42],[5.86]])
g = np.dot(np.transpose(w),x_test)+w0
if g>0:
    print('测试样本属于第一类！')
else:
    print('测试样本属于第二类！')


#可视化：
for i in range(0,N1):
    plt.scatter(X1[i,0],X1[i,1],c='r')
for i in range(0,N2):
    plt.scatter(X2[i,0],X2[i,1],c='b')
plt.scatter(x_test[0],x_test[1],c='g')
x = np.arange(0,15,0.01)
y = w[1]*x/w[0]
plt.plot(x,y,c='black')
plt.show()

运行结果如图：


最终将测试样本分入第一类，从图像上来看是合理的