C++ 2019-2022 CSP_J 复赛试题横向维度分析(下)
本文继续讲解第4题,第4题是压轴题,难度肯定是有的。也决定了是否能够拿到一等奖的关键题,也是区别能力高低的筛选题。
1.2022
1.1 题目
上升点列point
1.2 题目描述
在一个二维平面内,给定n个整数点(xi,yi),此外你还可以自由添加k个整数点。
你在自由添加k个点后,还需要从n+k个点中选出若个整数点并组成一个序列,使得序列中任意相邻两点间的欧几里得距离恰好为1而且横坐标、纵坐标值均单调不减,即 xi+1-xi=1,yi+1=yi 或 yi+1-yi=1,xi+1=xi 。请给出满足条件的序列的最大长度。
1.3 题目分析
直观感觉是一道类似于迷宫的试题。二维平面相当于一个矩阵,在此矩阵中,从一个点出发,查找到另一个点的最远距离。且搜索方向是确定的,要么向右,或者向上。可以使用深度搜索算法按步长值为 1查找任意两点之间的距离,然后从中找出最大长度。
因为不是所有点之间都是连续的,所以,搜索过程中是充许补点的。可以在搜索过程中出现断点后,试着向上或向右补点。本问题是求最值,也应该会想到使用动态规划。
1.4 编码实现
#include
#include
#include
using namespace std;
struct _pnt {
int x,y;
} a[1005];
int n,k,ans;
int f[105][105]; //dp 数组 f[i][z] 当共补了z个点的情况下,
//到第 i 个原始点能连成的最多的点的个数
int dis(int i,int j) { //从 j 到 i 共需要补的点的个数
return abs( a[i].x-a[j].x ) +abs( a[i].y-a[j].y ) -1;
}
bool cmp(_pnt p1,_pnt p2) {
if(p1.x==p2.x) return p1.y> n >> k;
for (int i = 1; i <= n; i ++) {
cin >> a[i].x >> a[i].y;
}
sort(a+1,a+n+1,cmp); // 排序,保证状态转移顺序的无后效性
for (int i = 1; i <= n; i++) {
int x = a[i].x, y = a[i].y;
for (int z = 0; z <= k; z++) {
f[i][z] = 1;
for (int j= 1; j <= n; j++) {
if (i != j && a[j].x <= x && a[j].y <= y) {//保证j在i的左下
int len = dis(i,j); // 从j到i共需要补Len个点
if (z >= len) {
f[i][z] = max(f[i][z],f[j][z - len] + len + 1);
// 多了Len+1个连续的点,+1表示第i个点自己
}
}
}
ans = max(ans,f[i][z] + k - z);// 从i把剩余的k-z个点疯狂延续出去
}
}
cout << ans;
return 0;
}
2.2021
2.1 题目
小熊的果篮
2.2 题目描述
小熊的水果店里摆放着一排 n 个水果。每个水果只可能苹果或桔子,从左到右依 次用正整数 1、2、3、.....、n编号。连续排在一起的同一种水果称为一个“块”。小熊要把这一排水果挑到若干个果篮里,具体方法是:
每次都把每一个“块”中最左边的水 果同时挑出,组成一个果篮。
重复这一操作,直至水果用完。
注意,每次挑完一果篮 后,“块”可能会发生变化。比如两个苹果“块”之间的唯一桔子被挑走后,两个苹果
“块”就变成了一个“块”。
请帮小熊计算每个果篮里包含的水果。
2.3 题目分析
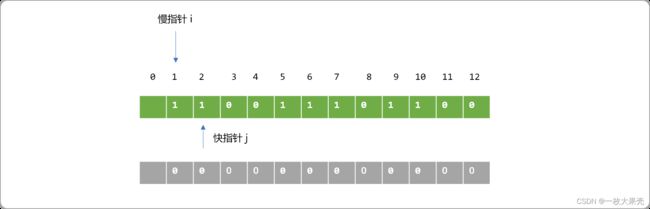
此题本质去重问题,可以有很多种方案,最简单的就是使用 2个数组,一个用来存储存原始数据,一个用来存储水果是否已经被选择的标志性数组。通过快慢指针选择出不重复的数据。
输出慢指针所指向位置的数据位置且在对应的标志位进行标记,移动快指针,如果快指针和慢指针所处位置数据不相同,则移动慢指针到快指针,且输出数据的位置。显然,这个是需要多轮去复。时间复杂度为 O(n2)。
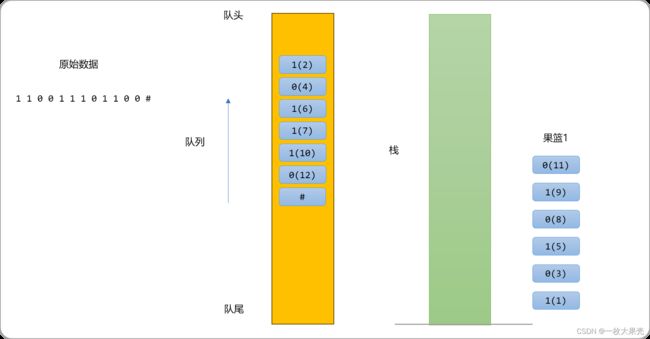
另一种方案是借助一个队列,一个栈来实现。首先需要一个结构类型,用来存储存水果的类型和原来的位置。
struct Sg {
//原来位置
int pos;
//水果类型
int type; // 1 苹果 0 桔子
};
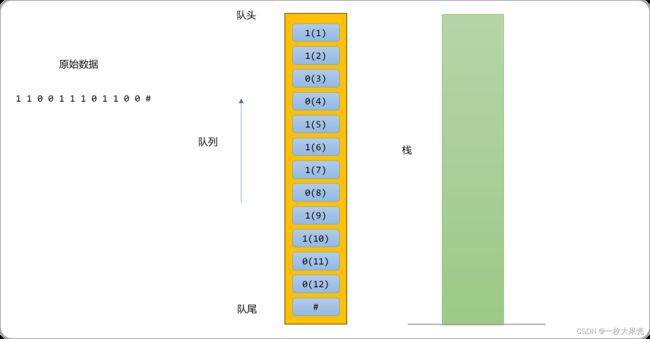
创建一个队列,把原始数据全部入队列。在队列的最后一个位置添加一个结束符号#。
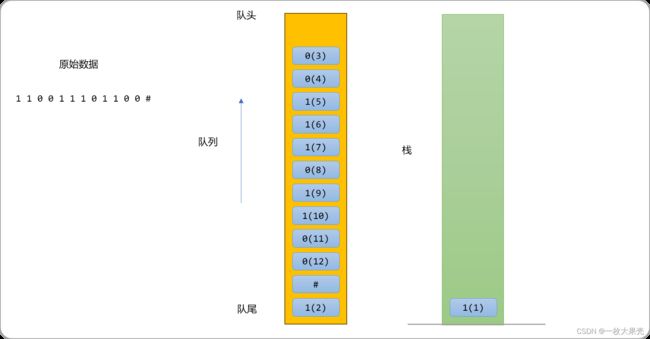
把队头数据放入栈中。
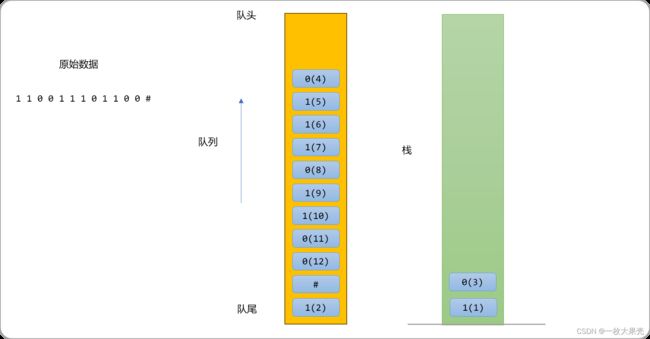
检查栈顶数据和队头数据是否相同,如果相同,把数据从队头拿出来后,再从除尾压入队列中。
如果栈顶数据和队头数据不相同,则把队头中数据压入栈中。
如此反复直到碰到 #符号。
然后输出栈中所有数据,继续从从队头中获取数据,直到队列中只剩下#符号。
时间复杂度可以控制中O(n)。可以遇到#号字符后,在栈中同样做一个标记。队列中的所有数据输出后,再统一输出栈中数据。
2.4 编码实现
#include
#include
#include
using namespace std;
//水果数量
int n;
struct Sg {
//原来位置
int pos;
//水果类型
int type; // 1 苹果 0 桔子
bool operator==(Sg & oth) {
return this->type==oth.type;
}
};
Sg sg[100];
//队列,可以使用数组
queue myq;
//栈,也可以数组
stack mys;
void init() {
int type;
//需要考虑 n=1 时的情况
for(int i=1; i<=n; i++) {
cin>>type;
sg[i]= {i,type };
//数据入队列
myq.push(sg[i]);
}
//添加结束符号,这里使用 -1 作为结束符号
myq.push({-1,-1});
//初始化栈
mys.push(myq.front()) ;
myq.pop();
}
void cal() {
//遍历队列
while(myq.size()!=1) {
//比较队头和栈顶数据
Sg dt=myq.front();
Sg zd=mys.top();
if(dt.type==-1) {
//复制一个结束符到栈中
mys.push( {-1,-1} );
myq.push(dt) ;
} else if(zd==dt ) {
//从队头出来,重新压入队列
myq.push(dt);
} else if(dt.type!=-1 ) {
//压入栈中
mys.push(dt);
}
myq.pop();
}
}
void result() {
stack tmp;
while(!mys.empty()) {
tmp.push( mys.top() );
mys.pop();
}
while(!tmp.empty()) {
Sg sg= tmp.top();
if(sg.type==-1) {
cout<>n;
init();
cal();
result();
return 0;
}
3.2020
3.1 题目
方格取数
3.2 题目描述
给定一个n行m列的二维矩阵每个格子有特定的权值需要从左上角走到右下角,每次可以向上、下、右走一步,但不能重复经过同一个格子,求走过的格子的权值和最大是多少。
3.3 题目分析
此题也可以看成一个迷宫问题。使用深度搜索可以实现,但时间复杂度可能会较高,使用动态规划解决应是首选。
本题无法通过一次性动态规划是推导出所有数据。如下图所示,根据题意,红色标记的单元格中的值需要通过上、左、下三个单元格中的已知值方能推导出来。
而下方标记为黄色单元格中的值则又需要红色单元格中的值方能推导入出来,显然是出现了先有鸡还是先有蛋的悖论。破坏了动态规划的无后序性法则。
这里可以采用先分离出不同方向的子状态值,然后综合子状态得到最终状态的思路。
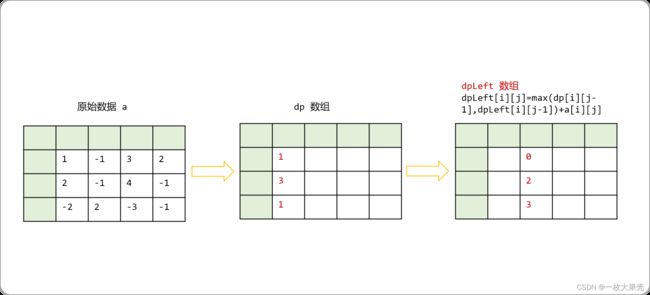
第一步:先找到动态规划的base case。对于第一列而言,因为只有一种路径可行,对第一列做前缀和操作。
第二步:根据 dp数组中的值由左向右推导出dpLeft数组中的状态值。已知左边的值,向右移动时,右边的值很容易推导出来。
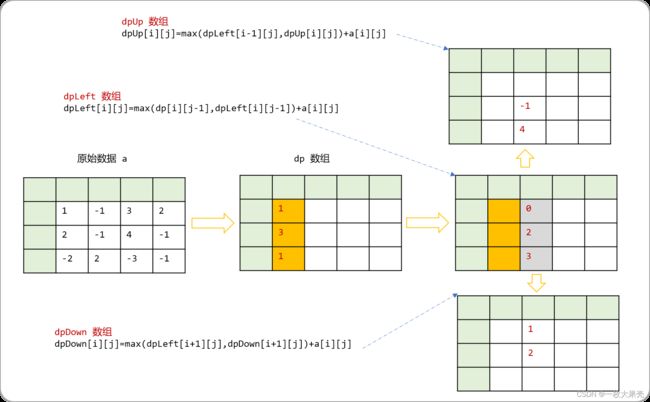
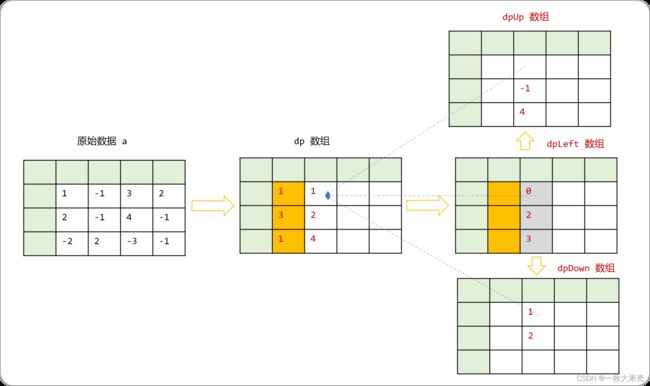
第三步:根据dpLeft中的值向上,向下推导出dpUp和dpDown数组中的值。
第四步:求解 dpLeft[i][j],dpUp[i][j],dpDown[i][j]中的最大值,填充在dp[i][j]中。
3.4 编码实现
#include
#include
#define ll long long int
using namespace std;
//方格
ll a[100][100];
//dp 数组
int dp[100][100],dpLeft[100][100],dpUp[100][100],dpDown[100][100];
//方格的长和宽
ll n,m;
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
cin>>a[i][j];
}
}
//初始化dp 表
for(int i=0; i<=n+1; i++) {
for( int j=0; j<=m+1; j++ ) {
dp[i][j]=dpLeft[i][j]=dpUp[i][j]=dpDown[i][j]=1>>30;
}
}
//计算 base case
for(int i=1; i<=n; i++) {
if(i==1)dp[i][1]=a[i][1];
else dp[i][1]+=dp[i-1][1]+a[i][1];
}
for(int j=2; j<=m; j++) {
for(int i=1; i<=n; i++ ) {
//子状态值 1
dpLeft[i][j]=dp[i][j-1]+a[i][j];
}
for(int i=2; i<=n; i++ ) {
//子状态值 2
dpUp[i][j]= max(dpLeft[i-1][j],dpUp[i-1][j] )+a[i][j];
}
for(int i=n-1; i>=1; i-- ) {
//子状态值 3
dpDown[i][j]= max( dpLeft[i+1][j],dpDown[i+1][j] )+a[i][j];
}
for( int i=1; i<=n; i++ ) {
dp[i][j]=max( dpLeft[i][j],dpUp[i][j] );
dp[i][j]=max( dp[i][j],dpDown[i][j] );
}
}
cout< 4.2019
4.1 题目
加工零件
4.2 题目描述
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有 n 位工人,工人们从 1~n 编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带。
如果 x号工人想生产一个被加工到第 L(L>1)阶段的零件,则所有与 x 号工人有传送带直接相连的工人,都需要生产一个被加工到第L-1 阶段的零件(但 x号工人自己无需生产第L-1 阶段的零件)。
如果 x号工人想生产一个被加工到第 1 阶段的零件,则所有与 x 号工人有传送带直接相连的工人,都需要为 x号工人提供一个原材料。
轩轩是 1 号工人。现在给出 q 张工单,第 i 张工单表示编号为 ai 的工人想生产·个第Li 阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来!
4.3 题目分析
无向图最短路径问题,使用广度搜索存储 1号工人到与之相连的其它工人之间的路径。
本题相当于问:1~ai,是否存在长度为li的路径;
4.4 编码实现
/*
*1. 求出1号点到每个点的最短奇数路径,和最短偶数路径;
2. q次询问,每次询问x号工人,如果生产len阶段的零件,1号点是否需要原材料;
如果1号点存在到x号点的最短奇数路径mins,且len是奇数,且len >= mins,1号点就需要提供原材料
偶数性质同上;
*/
#include
#include
using namespace std;
struct Ver {
int to;
int next;
};
Ver a[100];
int head[100],k=0;
queue myq;
int path[100][2];
bool vis[100][2];
int n,m,t;
void addEgde(int u,int v) {
k++;
a[k].to=v;
a[k].next=head[u];
head[u]=k;
}
int main() {
scanf("%d%d%d",&n,&m,&t);
int x,y;
for(int i=1; i<=m; i++) {
scanf("%d%d",&x,&y);
addEgde(x,y);
addEgde(y,x);
}
memset(path,0,sizeof(path));
path[1][0]=0;
if(head[1]==0)
path[1][0]=-1;
myq.push(1);
while( !myq.empty() ) {
int u=myq.front();
for(int i=head[u]; i!=0; i=a[i].next ) {
int to=a[i].to;
if( path[u][0]+1 5. 小结
2021、2023题目考察了动态规划,有一定难度,2020、2019的题目相对而言较简单。