数字图像处理实验记录二(直方图和直方图均衡化)
文章目录
- 一、基础知识
-
- 1,什么是直方图
- 2,直方图有什么用
- 3,直方图均衡化
- 4、原理代码实现
- 二、实验要求
-
- 任务1:
- 任务2:
- 三、实验记录
-
- 任务1:
- 任务2:
- 四、结果展示
-
- 任务1:
- 任务2:
- 五、反思,总结与收获
-
- 1,matlab函数怎么写:
- 2,坑,图像数据的类型是uint8:
- 3,均衡化后:
- 4,规定化后:
前言:由于踩了一些坑,进度就慢了很多,争取尽快赶上进度
一、基础知识
1,什么是直方图
在我看来,直方图就是展示一个图像中每个灰度的数量的图
如下图所示:
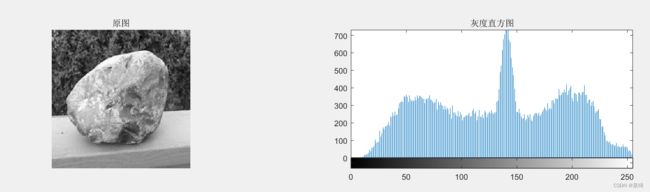
右边这张图就是灰度直方图,横坐标表示灰度,纵坐标表示这个灰度的数量
2,直方图有什么用
有什么用?目前看来就是有个展示作用。当然,我们可以点击这个链接查看直方图对应变化对图像的影响。
3,直方图均衡化
感觉直方图均衡化是一种对直方图进行调整的方法,将现在的直方图按照我们希望的函数排布。
要进行直方图均衡化,首先我们要求出原始图像的直方图,再计算积累直方图:
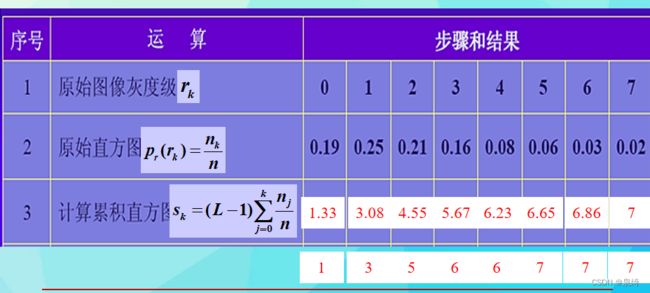
对应灰度级的积累直方图就是按照上面公式计算,最后将对应像素的值改成四舍五入后的值就实现了这个操作了
4、原理代码实现
原理:求出积累概率密度后,不能改变灰度像素的数量,就改变灰度值,改变原对应灰度的灰度值
对应积累概率密度*255 = 均衡后灰度

这里以一张灰度图为例的代码实现:
function [value,Sk] = his_teq(S,L)
% 进行均衡化操作
% S是输入的数据
[height,width] = size(S); %获取输入值的高和宽
if(~exist('L','var'))
L = 256; % 如果未出现该变量,则对其进行赋值
end
[count,x] = imhist(S,L);
p = count; %原始图像中各个灰度出现次数
size(count);
% 这里算每个灰度的概率
for i=1:L
p(i) = count(i)/height/width;
end
Sk = p;
for i=1:L %计算积累直方图
tmp = 0;
for j = 1:i
tmp=tmp+p(j);
end
Sk(i) = (L-1)*tmp;
Sk(i) = round(Sk(i));
end
% 替换
for i=1:height
for j=1:width
a = int16(S(i,j))+1; %这里是一个坑,我在这里犯了很多次
value(i,j) = Sk(a);
end
end
end
value = uint8(value);
end
二、实验要求
任务1:
使用函数imhist及histeq对原图进行直方图均衡化处理,同屏显示处理前后图像及其直方图,比较异同,并讨论为什么数字图像均衡化后其直方图并非完全均匀分布。
任务2:
使用函数histeq对原图进行直方图规定化处理,同屏显示处理前后图像及其直方图,比较异同。
三、实验记录
任务1:
使用函数imhist及histeq对原图进行直方图均衡化处理,同屏显示处理前后图像及其直方图,比较异同,并讨论为什么数字图像均衡化后其直方图并非完全均匀分布。
这里我们使用imhist()函数展示直方图,用histeq函数进行均衡化:
clc;
clear;
close all;
% 实验三 直方图均衡化
a1 = imread('图片1.png');
a2 = imread('图片2.png');
a2 = rgb2gray(a2);
a1_im = imhist(a1);
a2_im = imhist(a2);
a1_teq = histeq(a1);
a2_teq = histeq(a2);
figure('NumberTitle','off','Name','任务1');
subplot(241); imshow(a1);title('图片1');
subplot(242); imshow(a1_teq);title('图片1均衡化');
subplot(243); imshow(a2);title('图片2');
subplot(244); imshow(a2_teq);title('图片2均衡化');
subplot(245); imhist(a1);title('图片1的直方图');
subplot(246); imhist(a1_teq);title('图片1均衡化的直方图');
subplot(247); imhist(a2);title('图片2的直方图');
subplot(248); imhist(a2_teq);title('图片2均衡化的直方图');
任务2:
使用函数histeq对原图进行直方图规定化处理,同屏显示处理前后图像及其直方图,比较异同。
规定化步骤:
1,获取模板:a1_im = imhist(a1);像这样,就是先获取直方图
2,使用函数:a3 = histeq(a2,a1_im); 像这样,a2是图片,a1_im是直方图模板
代码:
clc;
clear;
close all;
% 实验三 直方图均衡化
a1 = imread('图片1.png');
a2 = imread('图片2.png');
a2 = rgb2gray(a2);
a1_im = imhist(a1);
a2_im = imhist(a2);
a1_teq = histeq(a1);
a2_teq = histeq(a2);
figure('NumberTitle','off','Name','任务1');
subplot(241); imshow(a1);title('图片1');
subplot(242); imshow(a1_teq);title('图片1均衡化');
subplot(243); imshow(a2);title('图片2');
subplot(244); imshow(a2_teq);title('图片2均衡化');
subplot(245); imhist(a1);title('图片1的直方图');
subplot(246); imhist(a1_teq);title('图片1均衡化的直方图');
subplot(247); imhist(a2);title('图片2的直方图');
subplot(248); imhist(a2_teq);title('图片2均衡化的直方图');
figure('NumberTitle','off','Name','任务2.1');
a3 = histeq(a2,a1_im);
subplot(221); imshow(a2);title('图片2');
subplot(222); imhist(a2);title('图片2的直方图');
subplot(223); imshow(a3);title('图片2规定化');
subplot(224); imhist(a3);title('图片2规定化的直方图');
figure('NumberTitle','off','Name','任务2.2');
a3 = histeq(a1,a2_im);
subplot(221); imshow(a1);title('图片1');
subplot(222); imhist(a1);title('图片1的直方图');
subplot(223); imshow(a3);title('图片1规定化');
subplot(224); imhist(a3);title('图片1规定化的直方图');
四、结果展示
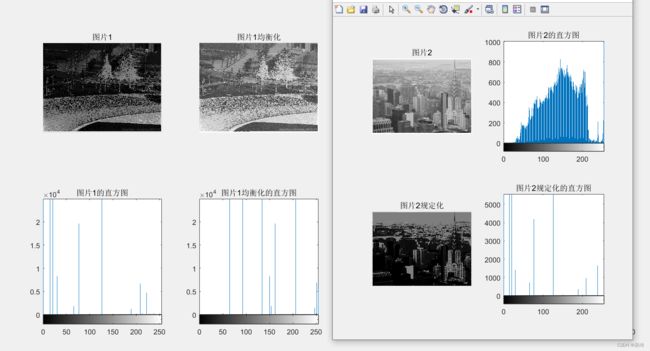
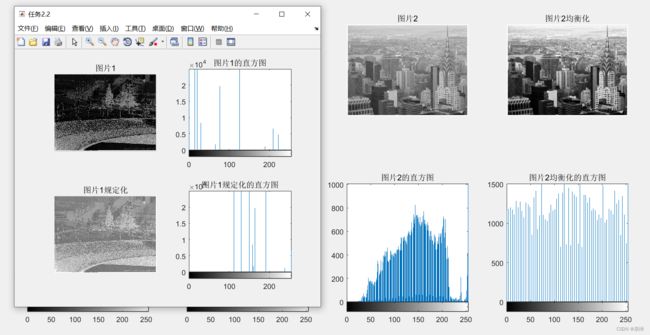
任务1:
任务2:
按图片1的直方图规定化图片2:
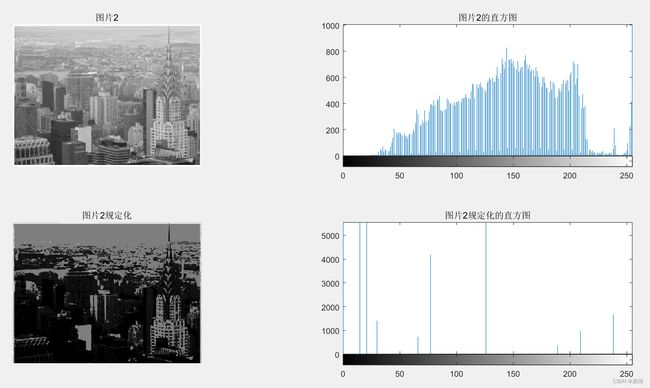
按图片2直方图规定化图片1:
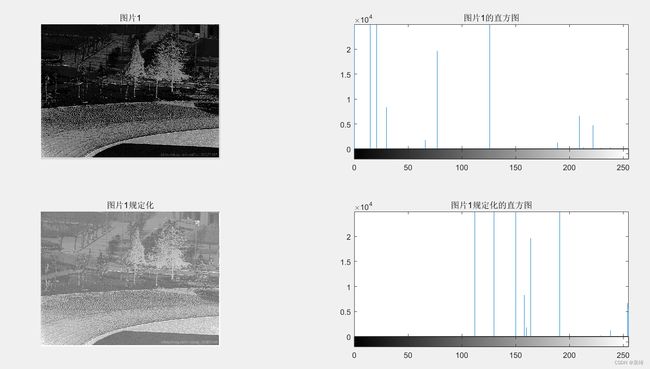
五、反思,总结与收获
1,matlab函数怎么写:
function [output] = name(input1,input2)
% 注释,说明函数的功能
output = 1 %内容
end %结束标志
2,坑,图像数据的类型是uint8:
图像数据类型是uint8,也就说明了这个没有符号,范围在0~255,所以如果你想取其作为下标或者进行计算的话需要注意。
如在这里:

S(i,j)可能会为255,当我们直接显示Sk(S(i,j)+1)时,S(i,j)=255,S(i,j)+1也等于255,因为matlab把它默认成了uint8数,所以在运算之前,我们要对其类型进行改变,这样才能运算
3,均衡化后:
均衡化后,其结果并不会如我们想象那样那么均衡,往往会如以下:

这个是按256个灰度值进行均衡化的
为什么数字图像均衡化后其直方图并非完全均匀分布呢?在我看来,其实是因为原图像的直方图本来就不是很均衡,甚至有突出的地方,在后续计算概率密度直方图时,哪个灰度值的数量多,对应的概率也就大,这样也就导致了均衡化后的直方图变成和原图差不多的样子。