链表OJ2——倒数第K个结点-分割链表,回文链表,相交链表,环形链表和随机指针链表深拷贝问题
文章目录
-
- @[toc]
- ✨单链表查找中间结点
-
-
- 两次遍历链表法
- 快慢指针法
- ✨查找链表中倒数第K个结点
- ✨合并两个升序链表
-
-
- 归并排序合并链表
- ✨分割链表
-
-
- 双哨兵链表归类法
- ✨回文链表
-
-
- 逆序部分链表法
- ✨链表相交
-
-
- N次遍历判别法
- 长链表走差距步法
- ✨环形链表
-
-
- 快慢指针探测环形链表
- 拓展题:快慢指针相遇求入环点
- ✨随机链表深拷贝
-
-
- 中间结点插入遍历法
- ⭐后话
文章目录
-
- @[toc]
- ✨单链表查找中间结点
-
-
- 两次遍历链表法
- 快慢指针法
-
- ✨查找链表中倒数第K个结点
- ✨合并两个升序链表
-
-
- 归并排序合并链表
-
- ✨分割链表
-
-
- 双哨兵链表归类法
-
- ✨回文链表
-
-
- 逆序部分链表法
-
- ✨链表相交
-
-
- N次遍历判别法
- 长链表走差距步法
-
- ✨环形链表
-
-
- 快慢指针探测环形链表
- 拓展题:快慢指针相遇求入环点
-
- ✨随机链表深拷贝
-
-
- 中间结点插入遍历法
-
- ⭐后话
链表定义
typedef int Etype;
typedef struct Singly_linked_list
{
Etype data;
Singly_linked_list* next;
}SgL;
本章主要采用前序章节详细讨论过的单链表结构和基本功能函数接口,详情请参考数据结构——链表及相关详细功能实现(万字整理)_VelvetShiki_Not_VS的博客。
✨单链表查找中间结点
题目来源:876. 链表的中间结点 - 力扣(LeetCode)
给定一个单链表,要定位处于中间位置的结点,因为是单链表,一个结点的结构体中只有数值域和指向后继结点的指针域,没有指向前一个结点的前驱指针(非双向链表),所以不能像顺序表根据下标和两个变量分别从收尾向中间遍历,当前一个变量下标不大于后一个变量下标时就可以定位出中间下标和数值。单链表一次遍历无法定位,有两种解题思路:
两次遍历链表法
定义Tail结点指针遍历链表,并创建计数变量count初始化为0,每经过一个结点count++,直到Tail遍历置空时结束循环,将count除以2得到偶数个结点链表的中间第一个结点位置或奇数个结点链表的中间结点位置,再次使Tail赋值链表头结点地址,遍历第二遍,此时遍历次数刚好为count/2次,则可将Tail指针指向链表中间结点所在位置。
快慢指针法
定义两个结点指针Fast和Slow,均以链表头结点地址赋值,都遍历链表,但两者遍历速度不同。快指针Fast一次走两个结点位置,即Fast必定提前到达链表末尾,慢指针每循环一次走一个结点位置。这样当快指针走到链表末尾时,慢指针刚好走到链表的中间位置,因为快指针走过的结点路程总是慢指针的二倍,当快指针遍历完链表,慢指针恰好走了快指针一半路程,即链表的中间位置。
快慢指针算法找中间结点
Etype FindMid(SgL* Head) //查找中间结点算法
{
assert(Head);
SgL* Fast = Head; //定义快指针,一次走两个结点
SgL* Slow = Head; //定义慢指针,一次走一个结点
while (Fast->next && Fast->next->next) //当快指针的下个结点为空或下下个结点为空时停止循环
{
Fast = Fast->next->next;
Slow = Slow->next;
}
if (Fast->next == NULL) //快指针下个结点为空时返回慢指针指向的结点数值
{
return Slow->data;
}
else if (Fast->next->next == NULL)//快指针下下个结点为空时返回慢指针的后继指针指向的结点数值
{
return Slow->next->data;
}
return NULL;
}
-
函数传实参链表头地址并返回链表的结点数值,此处采用assert断言空链表,没有结点的链表没有查找中间结点的意义,但若使代码拓展性更强,也可以将assert断言空链表改为判断并返回NULL。
-
快慢指针初始化为非空链表头地址,并分别在每次循环中移动两步和一步,循环判断条件为当快指针的后继或后后继为空时停止循环,且前者代表链表有奇数个结点,后者代表链表有偶数个结点,根据情况返回慢指针当前或后继结点的数值即可。
✨查找链表中倒数第K个结点
题目来源:面试题 02.02. 返回倒数第 k 个节点 - 力扣(LeetCode)
秉承上题思路,将查找中间结点改换为查找链表中倒数第K个结点的值并返回,此时可以最直观想到的方法同样为遍历两次链表,第一次遍历让count计数数出链表中的结点总个数max,并用max减去K可得到需要找到的结点位置,即上题的二次遍历法。但该题同样可以采用快慢指针法来寻找该结点。
快慢指针找倒数结点算法
Etype LastKVal(SgL* Head, int k) //查找倒数第k个
{
assert(Head);
SgL* cur = Head;
int count = 0;
while (cur) //遍历链表找k值范围
{
cur = cur->next;
count++;
}
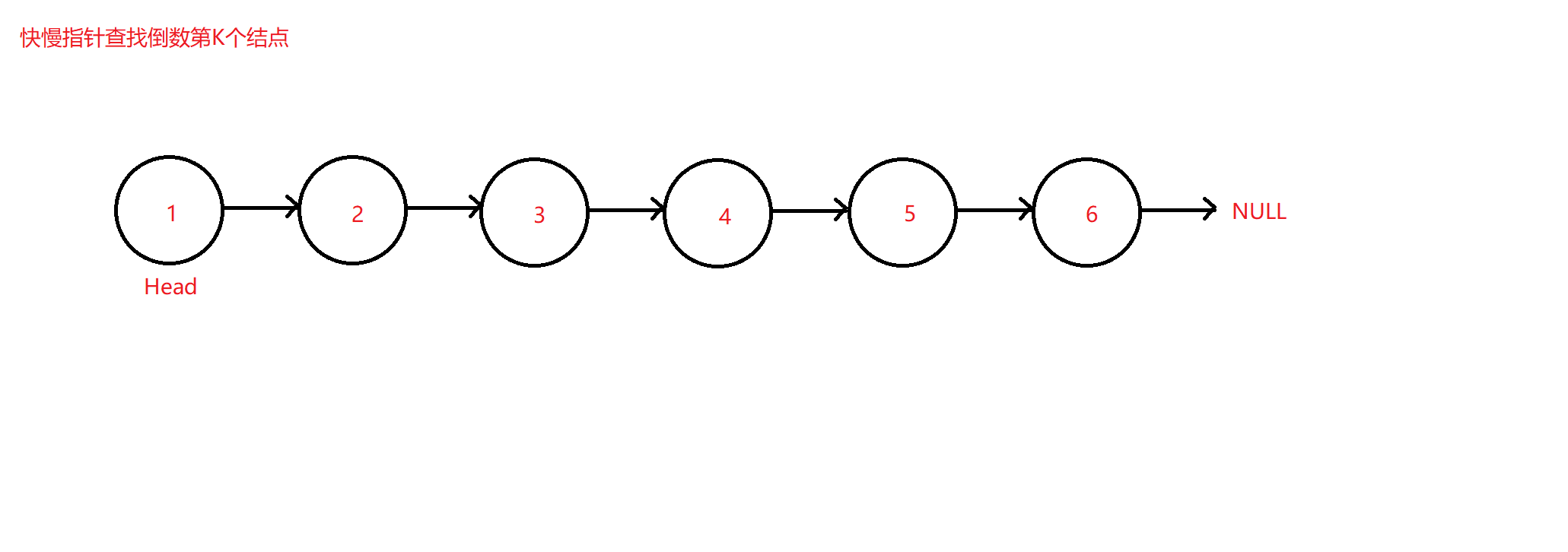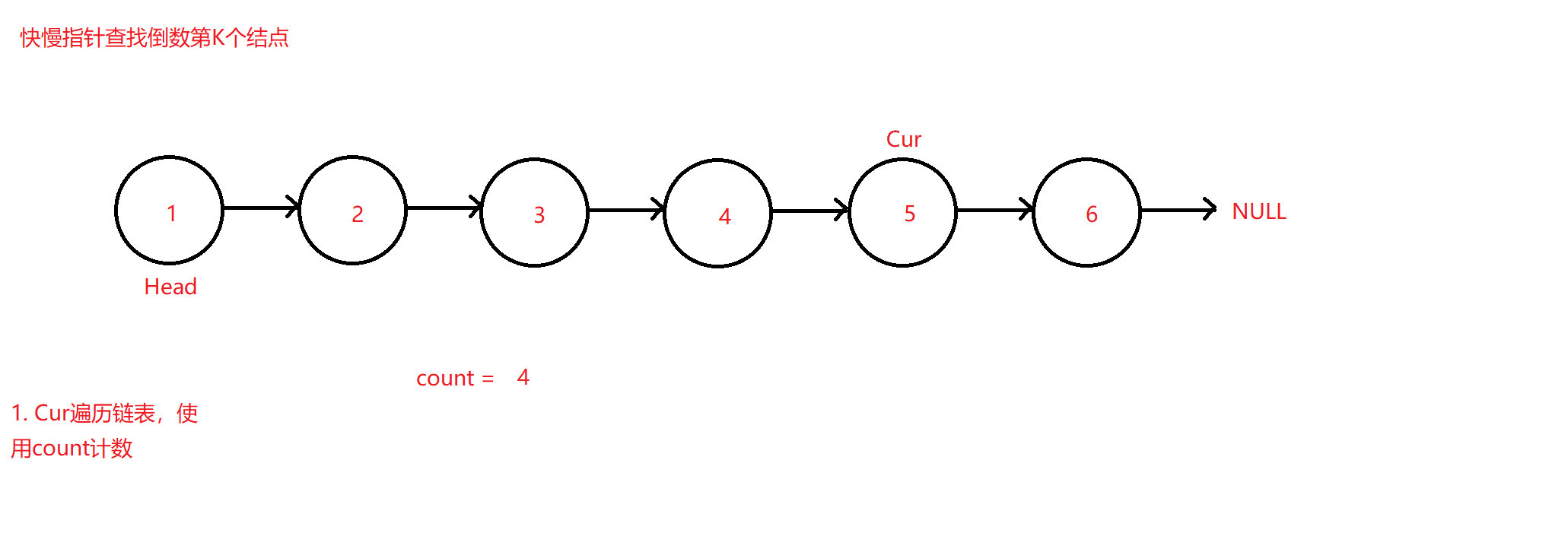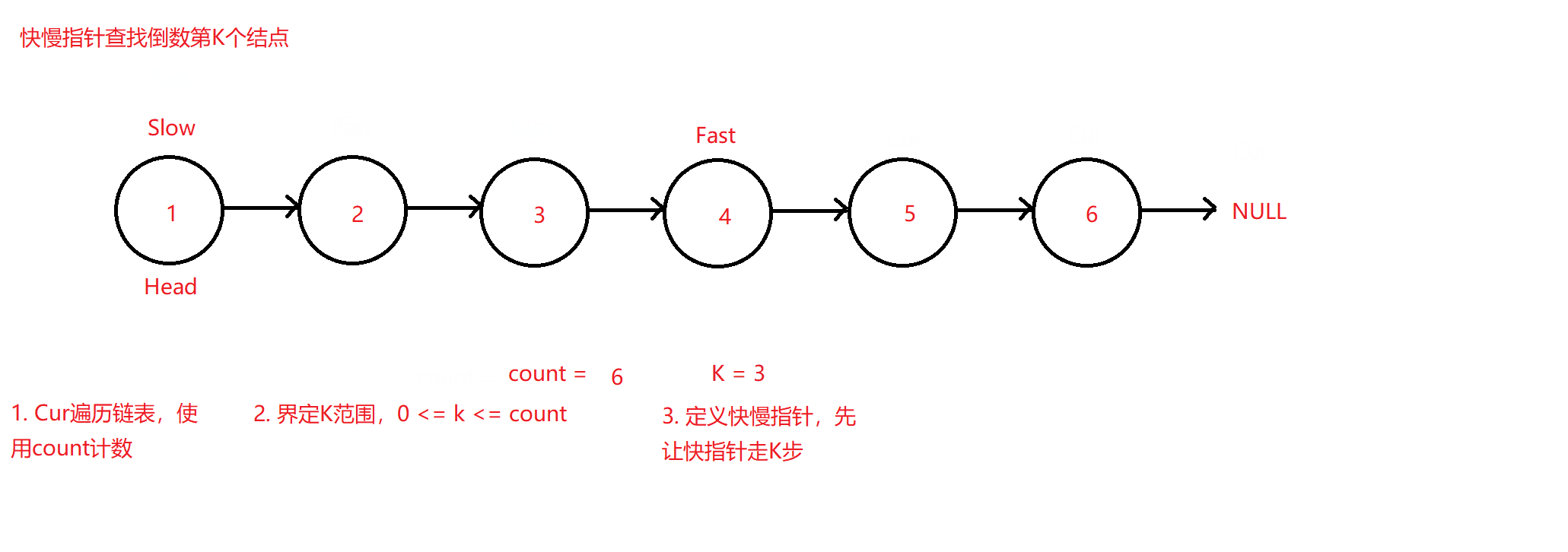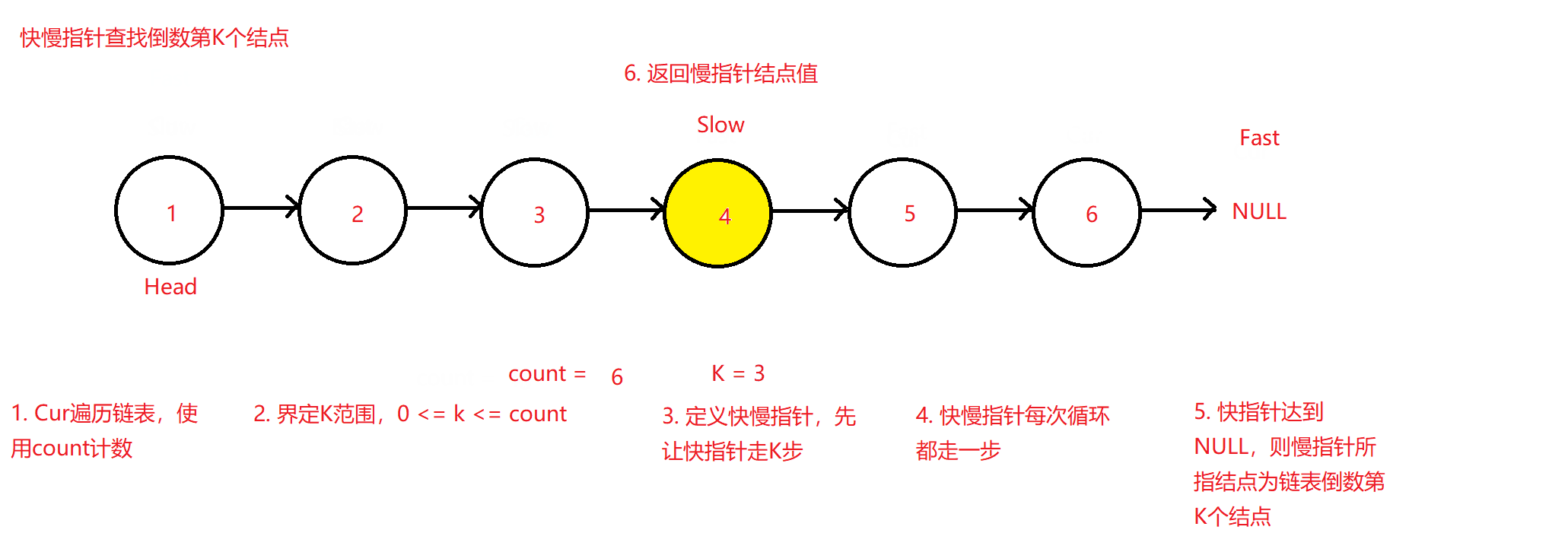
assert(k >= 0 && k <= count); //断言k的值范围必须在0到结点数之间
if (k == 0) //当倒数第0个时,返回头结点值
{
return NULL;
}
else
{
SgL* fast = Head;
SgL* slow = Head;
while (k--) //让快指针先在链表中走k步
{
fast = fast->next;
}
while (fast) //当快指针走到NULL,此时慢指针指向结点值即倒数第k个结点值
{
slow = slow->next;
fast = fast->next;
}
return slow->data; //返回该值
}
return 0;
}
-
函数传参传入头结点地址和需要查找的倒数第K个结点的位置,但因为该位置不确定,所以可能会超出链表个数范围,如仅存在3个结点的链表,而K为4,快指针将链表遍历完全也达不到该位置,所以需要界定K的有效范围。
-
先定义一个临时指针cur用于第一次遍历链表,使用count累加计算出当前链表的结点个数,断言传入函数的倒数位置K不能小于0(即倒数第0个,即NULL位置)且不能大于count(即不能遍历多余链表结点个数的位置)。
-
如果传入的参数K为0,则直接返回NULL,因为倒数第0个位置为空结点,此时值为NULL。如果不为0,则定义快慢指针Fast和Slow,先让快指针走K步,随后快指针和慢指针各走一步,当快指针循环到空值时,慢指针此时所处的值为倒数第K个结点所在位置,返回该结点值即可。
测试用例
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(2);
SgL* n3 = BuyListNode(3);
SgL* n4 = BuyListNode(4);
SgL* n5 = BuyListNode(5);
SgL* n6 = BuyListNode(6);
SgL* n7 = BuyListNode(7);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
n5->next = n6;
n6->next = n7;
printf("原链表结构为:");
Print(n1);
//调用函数并打印
int k = 0;
printf("查找到的倒数第%d个结点数值为:%d\n",k, LastKVal(n1, k));
int k = 3;
printf("查找到的倒数第%d个结点数值为:%d\n",k, LastKVal(n1, k));
int k = 5;
printf("查找到的倒数第%d个结点数值为:%d\n",k, LastKVal(n1, k));
int k = 8;
printf("查找到的倒数第%d个结点数值为:%d\n",k, LastKVal(n1, k));
观察结果
原链表结构为:1->2->3->4->5->6->7->NULL
查找到的倒数第0个结点数值为:0
查找到的倒数第3个结点数值为:5
查找到的倒数第5个结点数值为:3
Assertion failed: k >= 0 && k <= count, file D:\Code
可以看到函数结果符合预期,当倒数K的位置大于链表结点的有效范围时才会报错。
✨合并两个升序链表
题目来源:剑指 Offer 25. 合并两个排序的链表 - 力扣(LeetCode)
将两个非空的升序链表合并到一起,这个合并的新链表必须也按照升序的顺序从头结点到末节点排序。有两种思路可以解决该问题,因为两者都是升序链表,定义两个结点指针分别从头遍历两个链表到末尾,由头结点较小的一方作为新的起始结点,向后从小到大依次链接,即改变原来两个链表的指向。但该方法可能会在链接过程中将后续结点的地址丢失,且操作起来不容易控制。另外一种思路是使用归并排序的思路。
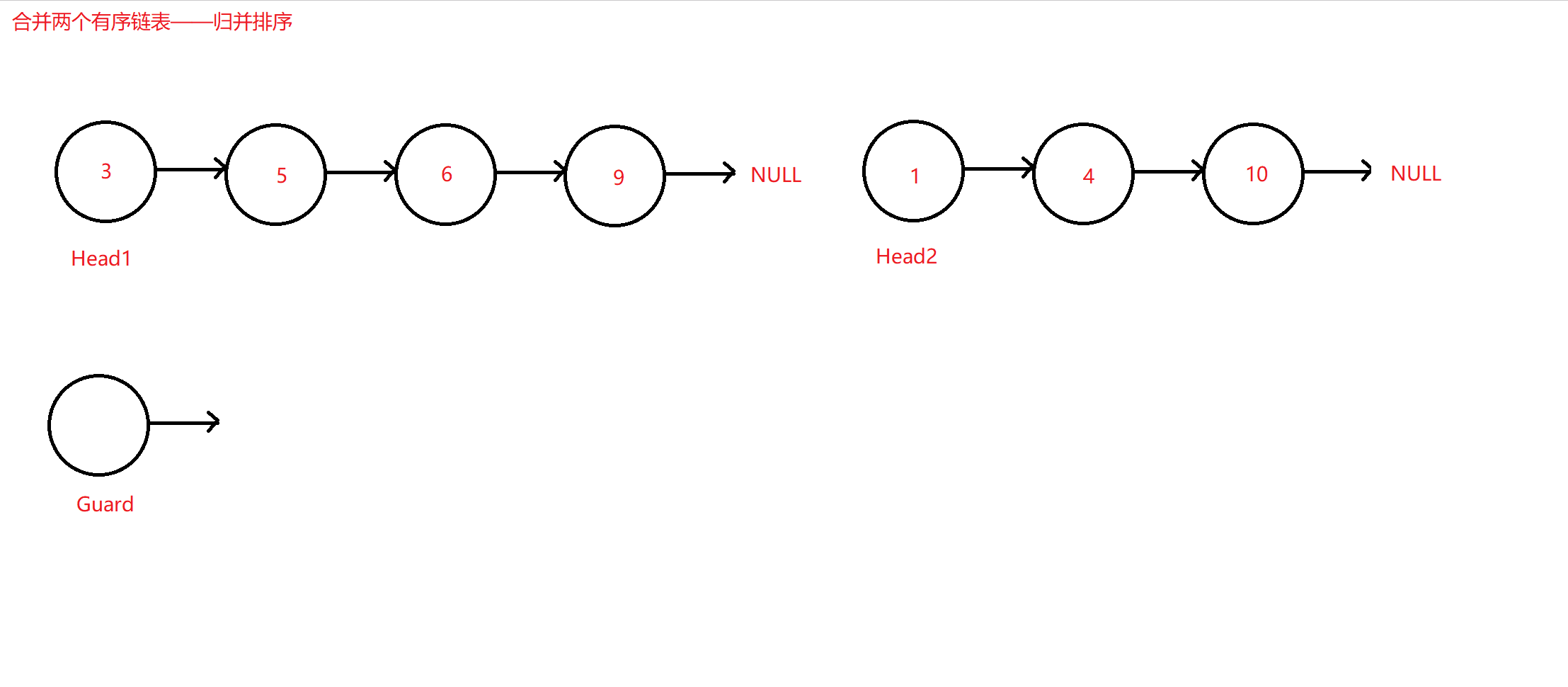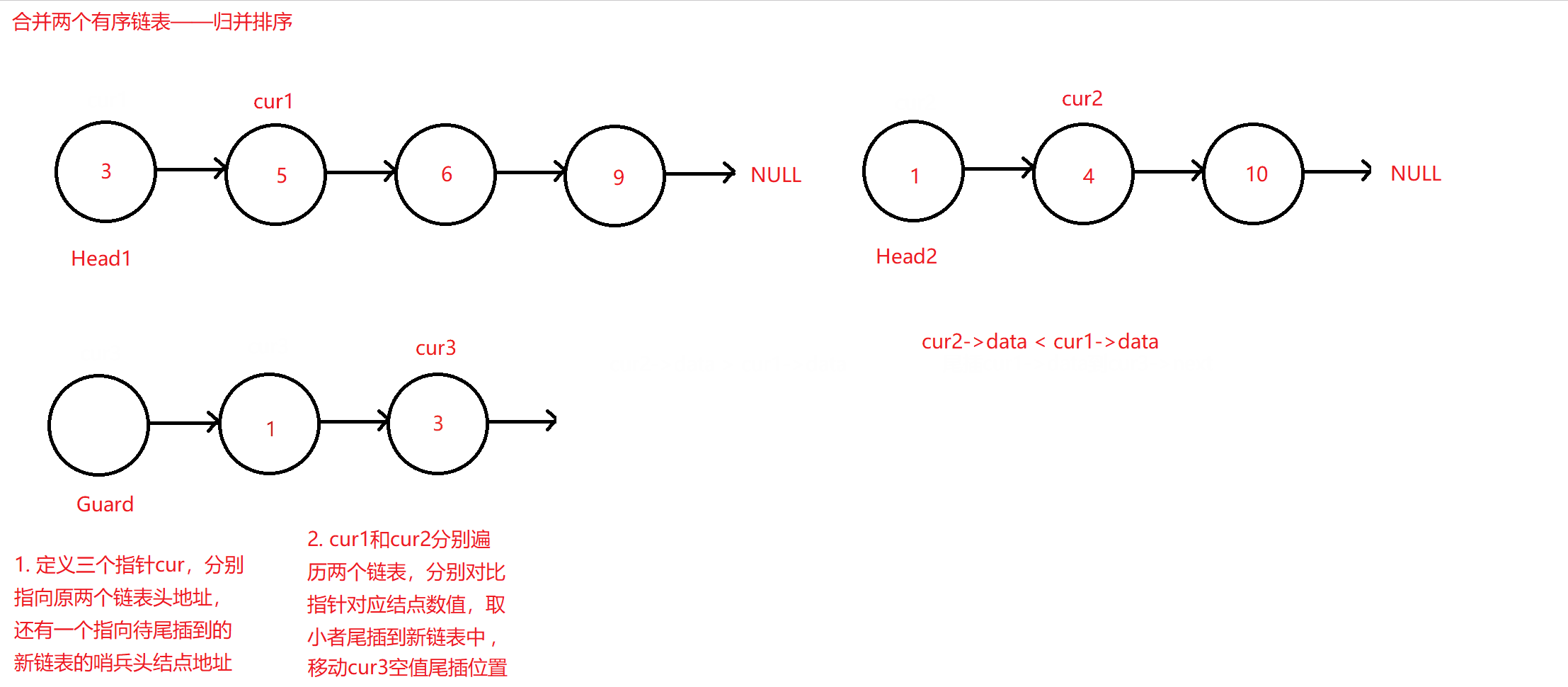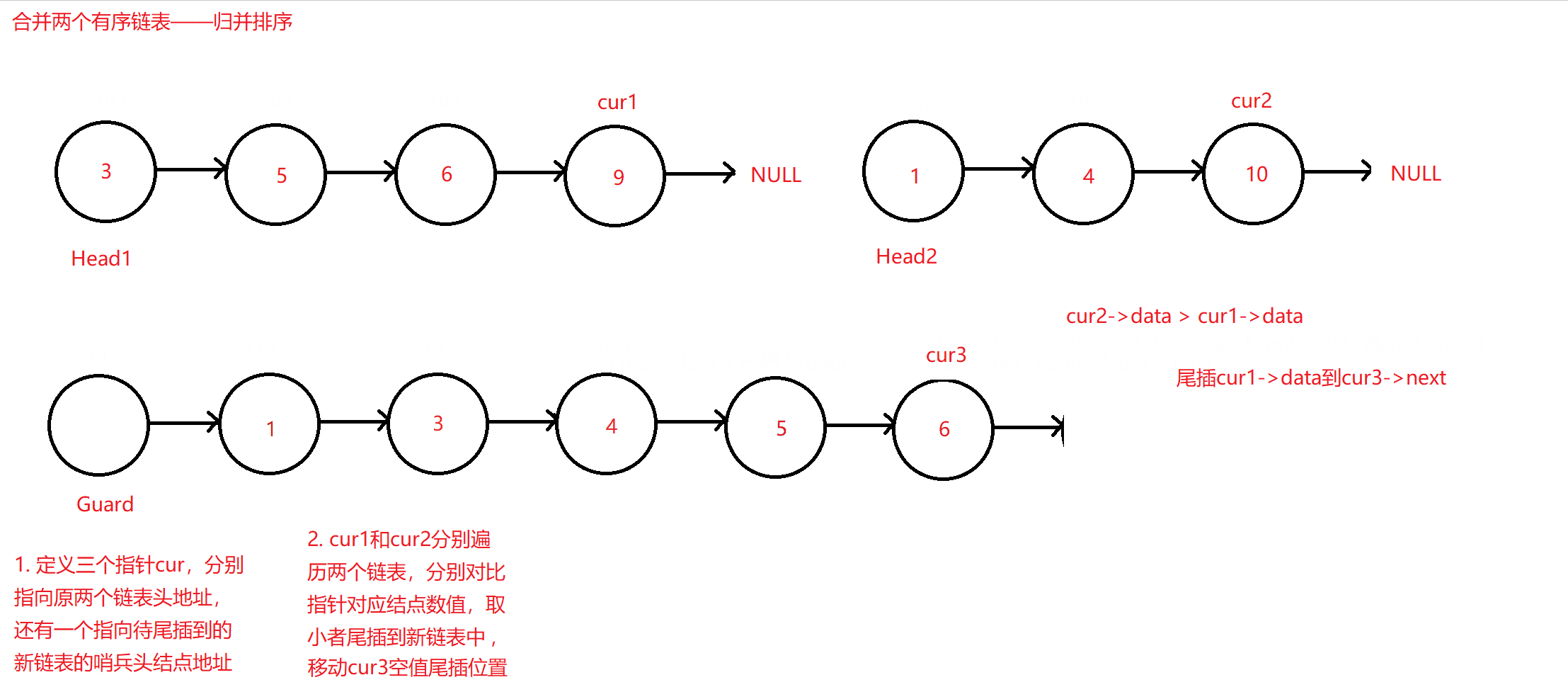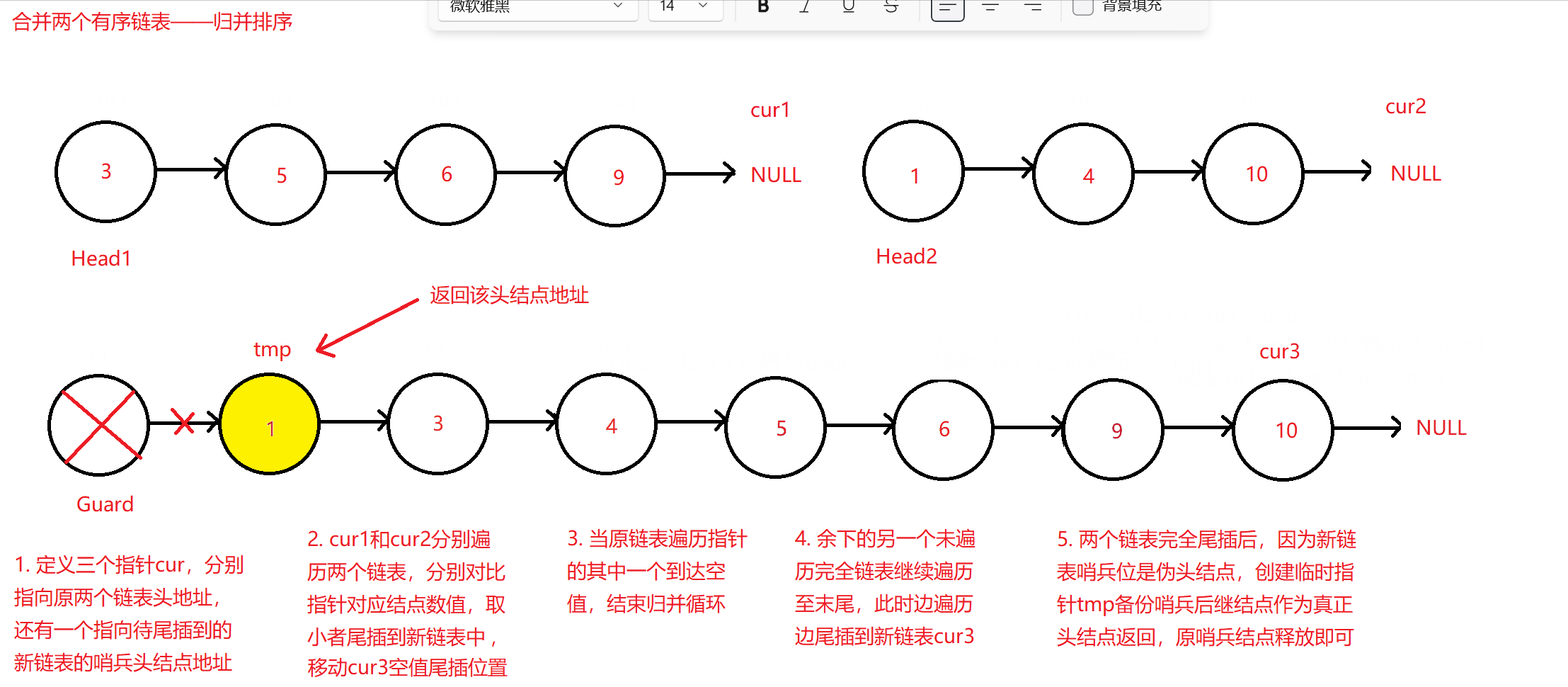
归并排序合并链表
定义遍历两个原链表的指针cur1和cur2,这两个指针分别从头结点,也即数值最小的结点遍历到末数值最大的节点。定义一个新的只带哨兵位伪头结点的链表,使用cur3指针指向它,其作用是方便之前两个指针边遍历边比较两个结点的数值大小,两者取一小者尾插到该新链表中。因为是升序尾插,原链表哪边取小之后,指针后移,而没有取小方的链表则保持不变;尾插到新链表的cur3指针也每尾插一次后移一次。
归并排序合并算法
SgL* Merging2SL(SgL* Head1, SgL* Head2) //合并两个有序链表函数
{
assert(Head1 && Head2);
SgL* Guard = BuyListNode(NULL); //创建哨兵头结点等待尾插
SgL* cur1 = Head1, * cur2 = Head2, * cur3 = Guard; //三个结点指针分别遍历两个原数组,还有一个负责尾插新链表
while (cur1 && cur2)
{
if (cur1->data <= cur2->data) //当第一个链表结点值小于第二个链表结点值
{
cur3->next = BuyListNode(cur1->data); //在新链表新开辟结点,并将原链表结点值放入
cur3 = cur3->next;
cur1 = cur1->next;
}
else //当第一个链表结点值大于第二个
{
cur3->next = BuyListNode(cur2->data);
cur3 = cur3->next;
cur2 = cur2->next;
}
}
if (cur1 != NULL) //当其中一个原链表先到达NULL,判断另一个链表是否尾插完毕
{
while (cur1)
{
cur3->next = BuyListNode(cur1->data);
cur3 = cur3->next;
cur1 = cur1->next;
}
}
else if (cur2 != NULL) //若另一个链表没达到NULL,则尾插该链表剩余全部值尾插到新链表后
{
while (cur2)
{
cur3->next = BuyListNode(cur2->data);
cur3 = cur3->next;
cur2 = cur2->next;
}
}
SgL* tmp = Guard->next;
free(Guard);
return tmp;
}
- 哨兵结点是不存储实际数值的链表“伪”头结点,该结点对于链表最方便之处在于不需要考虑头结点是否存在或被删除时需要改变头指针Head指向,特别是对于需要尾插的链表而言,第一个结点直接尾插到哨兵结点后继结点即可。如果不设立哨兵头结点,则插入的第一个结点必须由一个头结点指针Head指向,与直接可以插入到哨兵后继结点和直接释放删除所有已插入结点的带哨兵链表而言,稍微更复杂一些。
- 归并排序的基本思路就是两个链表取更小的一者,尾插到新的链表中,全部循环下来新的链表就集成并按序排序了两个链表的所有结点。这其中需要注意遍历链表结点的指针是否移动,仅有取了更小值结点的一方尾插后,需要向后移动一个结点以免重复取值。
测试用例
//链表1
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(7);
SgL* n3 = BuyListNode(10);
n1->next = n2;
n2->next = n3;
//链表2
SgL* n4 = BuyListNode(-1);
SgL* n5 = BuyListNode(3);
SgL* n6 = BuyListNode(4);
SgL* n7 = BuyListNode(7);
n4->next = n5;
n5->next = n6;
n6->next = n7;
printf("原两个链表的结构为:");
Print(n1);
Print(n4);
//合并链表
printf("合并的两个新有序链表为:");
SgL* Merge = Merging2SL(n1, n4);
Print(Merge);
观察结果
原两个链表的结构为:1->7->10->NULL 1->3->4->7->NULL
合并的两个新有序链表为:-1->1->3->4->7->7->10->NULL
因为合并链表函数中已将空链表断言为假,所以如果其中一个链表为空,合并函数将失效,该算法仅针对两个非空链表的合并。如果要解决空链表合并问题,也可以删除assert并仅输出另一升序链表即可。
✨分割链表
题目来源:面试题 02.04. 分割链表 - 力扣(LeetCode)
链表分割的描述为给定一个链表和值x,当链表中有结点中的数值小于该值x时,按照原来的顺序将这些结点重新排列到其他结点的前方,所有结点原来的顺序都不能打乱,比如存在链表4->3->2->1->NULL,给定x为3,将小于3的结点全部排到4之前,结果为2->1->4->3。该题本质并不是将一个链表分为独立的两个,而是按规则将特定值重新排列到头结点的前方,有两种解题思路,容易想到的一种是将比x小的结点寻找出来,全部按从左到右的顺序尾插到一个带哨兵结点的新链表中,然后将该链表末节点的后继将原链表链接起来,再擦除已经尾插过的原比x小的结点,最后释放头哨兵结点。该思路较为繁琐,既用到了尾插和查找和擦除函数,还需要不停考虑链表间结点的指向和地址问题。这里提供另一种思路,可以更方便解决该问题。
双哨兵链表归类法
定义两个带哨兵伪头结点的新链表,一个用于按原序存储原链表中比x小的结点,另一个存储剩余比x大的结点,当原链表由另一指针遍历完成后,再将小链表与大链表直接链接起来,释放哨兵结点即可。
双哨兵归类算法
SgL* SLSlicing(SgL* Head, int x) //分割链表函数
{
if(Head == NULL)
{
return NULL;
}
SgL* move = Head; //一个遍历原链表的指针
SgL* LessGuard = BuyListNode(NULL); //一个指向存放均比x值小的链表指针
SgL* BiggerGuard = BuyListNode(NULL); //一个指向存放均比x值大的链表指针
SgL* less = LessGuard, * big = BiggerGuard;
while (move) //结束条件为当原链表指针遍历到NULL
{
if (move->data < x) //若原链表当前结点值比x下,存入小链表中
{
less->next = BuyListNode(move->data);
less = less->next;
}
else
{
big->next = BuyListNode(move->data); //反之存入大链表中
big = big->next;
}
move = move->next;
}
less->next = BiggerGuard->next; //将小链表后继指针与大链表头哨兵结点后继的结点串联起来
SgL* tmp = LessGuard->next;
free(LessGuard); //释放大小链表的哨兵位
free(BiggerGuard);
return tmp; //将新串联的分割链表头结点地址返回
}
-
对于空链表的处理办法是直接返回空值,因为空链表不存在比x大或小的情况,所以传空返空即可,使用断言assert处理亦可。
-
同前例算法一样, 注意尾插链表使用的是新开辟的结点空间,BuyListNode是用户显性申请系统开辟的内存空间,而不是直接改变新链表的后继指向原链表,所以该算法的空间复杂度是O(N),而时间复杂度也为O(N),因为只遍历了一次原链表。
-
头哨兵结点因为在链表不存储实际有效数值,只是方便后续结点的尾插,所以在分类尾插好原链表结点后,要即使释放外函数不会用到的无意义结点,在此过程中需要注意要备份好哨兵的后继结点,因为如果先释放再返回的话,新头结点的地址会出现丢失的情况。
-
该算法中对于结点值与x相等的情况处理办法是归类于大链表中,即只有小于x的值放入LessGuard的小链表中,而大于或等于x的值存入大链表BiggerGuard中。
测试用例
//等待分割的原链表
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(4);
SgL* n3 = BuyListNode(3);
SgL* n4 = BuyListNode(2);
SgL* n5 = BuyListNode(5);
SgL* n6 = BuyListNode(2);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
n5->next = n6;
printf("原链表的结构为:");
Print(n1);
//规定待比较值x——case 1
int x = 3;
printf("分隔数值为%d,分割后的链表为:", x);
SgL* Division = SLSlicing(n1, x);
Print(Division);
//case 2
int x = 10;
printf("分隔数值为%d,分割后的链表为:", x);
SgL* Division = SLSlicing(n1, x);
Print(Division);
//case 3
int x = 0;
printf("分隔数值为%d,分割后的链表为:", x);
SgL* Division = SLSlicing(n1, x);
Print(Division);
观察结果
//case 1
原链表的结构为:1->4->3->2->5->2->NULL
分隔数值为3,分割后的链表为:1->2->2->4->3->5->NULL
//case 2
原链表的结构为:1->4->3->2->5->2->NULL
分隔数值为10,分割后的链表为:1->4->3->2->5->2->NULL
//case 3
原链表的结构为:1->4->3->2->5->2->NULL
分隔数值为0,分割后的链表为:1->4->3->2->5->2->NULL
可以注意到只有分割数值介于链表结点数值最大和最小范围内时才会出现分割情况,而输入比较的数值x如果比链表数值都大或都小时,就会全部插入到大链表,或小链表中,以至于出现链表似乎没有被分割过的情况。
✨回文链表
题目来源:234. 回文链表 - 力扣(LeetCode)
回文链表是一种特殊的链表结构,其前半部分与后半部分由中间结点(奇数个结点链表)或中央轴对称,比如有如下链表1->2->3->2->1,该奇数个链表由结点为3左右对称,而也有偶数个链表5->7->7->5,由中间左右各结点两两对称,即为回文结构。本题规定求一个链表是否为回文链表的算法时间复杂度为O(N),即仅遍历原链表就需要完成是否为回文结构的判断。
有两种解题思路,最容易想到的一种方法为遍历一遍原链表,并使用count记录下结点的个数,根据count计数单独开辟一个对应容量的数组,再次遍历原链表,将每个值对应存储数组下标中,存储完毕后首尾下标两两对比是否相等,并向中间靠拢,直到前下标不大于后下标时,如果都不出现前后两个值都不相等的情况,就可以判断是回文链表,是一种间接通过顺序表数值求解回文结构的思路,但弊端是开辟了N个容量的顺序表空间,时间和空间复杂度均为O(N)。以下提供另一种时间复杂度O(N),空间复杂度为O(1)的算法。
逆序部分链表法
将一个非空链表由中间结点为界限,将前后分为两部分,再将链表的后半部分逆序,如果前半部分的每个结点值都与逆序过的后半部分的每个结点值相同,则可判断该链表为回文链表,返回真,反之返回假。
-
该算法将链表总体分为三大类,如果传入回文判断函数的链表为空或者仅有一个结点,则直接判断该链表为回文结构,因为无结点链表和一个结点的链表都满足回文的要求。另一类是具有偶数个结点的链表,因为该算法需要将链表以中间结点为界的后半部分链表逆序,并且逆序完成后需要收尾两两比较结点值,且奇偶链表在中间结点的处理和指向上有所不同。
-
链表具有偶数个结点,经过快慢指针寻找后找到由慢指针slow指向中间的第二个结点,由该结点传入逆序链表函数,该函数已在之前探讨过,链接如下,经过逆序处理后原链表的末结点变为了新逆序的链表头结点,而慢指针slow指向的结点为逆序后链表的末节点,其后继指向NULL;同时slow指向的该结点并没有与前半部分链表独立出来,同样由整体链表的中间结点第一个的后继所指向,所以就出现了前半部分链表的结点数量总比后半部分链表结点数多一个的情况(偶数个结点的链表特有情况),但因为需要比较由中间第二个结点分隔开的前后链表的收尾值,所以将循环的比较条件设定为当cur1循环到中间第二个结点时就结束循环,以免左边链表多出的一个与右逆序链表空值比较,造成回文结构判非的情况。
回文算法
bool PalinDrome(SgL* Head) //判断一个链表是否为回文
{
if (Head == NULL || Head->next == NULL) //若为空链表或仅有一个结点的链表,返回真
{
return true;
}
SgL* fast = Head, * slow = Head; //定义快慢指针找中间结点
while (fast && fast->next) //快指针一次走两个结点,慢指针一次一个结点
{
fast = fast->next->next;
slow = slow->next;
}
SgL* ReverseHead = ReverseSL(slow); //调用逆序改链表指向函数,逆序链表中间节点后半部分,并用指针指向末节点
SgL* cur1 = Head; //两个指针分别指向前半部分和后半部分的逆序链表
SgL* cur2 = ReverseHead;
while (cur1 != slow) //前半部分与后半部分值的两两比较,循环比较结束条件为
{
if (cur1->data != cur2->data) //只要有其中一个不相等,就返回假
{
return false;
}
cur1 = cur1->next;
cur2 = cur2->next;
}
return true; //否则全部相等,返回真
}
- 该代码对于具有奇数和偶数个链表通用,即无论一个链表具有偶数个结点还是奇数个结点都可以判断并返回真假。对于偶数链表,为了验证上述理论的严谨和正确性,通过调试观察测试用例的中间结点值和其指向。
测试用例
//构造链表
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(2);
SgL* n3 = BuyListNode(3);
SgL* n4 = BuyListNode(3);
SgL* n5 = BuyListNode(2);
SgL* n6 = BuyListNode(1);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
n5->next = n6;
printf("原链表的结构为:");
Print(n1);
//判断链表是否回文
bool Judge = PalinDrome(n1);
if (Judge)
{
printf("是回文链表\n");
}
else
{
printf("不是回文链表\n");
}
观察结果
原链表的结构为:1->2->3->3->2->1->NULL
是回文链表
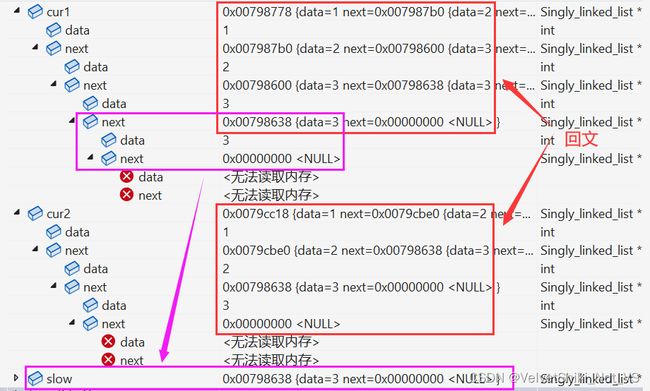
可以观察到,红框圈住的左右链表各3个结点的结点值首尾两两相等,已经可以判断为回文结构并满足要求。但左链表在第3个结点对比完成后的后继还显示了一个结点,由其地址0x00798638可知刚好与慢指针slow指向的结点,以及右链表的第三个结点地址相等,即多遍历了一次,这是由于逆序函数仅改变结点从右向左指向,而不改变原链表从左向右指向,导致左链表从头遍历至尾遇到右链表的末结点后继指向NULL才停止遍历和比较,由上原理图便可观察而得:

所以偶数链表在进行对比时需要手动控制对比的结点对数,命令左链表当cur1遍历至slow所指结点时就结束对比:
while (cur1 != slow) //前半部分与后半部分值的两两比较,注意循环对比的结束条件
{
if (cur1->data != cur2->data) //只要有其中一个不相等,就返回假
{
return false;
}
cur1 = cur1->next;
cur2 = cur2->next;
}
测试用例
//奇数链表
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(3);
SgL* n3 = BuyListNode(5);
SgL* n4 = BuyListNode(3);
SgL* n5 = BuyListNode(1);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
//n5->next = n6;
printf("原链表的结构为:");
Print(n1);
//回文判断
bool Judge = PalinDrome(n1);
if (Judge)
{
printf("是回文链表\n");
}
else
{
printf("不是回文链表\n");
}
观察结果
原链表的结构为:1->3->5->3->1->NULL
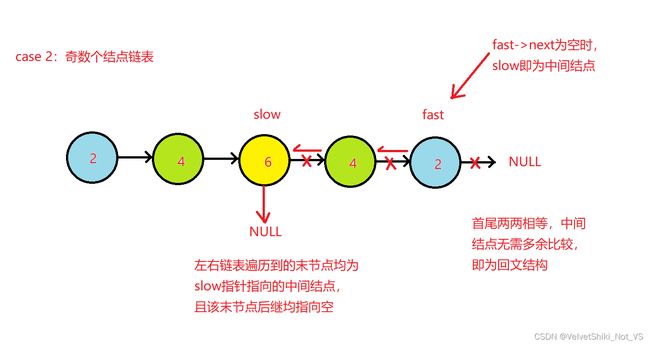
是回文链表
可看到奇数链表由中间结点分成左右两个后,它们由cur1和cur2遍历至的末结点均为slow指向的中间结点,且其后继均只指向空,再由参考代码中的循环对比结束条件可知,当cur1为中间结点slow时则结束对比,对于奇数链表而言,中间结点仅有一个,也就没有了对比意义,所以该代码对于奇偶链表的回文判断均是通用且正确的。
✨链表相交
题目来源:160. 相交链表 - 力扣(LeetCode)
两个链表可以是相互独立的,也可以共同有交点,共同的交点并不是体现在具有相同的结点值,而是体现在共同的结点地址上,因为具有相同值的结点可能有多个,比如链表3->3->3->3->3->3和链表3->3->3->3->3,它们的共同交点可能出现在任何位置,如头结点或中间结点甚至没有交点。所以只能通过地址来判断两个链表的共有结点,只要确定了该结点,则后续结点的地址和数值都是相同的(因为一个结点后继只能唯一指向另一个结点,所以不会出现链表交叉情况)。
N次遍历判别法
给定两个链表L1和L2,为了对比两个链表中存在的相同结点地址,需要逐个比较,即用L1中的每个结点和L2中的每个结点都比一遍,时间复杂度为O(N2),如果数据繁多,时间代价将会很大,所以此种算法不推荐。
长链表走差距步法
先遍历两个链表并记录两个链表的结点总个数length,计算出两者结点数量差Interval,再次遍历较长的一个链表,让其从头结点开始由指针指向先移动Interval个结点数目,然后短链表再从头向后与移动了几步的长链表一起向后遍历比较,如果长链表的某个结点刚好与短链表的某个结点地址与数值都相同,则该结点即为两链表的相交结点。
链表相交算法
SgL* CrossOver(SgL* Head1, SgL* Head2) //找两链表相交结点函数
{
if (Head1 == NULL || Head2 == NULL)
{
return NULL;
}
if (Head1 == Head2) //若传入的两个链表头结点地址相同,则头结点就相交且为同一链表
{
return Head1;
}
SgL* cur1 = Head1; //定义两个指针分别遍历原链表
SgL* cur2 = Head2;
int length1 = 0, length2 = 0;
while (cur1) //遍历两个链表求长度
{
cur1 = cur1->next;
length1++;
}
while (cur2)
{
cur2 = cur2->next;
length2++;
}
int Interval = length1 >= length2 ? length1 - length2 : length2 - length1; //算出长度差距
if (length1 >= length2)
{
cur1 = Head1;
while (Interval--) //让更长的链表先走k个结点
{
cur1 = cur1->next;
}
cur2 = Head2; //并让短链表的遍历指针重置回头部
}
else
{
cur2 = Head2;
while (Interval--)
{
cur2 = cur2->next;
}
cur1 = Head1;
}
while (cur1) //此时两链表长度相等
{
if (cur1 == cur2) //遍历链表并对比指针地址,相等则找到交点
{
return cur1;
}
cur1 = cur1->next;
cur2 = cur2->next;
}
return NULL; //否则返回空值
}
-
该函数传入了两个链表的头结点地址,如果两个链表均为空或一个为空另一个非空,则直接返回空,空链表之间或非空与空表间不存在相交结点。而如果两个头结点地址就已经相等,则表明传入该函数的两个参数头地址都指向同一链表,则返回该链表的头地址本身,即头结点地址就是它们的相交结点。
-
如果是非空的两个等长或不等长链表,均可通过该函数求出相交结点,需要注意两个链表的相交结点只能通过比较两链表中具有的第一个结点的相同地址,而不能通过数值来比较。
比较的方法已在上图与代码和注释中详细阐述,而最需要注意的点在于计算出的两链表结点数量差和让较长链表从头开始遍历时先移动数量差Interval步,再让短链表与长链表一起向后遍历找地址相同的结点。
-
如果两个相交链表的长度相等,算出结点差Interval为0,则两个等长链表都从头结点开始遍历,一直等到cur1 == cur2两结点地址相等时,直接返回该相交结点的地址,或直到两个等长链表遍历完都没有找到等地址结点,则两链表没有相交结点。
测试用例
//链表1
SgL* n1 = BuyListNode(5);
SgL* n2 = BuyListNode(5);
SgL* n3 = BuyListNode(5);
SgL* n4 = BuyListNode(5);
SgL* n5 = BuyListNode(5);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
//链表2
SgL* n6 = BuyListNode(5);
SgL* n7 = BuyListNode(5);
SgL* n8 = BuyListNode(5);
n6->next = n7;
n7->next = n8;
n8->next = n4;
printf("原两个链表的结构为:\n");
Print(n1);
Print(n6);
//链表判交
SgL* output = CrossOver(n1, n6);
if (output != NULL)
{
printf("两链表的相交结点为:%d,其地址为:0x%p\n", output->data, output);
}
else
{
printf("无交点\n");
}
观察结果
原两个链表的结构为:
5->5->5->5->5->NULL
5->5->5->5->5->NULL
两链表的相交结点为:5,其地址为:0x00718758
两个非等长链表在第一个链表的第四个数值为5,地址为0x00718758的结点处相交。
✨环形链表
题目来源:141. 环形链表 - 力扣(LeetCode)
环形链表,顾名思义,就是链表环绕成一个圈,其末节点的后继不指向空,而是继续指向链表内部的另外一个结点。对于环形链表的遍历会造成死循环,因为末节点的后继仍然指向其他结点,也就没有了末节点。对于一个链表可以通过环形判断算法来探测其是否带环,还可以在环形链表结构的基础上对其入环点进行检测和返回。环形链表的探测思路可以使用快慢指针的思想。
快慢指针探测环形链表
对于一个非空链表,为了判断其是否带环,即判断哪个结点的后继回头指向了之前的某个结点,需要定义快慢指针来判断。对于一个非环形链表而言,快指针一次移动两个结点,慢指针一次移动一个结点,因为链表是有穷的,所以慢指针永远追不上快指针,两者在同一时间对应的结点地址值不可能相等。而环形链表,对于快指针一次移动两个结点而言,慢指针一定追得上快指针,且两者地址和数值相等的时刻,它们所在的链表即为环形链表。
☣️快指针和慢指针可以相遇,但该相遇点并不一定是入环点,如上图case1,case2和case4都刚好在入环点相遇,但case3经过了入环点2后以后才相遇,所以该算法仅能判断一个链表是否带环,而不能判断入环点在哪里。
环形结构探测算法
bool Detect(SgL* Head)
{
if(Head == NULL) //空链表直接返回假,无环
{
return false;
}
SgL* fast, * slow; //定义快慢指针,均以非空链表头结点地址初始化
fast = slow = Head;
while (fast && fast->next) //如果快指针能走到链表尽头,则该链表无环
{
if (fast == slow) //如果快指针能被慢指针追上,则该链表一定有环
{
return true;
}
fast = fast->next->next; //快指针一次移动两个结点,慢指针一次一个
slow = slow->next;
}
return false;
}
-
环形链表中为什么慢指针一定能追得上快指针?快指针走的一定比慢指针块,进入环以后,假设慢指针与快指针刚开始相距N,两个指针每走一次,距离缩减1,即两者间距离从N,变为N-1, N-2, N-3, … 2, 1, 0,当N = 0时,快指针与慢指针相遇,则一定追得上。
-
慢指针进环后,慢指针一定会在一圈之内就会被快指针追上,因为进去后距离N就在缩减,相对距离一定在缩小而不可能错过,即使是快慢指针相距最远的情况,慢指针最多走半圈就会被快指针追上,因为快指针走的速度总是慢指针的两倍。
-
若快指针一次走3步,或更多步,可能追得上也有可能追不上慢指针(刚好超过慢指针而不会相等),此时快指针与慢指针的追及距离为偶数时才能追上,为奇数时可能再下一圈追得上(环数-1变为偶数),也可能永远追不上(环数-1一直为奇数)。
-
即使快指针能追上慢指针,两者所指向地址相等时的结点不一定为进入环前的一个结点(入环点),而有可能在环内的某个结点相遇。入环点的判定需要单独的算法来判断。
拓展题:快慢指针相遇求入环点
题目来源:142. 环形链表 II - 力扣(LeetCode)
秉承前例思路,一个非空有环链表的快慢指针在环内或入环点相遇是不确定的,假设两者在环内相遇,此时快慢指针指向同一结点,定义此点meet,若要寻找入环结点,不再移动快指针,另外定义一个自头向后遍历寻找入环结点的指针In,与慢指针同时开始继续向结点后继遍历(均每次移动一个结点),当慢指针slow与寻入环指针In在链表中相遇时,它们所指向结点就是入环结点。该思路可由数学公式L = (N-1)*C + (C-X)证明而得,其中L为链表中非环路结点数量,N为快指针在环中走过的圈数,C为环内的结点数,X为进入环内且被追上前走过的节点数。
链表环形判断和入环点检测函数综合
SgL* Enter(SgL* Head)
{
if(Head == NULL) //空链表直接返回空,无环且无入环点
{
return NULL;
}
SgL* fast, * slow, * In; //定义快慢指针和找入环点指针,均初始化为头地址
fast = slow = In = Head;
while (fast && fast->next) //快满指针找相遇点
{
if (fast == slow) //找到相遇点,则只动慢指针,并在头结点同时开始移动入环点检测指针In
{
printf("相遇地点为:%d\n", fast->data);
while (In != slow) //当检测指针与慢指针相遇时,此时的结点就是入环点
{
slow = slow->next;
In = In->next;
}
return In; //将入环结点地址返回
}
fast = fast->next->next;
slow = slow->next;
}
return NULL;
}
测试用例
//定义有环链表
SgL* n1 = BuyListNode(1);
SgL* n2 = BuyListNode(2);
SgL* n3 = BuyListNode(3);
SgL* n4 = BuyListNode(4);
SgL* n5 = BuyListNode(5);
SgL* n6 = BuyListNode(6);
n1->next = n2;
n2->next = n3;
n3->next = n4;
n4->next = n5;
n5->next = n6;
n6->next = n3;
//探测函数检测环结构
if (Detect(n1))
{
printf("有环\n");
}
else
{
printf("无环\n");
}
//检测入环点
SgL* p = Enter(n1);
Etype output = p->data;
printf("入环点地址为0x%p,其值为:%d\n", p, output);
观察结果
有环
相遇地点为:5
入环点地址为0x013A8720,其值为:3
✨随机链表深拷贝
题目来源:138. 复制带随机指针的链表 - 力扣(LeetCode)
单链表具有存储数据的数值域和存储下一节点的指针域两大部分组成,现有一种链表结点包含额外指向随机地址的指针,该指针可能无规律地指向链表中的其他结点,也有可能指向空值,或指向结点自己。
该类链表结点结构定义
typedef int Etype;
typedef struct Random
{
Etype data;
Random* next;
Random* random; //相比原单链表结构多了一个指向随机结点的指针域
}RD;
可以看出,该类链表结点主要包含三大结构:
存储数据的数值域data
指向下一结点结构体地址的后继指针域next
指向随机结点结构体地址的随机指针域random
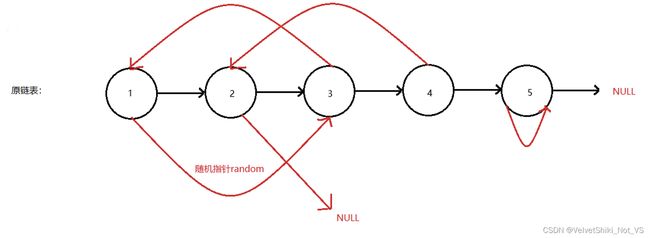
现有如下已定义好结构的带随机指针链表
RD* n1 = BuyRandom(1);
RD* n2 = BuyRandom(2);
RD* n3 = BuyRandom(3);
RD* n4 = BuyRandom(4);
RD* n5 = BuyRandom(5);
n1->next = n2;
n1->random = n3;
n2->next = n3;
n3->next = n4;
n3->random = n1;
n4->next = n5;
n4->random = n2;
n5->random = n5;
开辟带随机指针的链表结点函数
RD* BuyRandom(Etype x) //开辟随机指针结点
{
RD* NewNode = (RD*)malloc(sizeof(RD));
assert(NewNode);
NewNode->data = x;
NewNode->next = NULL;
NewNode->random = NULL;
return NewNode;
}
要求一比一复刻该链表到一个内存地址完全不同的新链表中,或称为链表的“深拷贝”。
中间结点插入遍历法
如果要对一个仅有数值域和后继指针域的单链表进行深拷贝,仅需边遍历一次原链表,边尾插到新链表即可,因为后继指针域唯一指向当前结点的后一个结点,是比较容易的事情。而该例中每个结点额外新增了一个随机指针域,如果仍采用遍历尾插的方式构造新带随机指针的链表,则可能会出现随机指向的结点不存在的情况。这里提供的算法引用了中间插入原随机指针链表的思路,大致将过程分为三个步骤:
-
循环开辟与原链表结点数量相同的新的带随机指针结点,根据对应值分别依次中间插入到原链表每个结点的后继,过程中需要不断改变指针指向,防止原链表丢失对后续结点的访问,该过程仅进行了对原链表结点的数值拷贝,以及完成了新开辟结点中间插入到原链表中,而并没有对随机指针域进行拷贝处理。
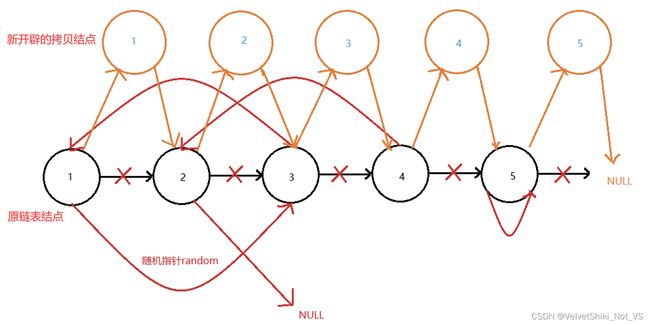
-
每个新拷贝结点的随机指针random指向的是:其上一个结点的随机指针指向的结点的后一个结点,即拷贝的结点随机指针域经由原链表随机指针的指向找到其应该指向的另一个拷贝结点,以一种间接通过原链表随机指针域的方式找到了拷贝结点指向,指向顺序和随机指针链接路径可由代码解释为:
while(cur) { if (cur->random == NULL) //如果原链表随机指针指向空 { cur->next->random = NULL; //则新拷贝结点的随机指针也指向空 } else if (cur->random == cur) //如果原链表随机指针指向该结点本身 { cur->next->random = cur->next; //则新拷贝结点的随机指针也指向其本身 } else //如果原链表随机指针指向链表中的其他原结点 { cur->next->random = cur->random->next; //则新拷贝结点的随机指针也指向原链表其他结点的后继结点 } cur = cur->next->next; //原链表按照自身顺序遍历 } -
新拷贝的结点已将数值域的值和随机指针域都成功拷贝,剩下的就是链接新链表和恢复原链表,将中间插入的拷贝结点与原链表分隔开来,成为两个结点数值和指向规律一模一样仅内存地址均不相同的两个独立链表,即完成了对于原链表的深拷贝:

深拷贝函数
RD* Copy(RD* Head) //将原随机链表深拷贝并返回首结点地址至实参
{
assert(Head);
RD* cur = Head;
while (cur) //第一层循环开辟待拷贝结点并中间插入到原链表中,并初步拷贝数值域和非随机域指针(next)
{
RD* copynode = BuyRandom(cur->data);
copynode->next = cur->next;
cur->next = copynode;
cur = copynode->next;
}
cur = Head;
while (cur) //拷贝随机域指针,其指向上一个原拷贝结点的随机指针指向的结点的下一个结点(即指向已拷贝的结点)
{
if (cur->random == NULL)
{
cur->next->random = NULL;
}
else if (cur->random == cur)
{
cur->next->random = cur->next;
}
else
{
cur->next->random = cur->random->next;
}
cur = cur->next->next;
}
cur = Head;
RD* copynode = cur->next;
RD* copyhead = copynode;
while (cur) //将深拷贝结点链接成链表,并将原链表恢复
{
cur->next = copynode->next;
cur = cur->next;
if (cur == NULL)
{
copynode->next = NULL;
break;
}
copynode->next = cur->next;
copynode = copynode->next;
}
return copyhead;
}
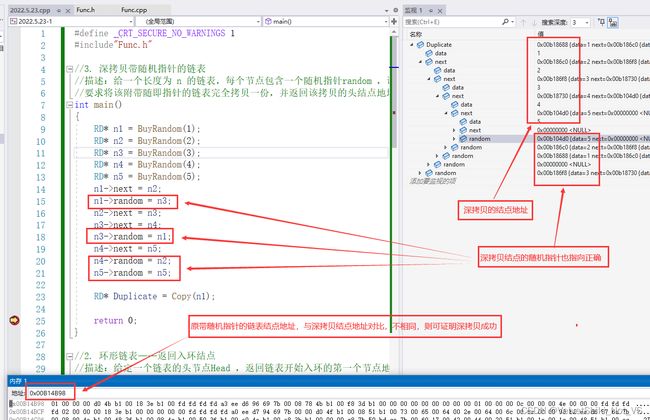
调用函数对上面给出的测试用例进行调试观察
RD* Duplicate = Copy(n1); //调试观察
通过调试观察到,新拷贝的链表头结点地址由Duplicate指向,且该新链表的所有结点值data,后继指向next和随机指针指向random都与原链表指向规律如出一辙,而内存占用地址完全不用,则可证明该新链表完成了对原链表的深拷贝。
⭐后话
- 博客项目代码开源,获取地址请点击本链接:CSDN-链表OJ2-环形-相交-分割等 · VelvetShiki_Not_VS。
- 若阅读中存在疑问或不同看法欢迎在博客下方或码云中留下评论。
- 欢迎访问我的Gitee码云,如果对您有所帮助还可以一键三连,获取更多学习资料请关注我,您的支持是我分享的动力~。