数据结构-----队列
数据结构之队列
数据结构的学习笔记,不妥之处请指正。文章目录
- 数据结构之队列
- 前言
- 一、先入先出的数据结构
-
- 1、先入先出的数据结构
- 2、队列的实现
- 3、循环队列
- 4、设计循环队列
- 二、队列和广度优先搜索
- 参考
前言
在数组中,可以通过索引访问 随机 元素。 但是某些情况下,可能需要限制处理的顺序。
下面我们将学习第一个 先入先出(FIFO) 的处理顺序,也就是队列。
一、先入先出的数据结构
1、先入先出的数据结构

在队列中,第一个进入的元素就是第一个被处理的元素(先进先出)。
队列有头有尾,我们平常所说的插入,在队列中叫做入队(Enqueue),入队发生在队列尾部(back),也就是说新元素始终会被添加在队列的尾部。删除在队列中被称为出队(Dequeue),而且出队发生在当前队列首部(front)。
2、队列的实现
队列支持两种操作:入队和出队。但是队列有头有尾,所以我们需要一个索引来指出头部。
class MyQueue {
// 队列
private List<Integer> data;
// 定义索引指向头部
private int p_start;
public MyQueue() {
data = new ArrayList<Integer>();
p_start = 0;
}
/** 入队成功则返回true */
public boolean enQueue(int x) {
data.add(x);
return true;
};
/** 出队成功则返回true */
public boolean deQueue() {
if (isEmpty() == true) {
return false;
}
data.remove(p_start);
p_start++;
return true;
}
/** 获取当前队列头部元素 */
public int Front() {
return data.get(p_start);
}
/** 判断当前队列是否为空 */
public boolean isEmpty() {
return p_start >= data.size();
}
};
public class Main {
public static void main(String[] args) {
MyQueue q = new MyQueue();
q.enQueue(666);
q.enQueue(999);
if (q.isEmpty() == false) {
System.out.println(q.Front());
}
q.deQueue();
if (q.isEmpty() == false) {
System.out.println(q.Front());
}
q.deQueue();
if (q.isEmpty() == false) {
System.out.println(q.Front());
}
}
}
实现很简单,但是在某些情况下效率很低。随着指针的移动,浪费了越来越多的空间,所以当我们的空间有限时是很难接受的。
如果我们只能分配一个最大长度为 5 的数组。当我们只添加少于 5 个元素时,我们的解决方案很有效。 例如,如果我们只调用入队函数四次后还想要将元素 10 入队,那么我们可以成功。

但是我们不能接受更多的入队请求,这是合理的,因为现在队列已经满了。但是如果我们将一个队列出队之后呢?
实际上在这种情况下,我们应该还能够再接受一个元素,但是索引的位置已经向后进行了移动,所以这就造成了空间浪费。

3、循环队列
上面所说的利用索引来进行队列的定位,是一种简单但是低效的方法,所以更为有效的方法是使用循环队列。
具体来说就是我们可以使用 固定大小的数组和两个指针来指示起始位置和结束位置。目的就是为了解决我们上面所提到的空间浪费。

由图可见,队列为空时,队首和队尾处于同一位置,并且队尾被连接在队首之后,形成一个循环。
当进行入队时,tail向后移动,当tail的next等于head时,说明当前队列已满。
当进行出队时,head向后移动,当head等于tail时,说明当前队列中仅存在一个元素,出队后,head和tail同时置为-1。
4、设计循环队列
难点:根据上述所说,循环队列最终为一个环形结构,我们可以利用一位数组模拟,通过操作索引构建一个虚拟环。
在循环队列中,我们使用一个数组和两个指针(head 和 tail)。 head 表示队列的起始位置,tail 表示队列的结束位置。
class MyCircularQueue {
private int[] data;
private int head;
private int tail;
private int size;
//构造方法
public MyCircularQueue(int k) {
this.data = new int [k];
this.head = -1;
this.tail = -1;
this.size = k ;
}
//入队
public boolean enQueue(int value) {
if(isFull()){
return false;
}
if(isEmpty()){
head = 0;
}
tail = (tail + 1) % size;//保证循环
data[tail] = value;
return true;
}
//出队
public boolean deQueue() {
if(isEmpty()){
return false;
}
if (head == tail) {
head = -1;
tail = -1;
return true;
}
head = (head + 1) % size;//保证循环
return true;
}
//获取队头元素
public int Front() {
if(isEmpty()){
return -1;
}
return data[head];
}
//获取队尾元素
public int Rear() {
if(isEmpty()){
return -1;
}
return data[tail];
}
//判队列是否为空
public boolean isEmpty() {
return head == -1;
}
//判断队列是否已满
public boolean isFull() {
return ((tail + 1) % size) == head;
}
}
其实大多数流行语言都提供了内置的队列库,所以我们没有必要自己创建。只需要记住队列有两个重要的操作:入队和出队。另外,我们还应该可以获取到当前队列的第一个元素,因为我们首先要处理的就是它。
所以当你想到需要用顺序处理数据时,请记住队列这个选择。
二、队列和广度优先搜索
先决条件:树的层序遍历
广度优先搜索(BFS是一种遍历或搜索数据结构(如数或图)的算法。我们可以使用BFS在树中执行层序遍历,也可以使用BFS遍历图。
例如,我们可以使用BFS找到从起始点到目标结点的路径,特别是最短路径。
广度优先搜索(BFS)的一个常见应用是找出从根节点到目标结点的最短路径。
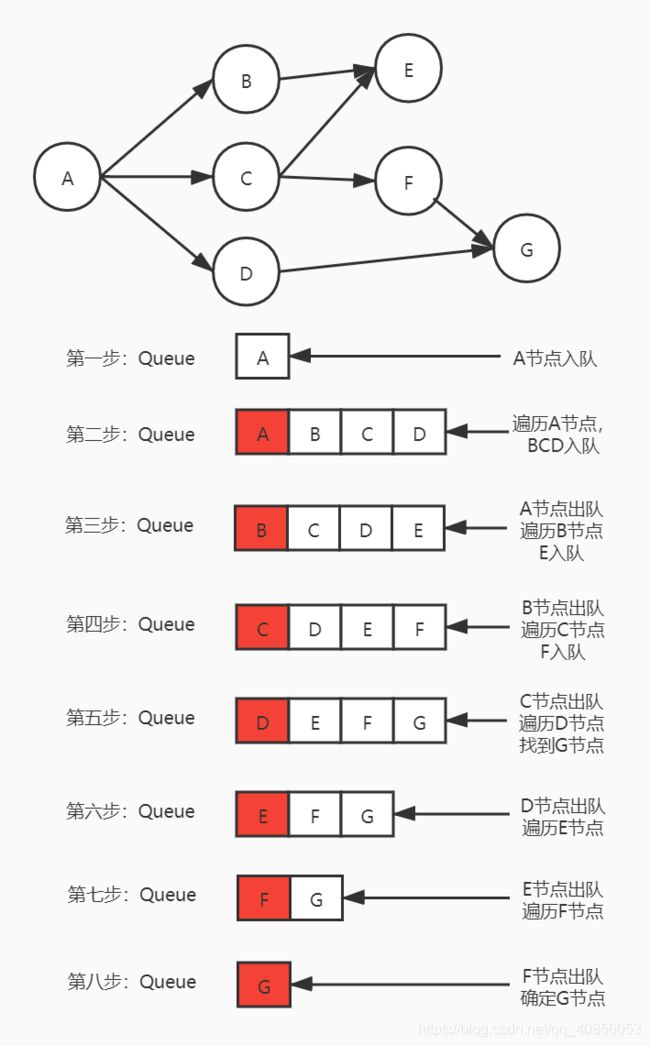
结点的处理顺序
在第一步中,我们处理根结点。在第二步中,我们处理根结点旁边的结点;在第三步中,我们处理距根结点两步的结点;等等等等。
与树的层序遍历类似,越是接近根结点的结点将越早地遍历。
如果在第 k 轮中将结点 X 添加到队列中,则根结点与 X 之间的最短路径的长度恰好是 k。也就是说,第一次找到目标结点时,你已经处于最短路径中。
队列的入队和出队顺序
我们首先将根结点排入队列。然后在每一轮中,我们逐个处理已经在队列中的结点,并将所有邻居添加到队列中。值得注意的是,新添加的节点不会立即遍历,而是在下一轮中处理。
结点的处理顺序与它们添加到队列的顺序是完全相同的顺序,即先进先出(FIFO)。这就是我们在 BFS 中使用队列的原因。
广度优先搜索-模板
/**
* 返回根结点到目标结点的最短路径
*/
int BFS(Node root, Node target) {
Queue<Node> queue;
int step = 0;
// 初始化
add root to queue;
// BFS
while (queue is not empty) {
step = step + 1;
// 遍历根结点
int size = queue.size();
for (int i = 0; i < size; ++i) {
Node cur = the first node in queue;
return step; //当前节点若是目标结点则返回
for (Node next : the neighbors of cur) {
//入队,添加下一结点;
}
//出队,移除队首;
}
}
return -1; //无最短路径返回-1
}
如代码所示,在每一轮中,队列中的结点是等待处理的结点。
在每个更外一层的 while 循环之后,我们距离根结点更远一步。变量 step 指示从根结点到我们正在访问的当前结点的距离。
参考
https://www.cnblogs.com/jamaler/p/11437217.html
https://leetcode-cn.com/leetbook/read/queue-stack/kkqf1/