数据结构之图的应用(二)之最短路径
前面我们一期文章我们分享了图的应用中的一种——最小生成树。现在我们开始来讲讲第二种——最短路径。最短路径问题在我们日常生活中也是很常见的。比如我们从一个地点要去另一个地点玩,路径可以有千千万万条,但我们要选择出最短路径来节省时间或者金钱等等。在我们算法学习中,最短路径问题也有涉及到几个算法。主要是两个经典算法——Dijkstra迪杰斯特拉算法和Floyd弗罗伊德算法。下面让我们一起来看看吧。
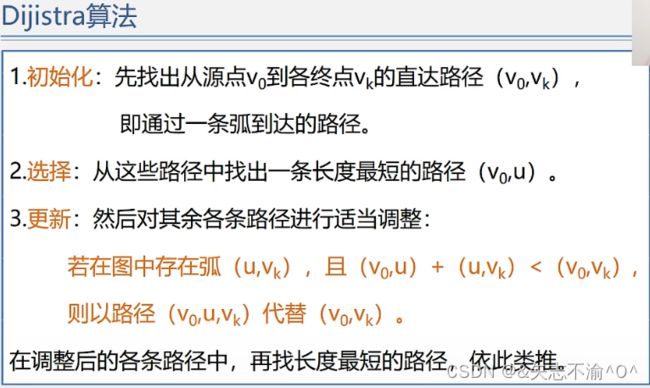
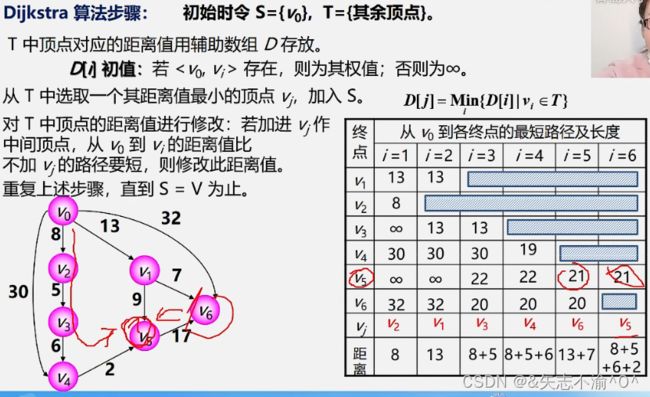
一.单源最短路径——Dijkstra迪杰斯特拉算法(主要用于求解某一个顶点到达全部顶点的最短路径)
核心思路:
//邻接矩阵
#include
#define MAXSIZE 100
#define INFINITY 65535 //表示无边(Weight有时为0,不用0表示)
typedef char VertexType;
typedef int EdgeType;
typedef struct
{
VertexType vexs[MAXSIZE]; //顶点表
EdgeType arc[MAXSIZE][MAXSIZE]; //邻接矩阵
int numVertexes, numEdges; //顶点数和边数
}MGraph;
void CreateMGraph(MGraph* G)
{
int i, j, k, w;
printf("输入顶点数和边数:\n");
scanf("%d%d", &G->numVertexes, &G->numEdges);
for (i = 0; i < G->numVertexes; i++)
scanf("%c", &G->vexs[i]);
//初始化邻接矩阵
for (i = 0; i < G->numVertexes; i++)
for (j = 0; j < G->numVertexes; j++)
G->arc[i][j] = INFINITY;
for (k = 0; k < G->numEdges; k++)
{
printf("输入边(vi, vj)的下标i和上标j和权w:\n");
scanf("%d%d%d", &i, &j, &w);
G->arc[i][j] = w;
G->arc[j][i] = G->arc[i][j]; //无向图矩阵对称
}
}
//迪杰斯特拉算法生成最短路径
//求解有向网G的v0顶点到其余顶点v最短路径P[v]及带权长度D[v]
//P[v]:前驱下标顶点,D[v]:v0到v的最短路径长度
#define MAXVEX 9
typedef int Patharc[MAXVEX]; //存储最短路径下标
typedef int ShortPathTable[MAXVEX]; //最短路径权值和
void Dijkstra(MGraph G, int v0, Patharc* P, ShortPathTable* D)//整个算法核心部分
{
int v, w, k, min;
int final[MAXVEX]; //final[w]=1表示求得v0至vw最短路径
//初始化数据
for (v = 0; v < G.numVertexes; v++)
{
final[v] = 0;
(*D)[v] = G.arc[v0][v]; //将与v0有连线的顶点加上权值。邻接矩阵
(*P)[v] = 0;
}
(*D)[v0] = 0;
final[v0] = 1;
//每次求得v0到某个顶点的最短路径
for (v = 1; v < G.numVertexes; v++)
{
min = INFINITY; //无穷大值
//找到当前离v0最近的点(未求得最短路径的),用k记录其下标
for (w = 0; w < G.numVertexes; w++)
{
if (!final[w] && (*D)[w] < min)
{
k = w;
min = (*D)[w];
}
}
final[k] = 1;
//修正邻接点当前最短路径及距离
for (w = 0; w < G.numVertexes; w++)
{
//若以w为前驱顶点的路径更短,更新路径和放有前驱顶点的数组P[v]
if (!final[w] && (min + G.arc[k][w] < (*D)[w]))
{
(*D)[w] = min + G.arc[k][w];
(*P)[w] = k;
}
}
}
}
2.所有顶点间的最短路径——Floyd弗罗伊德算法
核心思路:
主要步骤:
求图中任意顶点vi到vj的最短路径。
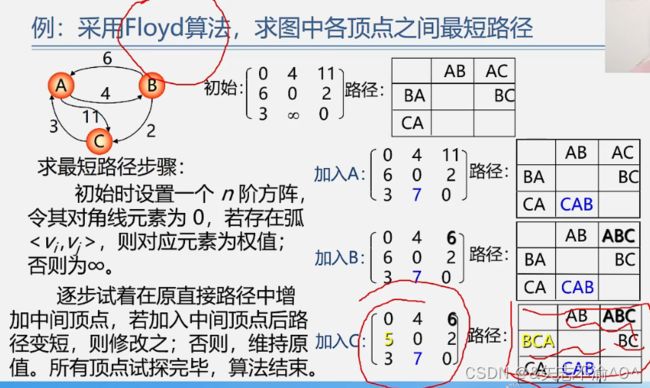
① 将vi到vj的最短路径长度初始化为对应邻接矩阵G.arcs[i][j]值,然后进行如下n次比较和修正:
② 在vi和vj间加入顶点v0,比较(vi,v0,vj)和(vi,vj)的路径长度,取较短的路径作为vi到vj的当前最短路径,如此类推依次加入v1、v2…经过n次比较和修正,得到vi到vj的最短路径。
具体参考下图例子:
完整代码:
/*图的最短路径——Floyd算法*/
# include
# define MAX_VERTEX_NUM 20 //最多顶点个数
# define INFINITY 32768
/*图的邻接矩阵表示法*/
typedef int AdjType;
typedef char VertexData;
typedef struct ArcNode
{
AdjType adj; //无权图用1或0表示是否相邻,带权图则为权值类型
}ArcNode;
typedef struct
{
VertexData vertex[MAX_VERTEX_NUM]; //顶点向量
ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邻接矩阵
int vexnum, arcnum; //图的顶点数和弧数
}AdjMatrix;
/*采用邻接矩阵表示法创建有向网*/
/*求顶点位置*/
int LocateVertex(AdjMatrix* G, VertexData v) {
int k;
for (k = 0; k < G->vexnum; k++) {
if (G->vertex[k] == v)
break;
}
return k;
}
/*创建有向网*/
int CreateDN(AdjMatrix* G) {
int i, j, k, weight;
VertexData v1, v2;
printf("输入图的顶点数和弧数:"); //输入图的顶点数和弧数
scanf("%d%d", &G->vexnum, &G->arcnum);
for (i = 0; i < G->vexnum; i++) { //初始化邻接矩阵
for (j = 0; j < G->vexnum; j++)
G->arcs[i][j].adj = INFINITY;
}
printf("输入图的顶点:");
for (i = 0; i < G->vexnum; i++) //输入图的顶点
scanf(" %c", &G->vertex[i]);
for (k = 0; k < G->arcnum; k++) {
printf("输入第%d条弧的两个顶点及权值:", k + 1);
scanf(" %c %c %d", &v1, &v2, &weight); //输入一条弧的两个顶点及权值
i = LocateVertex(G, v1);
j = LocateVertex(G, v2);
G->arcs[i][j].adj = weight; //建立弧
}
}
/*顶点集合,用于存放顶点和路径*/
typedef struct {
char elem[MAX_VERTEX_NUM];
int last;
}PathSet[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
PathSet path; //path[i][j]中存放vi到vj的当前最短路径
/*路径集合初始化*/
void InitPathSet(PathSet path, int i, int j) {
path[i][j].last = -1;
}
/*路径集合添加操作*/
void AddPath(PathSet path, int i, int j, char c) {
path[i][j].last++;
path[i][j].elem[path[i][j].last] = c;
}
/*两个路径集合path[i][k]和path[k][j]合并操作*/
void Join(PathSet path, int i, int j, int k) {
int t;
for (t = 0; t <= path[i][k].last; t++)
path[i][j].elem[t] = path[i][k].elem[t];
for (t = path[i][k].last + 1; t <= path[i][k].last + path[k][j].last; t++)
path[i][j].elem[t] = path[k][j].elem[t - path[i][k].last];
path[i][j].last = path[i][k].last + path[k][j].last;
}
int dist[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //dist[i][j]为vi到vj的当前最短路径长度
/*Floyd算法*/
void ShortestPath_DJS(AdjMatrix G) {
int i, j, k;
for (i = 0; i < G.vexnum; i++) { //初始化dist[i][j]和path[i][j]
for (j = 0; j < G.vexnum; j++) {
InitPathSet(path, i, j);
dist[i][j] = G.arcs[i][j].adj;
if (dist[i][j] < INFINITY) {
AddPath(path, i, j, G.vertex[i]);//若vi和vj之间有路径,则将该路径添加到对应的path[i][j]中
AddPath(path, i, j, G.vertex[j]);
}
}
}
for (k = 0; k < G.vexnum; k++) {
for (i = 0; i < G.vexnum; i++) {
for (j = 0; j < G.vexnum; j++) {
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
Join(path, i, j, k); //两个路径集合path[i][k]和path[k][j]合并
}
}
}
}
}
int main() {
int i, j, k;
AdjMatrix G;
CreateDN(&G);
ShortestPath_DJS(G);
printf("\n");
for (i = 0; i < G.vexnum; i++) {
for (j = 0; j < G.vexnum; j++) {
if (i != j) {
printf("v%c->v%c的最短路径:", G.vertex[i], G.vertex[j]);
if (dist[i][j] < INFINITY) {
for (k = 0; k <= path[i][j].last; k++)
printf("v%c ", path[i][j].elem[k]);
printf("\t路径长度为:%d", dist[i][j]);
printf("\n");
}
else
printf("无法到达!\n");
}
}
}
return 0;
}
好啦,关于图的应用之最短路径的两种算法就分享到这啦,我们有空的时候多想想原理,多理解理解。以后刷算法题时也是有可能遇到的。
本贴为博主亲手整理。如有错误,请评论区指出,一起进步。谢谢大家的浏览.