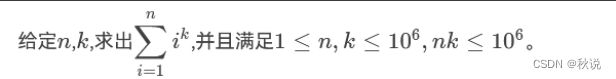【C语言必知必会 | 子系列第六篇】深入剖析循环结构（2）

引言

C语言是一门面向过程的、抽象化的通用程序设计语言，广泛应用于底层开发。它在编程语言中具有举足轻重的地位。
此文为【C语言必知必会】第六篇，基于进行C语言循环结构的编程题专项练习，结合专题优质题目，带领读者从0开始，深度掌握知识点。

---

1️⃣ 前言

在【C语言必知必会】系列中，我们学习了顺序结构、选择结构、循环结构等，同时也通过专项练习进行了知识点的巩固和手敲代码的锻炼。

在子系列中，我们将基于PTA教学平台，向C语言学习者提供更优质的题目与更巧妙、精髓的解题思想与方法。

PTA是一个程序设计类实验辅助教学平台,由千名老师共同建设,里面包含了上万道高质量题目,用户量达百万。

在本讲中，将深入讲解循环结构编程题，在思想上引领读者，带领读者在理论结合实际的基础上更好地学习、吸收、掌握C语言。

---

2️⃣PTA专项练习

接下来，开始我们的循环结构专篇练习。

7-1 统计一行字符中各类字符的个数

用户输入一行字符（以回车符作为结束），请统计这行字符中，大小写字母个数、数字字符个数、空格个数和其它字符个数。

输入格式:
一行字符，以回车符作为结束。

输出格式:
输出4个以空格作为间隔的整数，分别代表大小写字母个数、数字字符个数、空格个数和其它字符的个数。

输入样例:

Tersfi23&* sdf   A$

输出样例:

10 2 4 3

解题思路：

使用while语句结合getchar函数来匹配回车符

代码如下：

#include 
int main()
{
	int zimu=0,shuzi=0,space=0,other=0;
	char c;
	while((c=getchar())!='\n')
	{
		if((c>='a'&&c<='z')||(c>='A'&&c<='Z'))
		{
			zimu++;
		}
		
	else	if(c>='0'&&c<='9')
		{
			shuzi++;
		}
		
	else	if(c==' ')
		{
			space++;
		}
		
	else{
		other++;
	}
	}
	
	printf("%d %d %d %d",zimu,shuzi,space,other);
	
}

---

7-2 打印九九口诀表

下面是一个完整的下三角九九口诀表：

1*1=1   
1*2=2   2*2=4   
1*3=3   2*3=6   3*3=9   
1*4=4   2*4=8   3*4=12  4*4=16  
1*5=5   2*5=10  3*5=15  4*5=20  5*5=25  
1*6=6   2*6=12  3*6=18  4*6=24  5*6=30  6*6=36  
1*7=7   2*7=14  3*7=21  4*7=28  5*7=35  6*7=42  7*7=49  
1*8=8   2*8=16  3*8=24  4*8=32  5*8=40  6*8=48  7*8=56  8*8=64  
1*9=9   2*9=18  3*9=27  4*9=36  5*9=45  6*9=54  7*9=63  8*9=72  9*9=81  

本题要求对任意给定的一位正整数N，输出从1*1到N*N的部分口诀表。

输入格式：
输入在一行中给出一个正整数N（1≤N≤9）。

输出格式：
输出下三角N*N部分口诀表，其中等号右边数字占4位、左对齐。

输入样例：

4

输出样例：

1*1=1   
1*2=2   2*2=4   
1*3=3   2*3=6   3*3=9   
1*4=4   2*4=8   3*4=12  4*4=16  

解题思路：

• 使用for循环嵌套

• 当两个乘数相等时换行

代码如下：

#include 
int main()
{
	int i,j;
	int n;
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=i;j++)
		{
			printf("%d*%d=%4d",j,i,j*i);
			if(i==j)
			{
				printf("\n");
			}
		}
	}
}

注意：

- 表示左对齐，而 4 表示占据4位宽度

右对齐直接%4d就行

---

7-3 二分法求多项式单根

二分法求函数根的原理为：如果连续函数f(x)在区间[a,b]的两个端点取值异号，即f(a)f(b)<0，则它在这个区间内至少存在1个根r，即f®=0。

二分法的步骤为：

• 检查区间长度，如果小于给定阈值，则停止，输出区间中点(a+b)/2；否则
• 如果f(a)f(b)<0，则计算中点的值f((a+b)/2)；
• 如果f((a+b)/2)正好为0，则(a+b)/2就是要求的根；否则
• 如果f((a+b)/2)与f(a)同号，则说明根在区间[(a+b)/2,b]，令a=(a+b)/2，重复循环；
• 如果f((a+b)/2)与f(b)同号，则说明根在区间[a,(a+b)/2]，令b=(a+b)/2，重复循环。

本题目要求编写程序，计算给定3阶多项式f(x)=a3*x^3+a2*x^2+a1*x+a0在给定区间[a,b]内的根。

输入格式：
输入在第1行中顺序给出多项式的4个系数a3、a2、a1、a0，在第2行中顺序给出区间端点a和b。题目保证多项式在给定区间内存在唯一单根。

输出格式：
在一行中输出该多项式在该区间内的根，精确到小数点后2位。

输入样例：

3 -1 -3 1
-0.5 0.5

输出样例：

0.33

解题思路：

按照题目要求构建代码即可

代码如下：

#include
 
int main()
{
	double a0,a1,a2,a3,a,b;
	scanf("%lf %lf %lf %lf %lf %lf",&a3,&a2,&a1,&a0,&a,&b);
	while((b-a)>0.01)
	{
		
		double s=(a+b)/2;
		double fs=a3*s*s*s+a2*s*s+a1*s+a0;
		double fa=a3*a*a*a+a2*a*a+a1*a+a0;
		double fb=a3*b*b*b+a2*b*b+a1*b+a0;
		if(fs==0){
			printf("%lf",s);
		}
		if(fa*fb<=0)
		{
		if(fs/fa>0)
			a=s;
		else
			b=s;
		}

	}
	printf("%.2lf",(a+b)/2);
	
	return 0;
} 

---

7-4 梅森数

形如2n−1的素数称为梅森数（Mersenne Number）。例如22−1=3、23−1=7都是梅森数。1722年，双目失明的瑞士数学大师欧拉证明了2^31−1=2147483647是一个素数，堪称当时世界上“已知最大素数”的一个记录。

本题要求编写程序，对任一正整数n（n<20），输出所有不超过2n−1的梅森数。

输入格式：
输入在一行中给出正整数n（n<20）。

输出格式：
按从小到大的顺序输出所有不超过2n−1的梅森数，每行一个。如果完全没有，则输出“None”。

输入样例：

6

输出样例：

3
7
31

解题思路：

先满足2^n-1的形式，再计算是否为素数

代码如下：

#include 
#include 
int main()
{
	int n,i,c,j,ge=0;
	scanf("%d",&n);
	for(i=2;i<=n;i++)   //满足梅森数的形式
	{
		c=pow(2,i)-1;
		
		for(j=2;j<=c-1;j++)
		{
			if(c%j==0)
			{
				break;  //不是素数
			}
			
		}
		if(j>c-1) //是素数的条件
		{
			printf("%d\n",c);  
			ge++;
		}
		
	}
	if(ge==0)
	{
		printf("None");
	}
}

---

7-5 单词长度

你的程序要读入一行文本，其中以空格分隔为若干个单词，以.结束。你要输出每个单词的长度。这里的单词与语言无关，可以包括各种符号，比如it's算一个单词，长度为4。注意，行中可能出现连续的空格；最后的.不计算在内。

输入格式：
输入在一行中给出一行文本，以.结束

提示： 用scanf("%c",...);来读入一个字符，直到读到.为止。

输出格式：
在一行中输出这行文本对应的单词的长度，每个长度之间以空格隔开，行末没有最后的空格。

输入样例：

It's great to see you here.

输出样例：

4 5 2 3 3 4

解题思路：

使用循环读取字符，直到读取到 . 字符或者无法继续读取为止。

在循环中，判断当前读取的字符是否为空格。如果是空格，则说明一个单词的长度统计完成，需要输出该单词的长度，并将 wordCount 加一，wordLength 归零。

如果当前字符不是空格，则说明当前字符属于一个单词内部，将 wordLength 加一以统计单词的长度。

循环结束后，需要处理最后一个单词。如果 wordLength 大于0，说明最后一个单词的长度统计完成，需要输出该单词的长度，并将 wordCount 加一。

代码如下：

#include 

int main() {
    char ch;
    int wordCount = 0; // 单词计数器
    int wordLength = 0; // 当前单词长度

    while (scanf("%c", &ch) == 1 && ch != '.') {
        if (ch == ' ') {
            if (wordLength > 0) {
                printf("%d ", wordLength);
                wordCount++;
                wordLength = 0;
            }
        } else {
            wordLength++;
        }
    }

    // 输出最后一个单词的长度
    if (wordLength > 0) {
        printf("%d", wordLength);
        wordCount++;
    }

    printf("\n");
    
    return 0;
}

---

7-6 21循环-求和3

sxtc爱做数学题，今天他又拿到一道数学题：

注意答案有可能很大，请对114514取模。

他希望擅长求和的你帮他解出这个求和问题。

输入格式:
读入两个数n,k。

输出格式:
输出求和结果，请对答案取模114514。

输入样例:
在这里给出一组输入。例如：

11451 4

输出样例:
在这里给出相应的输出。例如：

113968

解题思路：
使用两个嵌套的 for 循环来计算积和求和。外层循环控制变量 i 从1到 n，内层循环控制变量 e 从1到 k。在每次内层循环中，通过 d = (d * c) % 114514 实现了累乘的操作，并将结果存储在变量 d 中。

在外层循环的每次迭代结束后，将 d 累加到变量 f 中，并在累加之前通过 % 114514 运算符对 d 进行取模操作。最后，通过 % 114514 运算符对 f 进行取模操作，并输出结果。

代码如下：

#include 

int main() {
    int n, k;
    scanf("%d%d", &n, &k);

    int d = 1;
    int f = 0;

    for (int i = 1; i <= n; i++) {
        for (int e = 1; e <= k; e++) {
            d = (d * i) % 114514;
        }
        f = (f + d) % 114514;
        d = 1;
    }

    printf("%d", f);
    return 0;
}

---

7-7 21循环-金字塔

SeraphJACK正在摆积木。他想用这些积木垒成一座金字塔。同时摆好金字塔之后，他为每层积木涂上不同的颜色，这些颜色用从1开始的正整数表示，从最底层开始涂色。现在告诉你SeraphJACK有n块积木，请输出他用这些积木能摆出并涂色的最大金字塔。（金字塔形状详见样例,0表示这个位置没有积木）

输入格式:
一个整数n,1<=n<=1000

输出格式:
涂色后的金字塔

输入样例1:
在这里给出一组输入。例如：

11

输出样例1:
在这里给出相应的输出。例如：

0004000
0030300
0202020
1010101

输入样例2:
在这里给出一组输入。例如：

1

输出样例2:
在这里给出相应的输出。例如：

1

解题思路：

外层使用 for 循环，用于确定金字塔的层数。通过不断增加 b（层数） 的值，直到满足积木数量 b * (b + 1) / 2 大于或等于输入的积木数量 a。

内层嵌套使用两个 while 循环，用于打印每一层的积木。其中，第一个 while 循环控制层数，从第一层开始到倒数第二层。第二个 while 循环控制打印每一层的积木个数和颜色。

在第二个 while 循环中，根据打印位置的关系来判断是否打印积木和积木的颜色。若当前位置在金字塔的边缘或超出边缘范围，则打印0；否则，根据 (d-b+1+c)%2==1 的条件判断来决定打印的颜色。

代码如下：

#include
int main()
{
    int a,b,c=1,d;
    scanf("%d",&a);
    for(b=1;b*(b+1)/2<=a;b++);
    while(c<=(b-1))
    {
        d=1;
        while(d<=2*b-3)
        {
            if(d<=(b-1-c)||d>b-2+c)
                printf("0");
            else if((d-b+1+c)%2==1)
                printf("%d",b-c);
            else printf("0");
            d++;
        }
        printf("\n");
        c++;
    }
    return 0;
}

---

3️⃣ 总结

此文为 【C语言必知必会】子系列第六篇 ，通过以题代练的形式带领读者掌握C语言的循环结构，带领读者从0开始，深度掌握知识点。

以题代练对于C语言的学习是十分重要的，专栏将持续提供优质C语言编程题与理论课的学习，带领读者全方位掌握C语言。读者可订阅专栏持续跟进。