R语言-随机前沿分析法--SFA

    3.1介绍

生产函数模型：   lnqi=x’i*b+vi-ui                  （随机生产前沿函数）

qi：产出变量向量

x’i：投入变量向量

b：变量参数估计

vi:统计噪声的对称随机误差

ui:无效效应

3.2度量技术效率的方法—SFA（参数），DEA（非参数）

在经济学中，技术效率是指在既定的投入下产出可增加的能力或在既定的产出下投入可减少的能力。常用度量技术效率的方法是生产前沿分析方法。

所谓生产前沿是指在一定的技术水平下，各种比例投入所对应的最大产出集合。

而生产前沿通常用生产函数表示。

前沿分析方法根据是否已知生产函数的具体的形式分为参数方法和非参数方法，前者以随机前沿分析为代表，后者以数据包络分析为代表。

3.3 SFA

SFA是前沿分析中参数方法的典型代表，即需要确定生产前沿的具体形式。与非参数方法相比，它的最大优点是考虑了随机因素对于产出的影响。

SFA要解决的问题是要度量n个决策单元T期的技术效率（TE），每个决策单元都是m种投入和一种产出。

随机前沿生产函数在确定性生产函数的基础上提出了具有复合扰动项的随机边界模型。其主要思想为随机扰动项ε应由v 和u 组成。

v 是随机误差项, 是企业不能控制的影响因素, 具有随机性, 用以计算系统非效率;

u是技术损失误差项, 是企业可以控制的影响因素, 可用来计算技术非效率。

很明显, 参数型随机前沿生产函数体现了样本的统计特性, 也反映了样本计算的真实性。

3.4对生产率进行拆分 的两种 前沿生产函数模型

	指数方法	DEA	SF
是否为参数方法	非参数方法	非参数方法	参数方法
是否考虑随机影响	否	否	是
关于公司效率假设	不存在无效率	存在无效率	存在无效率
行为假设	成本最小 收益最大	无（考虑配置效率时除外）	无
可计算哪些方面	TFP的变化	技术效率、规模效率、配置效率	技术效率、规模效率、配置效率、技术进步、TFP的变化
所需要变量	投入产出的数量和价格	投入产出的数量	投入产出的数量
所需要数据	时间序列、截面数据、面板数据	截面数据 面板数据	截面数据 面板数据

DEA是一种非参数方法，它不设定具体的函数形式，也就是说DEA的分析中，没有生产函数这一概念，但是有生产边界的概念。其实严格来说，在DEA中，（技术）效率指的就是现实中的某厂商的生产率跟处于生产边界上的厂商的生产率之比值。生产边界是通过数学规划（一般是线性规划）的手段来寻找，用DEA可解出处在生产边界上的厂商，其技术效率值即为1,其他厂商都跟它去比。

而SFA则是一种参数方法，需要设定生产函数的函数形式，并利用一种特别的SFA回归方法，估计出生产函数。SFA下的技术效率，严格地说，是现实中的某厂商的生产率与估计出的生产函数上的“虚拟厂商”的生产率之比值。技术效率最高的厂商未必处于生产函数之上。

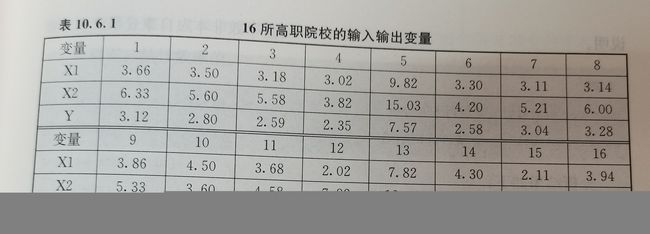
3.5 例：高职院校办学效益评价研究

#下载及加载安装包

install.packages("Benchmarking")             #下载及安装"Benchmarking"包

library(lpSolveAPI)                                  #载入"lpSolveAPI"包

library(ucminf)                                      #载入" ucminf"包

library(Benchmarking)                             #载入"Benchmarking"包

 

 

#整理原始数据并输入R程序

n <- 16                           

#设定样本笔数

x1 <- c(3.66, 3.50, 3.18, 3.02, 9.82, 3.30, 3.11, 3.14, 3.86, 4.50, 3.68, 2.02, 7.82, 4.30, 2.11, 3.94)

x2 <- c(6.33, 5.60, 5.58, 3.82, 15.03, 4.20, 5.21, 6.00, 5.33, 3.60, 4.58, 7.82, 12.03, 5.20, 2.21, 3.00)

x <- cbind(x1,x2)

y <- 0.5+ 1.5*x1 + 2.5*x2 + 1.5*log(x1)^2 + 2*log(x2)^2 + 2.5*log(x1)*log(x2) + rnorm(n,0,1) - pmax(0,rnorm(n,0,1))

#Translog

#执行SFA

output <- sfa(x,y)                            #运行SFA分析

summary(output)                          #统计分析结果

#percentage of inefficiency variation (u) to total variation

#计算成本非效率差占总误差的百分比

#成本非效率差(u), 随机误差(v)

lambda<-lambda.sfa(output)

100*lambda^2/(1+lambda^2)        #计算成本非效率差(u)占总误差百分比

 分析：成本非效率差sigma2u占总误差的99.99999%，更说明了无效效应大部分来自成本非效率差。

# 估计三种效率值te, teM及teJ

eff(output)

te <- te.sfa(output)

teM <- teMode.sfa(output)

teJ <- teJ.sfa(output)

cbind(te,teM,teJ)[1:16,]                     #数字16为16间学校(DMU)