leetcode51. N 皇后|C++|回溯|递归

题目链接：力扣

题目描述

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

 输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。
示例 2：

输入：n = 1
输出：[["Q"]]
 

提示：

1 <= n <= 9

果果念

又是很久没有刷题了，手感变陌生了，最快下周就要面试了，加油。

这是很经典的N皇后问题，调研的资料显示最优复杂度也是O(N!)，因此和全排列差不多。回溯的话，找到边界条件；另外，要明白八皇后的规则。

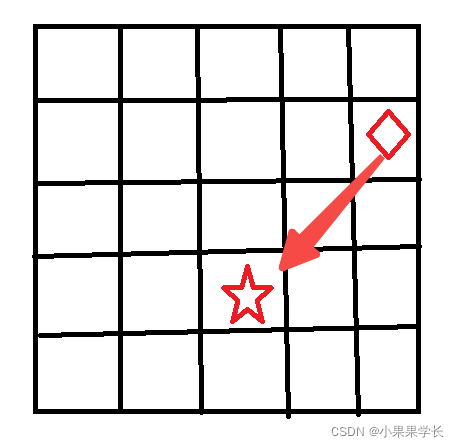
皇后会在同一行或者同一列进行攻击，值得一提的是，他们也会在斜线上进行攻击，并不是简单的对角线的前后两行，而是很长的斜线上。这一点刚开始做的时候没有考虑到，导致出的结果不正确。即下图中的排列也是不行的，因为他们在同一条斜线上。

说一下具体的思路：可以按行或者按列进行检索，利用一个数组存储不同的位置。我使用的是一个path记录每次排放的各行的列下标，num指的是每一行。最后返回答案的时候，换成字符串即可。

 

 代码

这个代码算法复杂度是，O(N)是判断对角线的，当然，这个可以用一个数组保存对角线的位置，进行标记，就像标记列一样，不过需要两个对角线数组，你知道为什么吗？因为左右对角线不同呀。这个在代码2中有，是我参考的一个大佬写的。膜拜。

class Solution {
    //不可以同行、同列、对角线
public:
    vector> pathSum;
    vector book;//标记数组，此列是否标记

    vector> solveNQueens(int n) {
        
        for(int i=0;i path;
        getPath(0,n,path);

        vector> pathAns;
        
        string a;
        for(int i=0;i stringRow;
            for(int j=0;j& path){
        if(num==n){

            pathSum.push_back(path);
     
            return;
        }
        
        for(int i=0;i=0;j--,index++){
                    //判断是否在斜线上
                    if(path[j]==i-index||path[j]==i+index){
                        flag=true;
                        break;
                    }
                }
                if(flag==false){
                    path.push_back(i);
                    book[i]=1;
                    getPath(num+1,n,path);
                    path.pop_back();
                    book[i]=0;
                }
                }
            }

    }
};

对角线优化

刚刚看了一个题解，博主对角线也记录了下来，这样就少了一个循环。算法复杂度O(N!)。

class Solution {
        public List> solveNQueens(int n) {
            char[][] grid = new char[n][n];         // n * n 的棋盘
            boolean[] col = new boolean[n];         //列
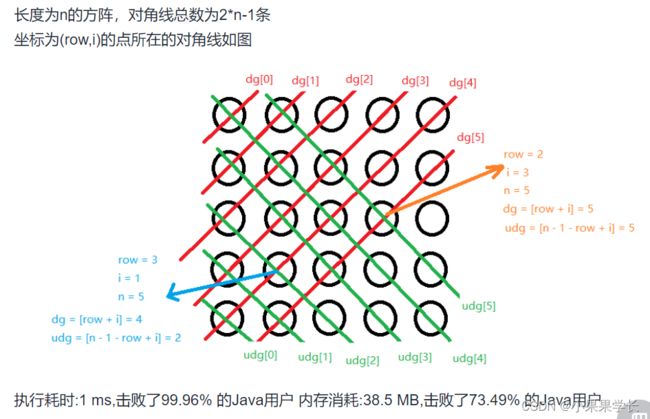
            boolean[] dg = new boolean[2 * n - 1];  //对角线（右上到左下的对角线，dg[0]为左上角grid[0][0]的元素，dg[1]为grid[0][1]和gird[1][0]，...）
            boolean[] udg = new boolean[2 * n - 1]; //反对角线（左上到右下的对角线，udg[0]为左下角grid[n-1][0]的元素，ud1[1]为grid[n-2][0]和gird[n-1][1]，...）

            for (int i = 0; i < n; i++) {           //初始化棋盘
                for (int j = 0; j < n; j++) {
                    grid[i][j] = '.';
                }
            }

            List> lists = new ArrayList<>();
            List list = new ArrayList<>();
            dfs(0, n, grid, col, dg, udg, lists, list);
            return lists;
        }

        private void dfs(int row, int n, char[][] grid, boolean[] col, boolean[] dg, boolean[] udg, List> lists, List list) {
            if (row == n) { //递归到最后一行
                for (int i = 0; i < n; i++) {
                    list.add(new String(grid[i]));  //全部排列完毕、将第i行添加进结果(list)中
                }
                lists.add(new ArrayList<>(list));   //将当前结果list添加进结果集(lists)中
                list.clear();
            } else {
                //当前在第row行，从第0列到n-1列进行循环
                for (int i = 0; i < n; i++) {
                    //当前列、对角线、反对角线有元素则跳过（剪枝）
                    if (col[i] || dg[i + row] || udg[i + n - 1 - row]) {
                        continue;
                    }
                    //当前位置（row = row,col = i）可用
                    grid[row][i] = 'Q';
                    //当前列和对角线设置为ture，即已经用过
                    col[i] = dg[i + row] = udg[i - row + n - 1] = true;
                    //递归进下一行
                    dfs(row + 1, n, grid, col, dg, udg,lists,list);
                    //回溯
                    grid[row][i] = '.';
                    col[i] = dg[i + row] = udg[i - row + n - 1] = false;
                }
            }
        }
    }

作者：Alkaidling
链接：https://leetcode-cn.com/problems/n-queens/solution/nhuang-hou-bu-yong-ha-xi-biao-shi-yong-b-d2vj/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。class Solution {
        public List> solveNQueens(int n) {
            char[][] grid = new char[n][n];         // n * n 的棋盘
            boolean[] col = new boolean[n];         //列
            boolean[] dg = new boolean[2 * n - 1];  //对角线（右上到左下的对角线，dg[0]为左上角grid[0][0]的元素，dg[1]为grid[0][1]和gird[1][0]，...）
            boolean[] udg = new boolean[2 * n - 1]; //反对角线（左上到右下的对角线，udg[0]为左下角grid[n-1][0]的元素，ud1[1]为grid[n-2][0]和gird[n-1][1]，...）

            for (int i = 0; i < n; i++) {           //初始化棋盘
                for (int j = 0; j < n; j++) {
                    grid[i][j] = '.';
                }
            }

            List> lists = new ArrayList<>();
            List list = new ArrayList<>();
            dfs(0, n, grid, col, dg, udg, lists, list);
            return lists;
        }

        private void dfs(int row, int n, char[][] grid, boolean[] col, boolean[] dg, boolean[] udg, List> lists, List list) {
            if (row == n) { //递归到最后一行
                for (int i = 0; i < n; i++) {
                    list.add(new String(grid[i]));  //全部排列完毕、将第i行添加进结果(list)中
                }
                lists.add(new ArrayList<>(list));   //将当前结果list添加进结果集(lists)中
                list.clear();
            } else {
                //当前在第row行，从第0列到n-1列进行循环
                for (int i = 0; i < n; i++) {
                    //当前列、对角线、反对角线有元素则跳过（剪枝）
                    if (col[i] || dg[i + row] || udg[i + n - 1 - row]) {
                        continue;
                    }
                    //当前位置（row = row,col = i）可用
                    grid[row][i] = 'Q';
                    //当前列和对角线设置为ture，即已经用过
                    col[i] = dg[i + row] = udg[i - row + n - 1] = true;
                    //递归进下一行
                    dfs(row + 1, n, grid, col, dg, udg,lists,list);
                    //回溯
                    grid[row][i] = '.';
                    col[i] = dg[i + row] = udg[i - row + n - 1] = false;
                }
            }
        }
    }

作者：Alkaidling
链接：https://leetcode-cn.com/problems/n-queens/solution/nhuang-hou-bu-yong-ha-xi-biao-shi-yong-b-d2vj/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。