C语言实现三角分解(Doolittle)法解线性方程组
Doolittle法解线性方程组
- 问题描述
- 算法思想
- 测试数据
- C语言代码
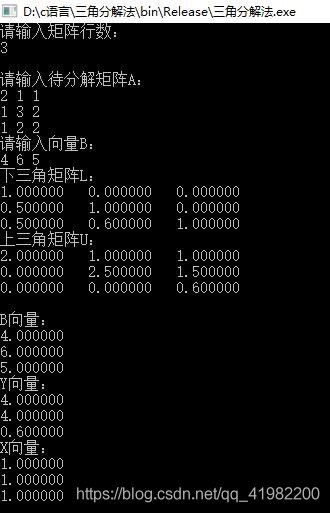
- 实验结果
问题描述
假设 n n n阶线性代数方程组系数矩阵满足所有顺序主子式非奇异,则有 A = L R A=LR A=LR,其中 L , R L,R L,R分别是下三角和上三角阵,而且 L L L或 R R R的对角元素给定后,其分解是唯一的。按照这样的逻辑求解方程组比较容易。
取 L L L为单位下三角阵, A = L R A=LR A=LR,可以表示为:
[ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋯ ⋮ a n 1 a n 1 ⋯ a n n ] = [ 1 0 0 0 l 21 1 0 0 ⋮ ⋮ 1 0 l n 1 l n 2 ⋯ 1 ] = [ r 11 r 12 ⋯ r 1 n 0 r 22 ⋯ r 2 n 0 0 ⋱ ⋮ 0 0 0 r n n ] \quad \begin{bmatrix} a_{11}& {{a_{12}}} & \cdots&{{a_{1n}}} \\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}\\ \vdots & \vdots & \cdots & \vdots \\\\ {{a_{n1}}}&{{a_{n1}}}& \cdots &{{a_{nn}}} \end{bmatrix}=\quad \begin{bmatrix}1&0&0&0\\ {{l_{21}}}&1&0&0\\ \vdots & \vdots &1&0\\ {l_{n1}^{}}&{{l_{n2}}}& \cdots &1 \end{bmatrix} =\quad \begin{bmatrix} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}}\\ 0&{{r_{22}}}& \cdots &{r_{2n}^{}}\\ 0&0& \ddots & \vdots \\ 0&0&0&{{r_{nn}}} \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎡a11a21⋮an1a12a22⋮an1⋯⋯⋯⋯a1na2n⋮ann⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎡1l21⋮ln101⋮ln2001⋯0001⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡r11000r12r2200⋯⋯⋱0r1nr2n⋮rnn⎦⎥⎥⎥⎤
算法思想
比较等号两边第 i i i行第 j j j列的元素,可知
a i j = ∑ k = 1 n l i k r k j {a_{ij}} = \sum\limits_{k = 1}^n {{l_{ik}}{r_{kj}}} aij=k=1∑nlikrkj
注意到, l i , i + 1 = ⋯ = l i n = r j + 1 , j = ⋯ = r n j = 0 {l_{i,i + 1}} = \cdots = {l_{in}} = {r_{j + 1,j}} = \cdots = {r_{nj}} = 0 li,i+1=⋯=lin=rj+1,j=⋯=rnj=0,则上式表示为:
a i j = ∑ k = 1 i l i k r k j = ∑ k = 1 i − 1 l i k r k j + r {{a_{ij}} = \sum\limits_{k = 1}^i {{l_{ik}}{r_{kj}} = \sum\limits_{k = 1}^{i - 1} {{l_{ik}}{r_{kj}}} } + r} aij=k=1∑ilikrkj=k=1∑i−1likrkj+r
从而,
r i j = a i j − ∑ k = 1 i − 1 l i k r k j , j = 1 , 2 , ⋯ , n {{r_{ij}}= {a_{ij}}- \sum\limits_{k = 1}^{i - 1} {{l_{ik}}{r_{kj}}} ,j=1,2, \cdots,n} rij=aij−k=1∑i−1likrkj,j=1,2,⋯,n
当 j = i + 1 , i + 2 ⋯ n j = i + 1,i + 2 \cdots n j=i+1,i+2⋯n时,
a j i = ∑ k = 1 i l j k r k i = ∑ k = 1 i − 1 l j k r k i + l j i r i i {a_{ji}} = \sum\limits_{k = 1}^i {{l_{jk}}{r_{ki}} = } \sum\limits_{k = 1}^{i - 1} {{l_{jk}}{r_{ki}} + {l_{ji}}{r_{ii}}} aji=k=1∑iljkrki=k=1∑i−1ljkrki+ljirii
从而,
l j i = ( a j i − ∑ k = 1 i − 1 l j k r k i ) r i i , j = i + 1 , ⋯ , n {{l_{ji}} = \frac{{({a_{ji}} - \sum\limits_{k = 1}^{i - 1} {{l_{jk}}r_{ki}^{}} )}}{{{r_{ii}}}}},{j = i + 1, \cdots ,n} lji=rii(aji−k=1∑i−1ljkrki),j=i+1,⋯,n
根据以上描述,我们可以将问题表示为: A x = L R x = b Ax=LRx=b Ax=LRx=b
可以分两步进行求解
{ L y = b R x = y \begin{cases} {Ly = b}\\ {Rx = y} \end{cases} {Ly=bRx=y
先求出 y y y,在求出 x x x,其计算公式为
{ y i = b i − ∑ k = 1 i − 1 l i k y k , i = 1 , 2 ⋯ , n x i = ( y i − ∑ k = i + 1 n r i k x k ) r i i , i = n , n − 1 , ⋯ 1 \begin{cases} {{y_i} = {b_i} - \sum\limits_{k = 1}^{i - 1} {{l_{ik}}{y_k}} },{i = 1,2 \cdots ,n}\\ {{x_i} = \frac{{(y_i^{} - \sum\limits_{k = i + 1}^n {{r_{ik}}{x_k}} )}}{{{r_{ii}}}}},{i = n,n - 1, \cdots 1} \end{cases} ⎩⎪⎪⎨⎪⎪⎧yi=bi−k=1∑i−1likyk,i=1,2⋯,nxi=rii(yi−k=i+1∑nrikxk),i=n,n−1,⋯1
测试数据
{ 2 x 1 + x 2 + x 3 = 4 x 1 + 3 x 2 + 2 x 3 = 6 x 1 + 2 x 2 + 2 x 3 = 5 \begin{cases} {2{x_1} + {x_2} + {x_3} = 4}\\ {{x_1} + 3{x_2} + 2{x_3} = 6}\\ {{x_1} + 2{x_2} + 2{x_3} = 5} \end{cases} ⎩⎪⎨⎪⎧2x1+x2+x3=4x1+3x2+2x3=6x1+2x2+2x3=5
先将系数矩阵 A A A按照如上步骤进行 L R LR LR分解
[ 1 0 0 1 / 2 1 0 1 / 2 3 / 5 1 ] [ − 2 1 1 0 5 / 2 3 / 2 0 0 3 / 5 ] \quad \begin{bmatrix} 1&0&0\\{1/2}&1&0\\{1/2}&{3/5}&1 \end{bmatrix} \quad \begin{bmatrix} { - 2}&1&1\\ 0&{5/2}&{3/2}\\ 0&0&{3/5} \end{bmatrix} ⎣⎡11/21/2013/5001⎦⎤⎣⎡−20015/2013/23/5⎦⎤
C语言代码
#include