智能优化算法:斑马优化算法-附代码
智能优化算法:斑马优化算法
文章目录
- 智能优化算法:斑马优化算法
-
- 1.斑马优化算法
-
- 1.1 初始化
- 1.2 阶段一:觅食行为
- 1.3 阶段二:针对捕食者的防御策略
- 2.实验结果
- 3.参考文献
- 4.Matlab
- 5.python
摘要:斑马优化算法(Zebra Optimization Algorithm(ZOA)),是于2022年提出的一种基于斑马行为的优化算法,该算法通过模拟斑马行为来进行寻优,具有寻优能力强,收敛速度快等特点
1.斑马优化算法
1.1 初始化
与其他优化算法类似,在寻优空间里随机初始化种群:
x i , j = l b j + r ⋅ ( u b j − l b j ) , (2) x_{i, j}=l b_j+r \cdot\left(u b_j-l b_j\right) \text {, }\tag{2} xi,j=lbj+r⋅(ubj−lbj), (2)
其中 x i , j x_{i,j} xi,j为个体, l b j lb_j lbj为寻优下边界, u b j ub_j ubj为寻优上边界, r r r为[0,1]之间的随机数。
1.2 阶段一:觅食行为
在第一阶段,种群成员在搜索饲料时根据斑马行为的模拟进行更新。斑马的主要食物主要是草和莎草,但如果它们喜欢的食物稀缺,它们也可能吃花蕾、水果、树皮、根和叶子。根据植被的质量和可用性,斑马可能会花费60-80%的时间进食。在斑马中,有一种被称为平原斑马的斑马,它是一种先锋食草动物,通过吞噬上层和营养较少的草的树冠,为其他需要较矮和营养较多的草的物种提供了条件。在ZOA中,种群中最好的成员被认为是先锋斑马,并将其他种群成员引向其在搜索空间中的位置。因此,可以使用(3)和(4)对斑马在觅食阶段的位置更新进行数学建模。
x i , j n e w , P 1 = x i , j + r ⋅ ( P Z j − I ⋅ x i , j ) (3) x_{i, j}^{n e w, P 1}=x_{i, j}+r \cdot\left(P Z_j-I \cdot x_{i, j}\right) \tag{3} xi,jnew,P1=xi,j+r⋅(PZj−I⋅xi,j)(3)
X i = { X i new , P 1 , F i new , P 1 < F i X i , else (4) X_i= \begin{cases}X_i^{\text {new }, P 1}, & F_i^{\text {new }, P 1}
其中r为[0,1]之间的随机数,I为属于集合{1,2}的随机值。
1.3 阶段二:针对捕食者的防御策略
在第二阶段,模拟斑马对捕食者攻击的防御策略,以更新ZOA种群成员在搜索空间中的位置。斑马的主要捕食者是狮子;然而,它们受到猎豹、豹子、野狗、棕色鬣狗和斑点鬣狗的威胁。鳄鱼是斑马接近水面时的另一种捕食者。斑马的防御策略因捕食者而异。斑马对狮子攻击的防御策略是以Z字形和随机的侧向转弯动作逃跑。斑马对较小的捕食者的攻击更具攻击性,如鬣狗和狗,它们通过聚集来迷惑和恐吓猎人。在ZOA设计中,假设以下两种情况之一以相同的概率发生:
(i) 狮子攻击斑马,因此斑马选择了逃跑策略;
(ii)其他捕食者攻击斑马,斑马会选择攻击策略。
在第一种策略中,当斑马受到狮子的攻击时,斑马会在其所在位置附近躲避狮子的攻击。因此,在数学上,可以使用(5)中的模式S1来对该策略进行建模。在第二种策略中,当其他捕食者攻击其中一只斑马时,群中的其他斑马会向被攻击的斑马靠近,并试图通过建立防御结构来恐吓和迷惑捕食者。使用(5)中的模式S2对斑马的这种策略进行数学建模。在更新斑马的位置时,如果斑马在新位置中的目标函数具有更好的值,则接受该新位置。使用(6)对该更新条件进行建模。
x i , j new , P 2 = { S 1 : x i , j + R ⋅ ( 2 r − 1 ) ⋅ ( 1 − t T ) ⋅ x i , j , P s ≤ 0.5 S 2 : x i , j + r ⋅ ( A Z j − I ⋅ x i , j ) , else , (5) x_{i, j}^{\text {new }, P 2}=\left\{\begin{array}{cl} S_1: x_{i, j}+R \cdot(2 r-1) & \\ \cdot\left(1-\frac{t}{T}\right) \cdot x_{i, j}, & P_s \leq 0.5 \\ S_2: x_{i, j}+r \cdot\left(A Z_j-I \cdot x_{i, j}\right), & \text { else }, \end{array}\right.\tag{5} xi,jnew ,P2=⎩ ⎨ ⎧S1:xi,j+R⋅(2r−1)⋅(1−Tt)⋅xi,j,S2:xi,j+r⋅(AZj−I⋅xi,j),Ps≤0.5 else ,(5)
X i = { X i new , P 2 , F i new , P 2 < F i X i , else , (6) X_i= \begin{cases}X_i^{\text {new }, P 2}, & F_i^{\text {new }, P 2}
其 t t t 是迭代次数, T T T为最大迭代次数, R R R为0.01的常数。 P s P_s Ps为两种策略的切换概率。其值为[0,1]之间的随机数。AZ为被攻击斑马的状态。
算法流程图如下:
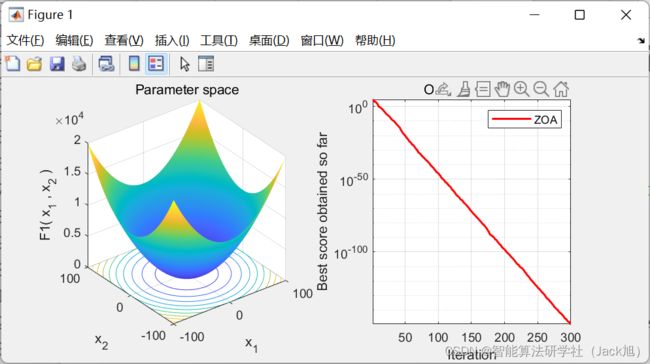
2.实验结果
3.参考文献
[1] E. Trojovská, M. Dehghani and P. Trojovský, “Zebra Optimization Algorithm: A New Bio-Inspired Optimization Algorithm for Solving Optimization Algorithm,” in IEEE Access, vol. 10, pp. 49445-49473, 2022, doi: 10.1109/ACCESS.2022.3172789.