机器人控制算法——TEB算法—Obstacle Avoidance and Robot Footprint Model（避障与机器人足迹模型）

1.How Obstacle Avoidance works

1.1处罚条款

避障是作为整体轨迹优化的一部分来实现的。显然，优化涉及到找到指定成本函数（目标函数）的最小成本解（轨迹）。简单地说：如果一个计划的（未来）姿势违反了与障碍物的期望分离，那么成本函数的成本必须增加。理想情况下，在这些情况下，成本函数值必须是无穷大的，否则优化器可能会更好地完全拒绝这些区域。然而，这将需要优化器处理硬约束（即求解非线性程序）。teb_local_planner放弃了考虑硬约束的能力，以便更好地考虑效率。将硬约束转化为软约束，从而得到具有有限代价的二次罚项。

上图显示了一个示例处罚条款（针对避障）。到障碍物的允许最小欧几里得距离（参数$mi{n}_{o}bstacl{e}_{d}ist$）设置为0.2米。因此，0.2米以下的距离会导致非零成本。现在假设优化问题包含更多的成本项。其中一些是相互冲突的，例如时间最优性。因此，优化器可能会考虑到一个小的违规（因此也会考虑到小的惩罚），以最小化整个组合成本函数。这里有两个选项可以调整行为：
1. 调整优化权重（按比例缩放单个成本，此处为参数weight_obstacle）。但是，如果选择过高的值，优化问题就会变得病态，从而导致较差的便利性行为。
2. 通过添加“额外边距”来改变参数。通过在min_obstacle_dist参数中添加一个小的额外裕度，您可以将成本值隐式地增加到0.2m。您可以使用单个参数penalty_ epsilon同时移动所有惩罚项，但要小心，因为这样做会极大地影响优化结果。

1.2 局部最优解

请注意，优化器本身只能找到局部最优的解决方案。想象一下，机器人可能被两个障碍物横向包裹。惩罚项确实是非零的，但优化器会被卡住（达到这个局部最小值），因为将相应的姿势横向移动到其中一个障碍物会进一步增加总成本。您可以使用test_optim_node轻松尝试（请参阅教程设置和测试优化，并关闭同源类规划）。行为应类似于下图中的行为：

轨迹无法跳过障碍物。即使是姿势本身也被推离障碍物之间的区域（红色箭头）。显然，在实践中应该避免这种情况。因此，同源类规划算法寻求（拓扑）替代解决方案，而可行性检查（见下文）在实际指挥机器人之前拒绝了这样的解决方案。

1.3位势和障碍之间的关联

下图显示了一个常见规划场景的快照：
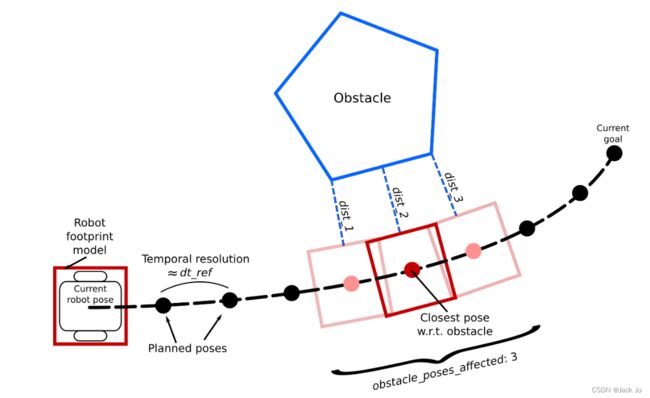该场景由一个移动机器人组成，该机器人在前往当前目标时接近多边形障碍物。计划（离散）轨迹由多个机器人姿态组成。规划者的目标是根据所需的时间分辨率（参数dt_ref）来安排每两个连续的姿势。请注意，实际分辨率不是固定/冻结的，因为优化器需要调整转换时间以寻求时间最优性。
对于避障，计划姿势和障碍物之间的距离必须从下方界定。图中的示例轨迹由8个可变姿势组成（起始姿势和目标姿势是固定的）。您可能同意，为了实现无碰撞轨迹，需要进行多次距离计算（优化器多次调用成本函数值的计算）。为了加速优化，实现了专用的关联策略。
对于每个障碍物（点/占用的成本图单元、线、多边形），定位计划轨迹的最接近姿态（见图）。根据参数obstacle_poses_affected的值，还考虑了最近姿态的受影响邻居。在随后的优化步骤中只考虑该选定的姿态子集（这里是3个姿态，因此是3个惩罚项）。分别在no_inner_iterations（参数）之后重复关联过程。在每个外部优化迭代obstacle_poses_affected的值会略微影响障碍物周围轨迹的平滑度。此外，更大的障碍需要更多的连接姿势，以避免不可错过的捷径。您也可以选择一个较高的值（>轨迹长度），以便将所有姿势与每个障碍物连接起来。
注意，机器人足迹模型被考虑用于距离计算，因此对于所需的计算资源至关重要。以下部分对详细信息进行了总结。

2.Robot Footprint Model 机器人足迹模型

出于优化目的，机器人足迹模型近似机器人的2D轮廓。该模型对于距离计算的复杂性以及计算时间至关重要。因此，机器人足迹模型构成了一个专用参数，而不是从通用的costmap_2d参数加载足迹。优化占地面积模型可能与成本图占地面积模型不同（后者用于可行性检查，请参阅下一节）。
封装外形模型是使用参数服务器选择和配置的。您可以将以下参数结构添加到teb_local_planner配置文件中：

TebLocalPlannerROS:
 footprint_model: # types: "point", "circular", "line", "two_circles", "polygon"
   type: "point"
   radius: 0.2 # for type "circular"
   line_start: [-0.3, 0.0] # for type "line"
   line_end: [0.3, 0.0] # for type "line"
   front_offset: 0.2 # for type "two_circles"
   front_radius: 0.2 # for type "two_circles"
   rear_offset: 0.2 # for type "two_circles"
   rear_radius: 0.2 # for type "two_circles"
   vertices: [ [0.25, -0.05], [0.18, -0.05], [0.18, -0.18], [-0.19, -0.18], [-0.25, 0], [-0.19, 0.18], [0.18, 0.18], [0.18, 0.05], [0.25, 0.05] ] # for type "polygon"

默认示意图模型的类型为“点”。注意，封装外形发布到~/teb_markers，并且可以在rviz中可视化（例如用于验证）。
重要提示：对于类似汽车的机器人，姿态[0,0]位于后轴（旋转轴）！
以下段落描述了所有不同的类型：

2.1迹线类型：点

机器人被建模为单个点。对于这种类型，需要最少的计算时间。

2.2迹线类型：圆形

机器人被建模为一个具有给定半径~/footprint_model/radius的简单圆。距离计算类似于点型机器人的计算，但有了例外，机器人的半径被添加到每个函数调用的参数min_obstacle_dist中。你可以通过选择一个点型机器人并事先将半径添加到最小障碍物距离来消除这种额外的添加。

2.3示意图类型：线条

直线机器人适用于在纵向和横向方向上表现出不同扩展/长度的机器人。可以使用参数_{/footprint_model/line_start和}/footprint _model/line _end（每个[x，y]坐标）来配置线（段）。机器人（旋转轴）假定为[0,0]（单位：米）。请确保通过进一步调整参数min_obstacle_dist来封装整个机器人（参见以下示例）。
你也可以看看“两个圆”模型。

2.4示意图类型：两个圆圈

另一种近似机器人轮廓的可能性包括定义两个圆。每个圆由沿机器人x轴的偏移和半径来描述：_{/footprint_model/front_offset、}/footprint _model/front_radius、~/foot print_model/rear_offset和~/footprint_model/rear_radius。偏移可能为负。
请参考下图作为示例：
对于每个相关的机器人姿势，需要进行两次距离计算。

2.5迹线类型：多边形

可以通过定义闭合多边形来合并复杂模型。多边形是根据顶点列表定义的（为每个顶点提供x和y坐标）。假设机器人的旋转轴位于[0,0]（单位：米）。请不要重复第一个顶点，因为多边形是自动关闭的。请记住，每增加一条边都会显著增加所需的计算时间！您可以从成本图通用参数文件中复制足迹模型。

3可行性检查

在优化器返回轨迹之后，在将速度命令发送到机器人之前，进行可行性检查。此检查的目的是识别优化器可能产生的无效/不可行轨迹（请记住：软约束、局部极小值等）。
目前，该算法从当前机器人姿势开始迭代前n个姿势（n=~/pability_check_no_poses（parameter！）），并检查这些姿势是否没有碰撞。为了检测是否发生碰撞，将使用成本图足迹（请参见导航教程）！因此，这个验证模型可能比用于优化的封装外形更复杂（请参阅上面的一节）。
由于优化器可能无法完全收敛，因此不应选择过高的值~/probability_check_no_poses：形象地说，当机器人向目标移动时，可以纠正（遥远）未来的小障碍违规行为。
如果您在狭窄的环境中驾驶，请确保正确配置避障行为（本地规划器和全局规划器）。否则，局部规划器可能会拒绝不可行的轨迹（从它的角度来看），但相比之下，全局规划器可能进一步认为所选的（全局）计划是可行的：机器人可能会被卡住。

Reference
1.Obstacle Avoidance and Robot Footprint Model