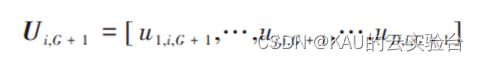超详细 | 差分进化算法原理及其实现(Matlab/Python)
差分进化(Differential Evolution，DE)算法是由美国学者Storn和 Price在1995年为求解Chebyshev多项式拟合问题而提出的。算法主要通过基于差分形式的变异操作和基于概率选择的交叉操作进行优化搜索，虽然其操作名称和遗传算法相同，但实现方法有本质区别。
差分进化算法的原理简单,参数设置较少,易于编程实现,目前已被证明为是一种高效的智能优化算法，已在人工神经网络、电力、机器人、信号处理等领域得到了应用。
本文将介绍其理论模型和代码实现。
00 目录
1 差分进化算法原理
2 代码目录
3 算法性能
4 源码获取
01 差分进化算法原理
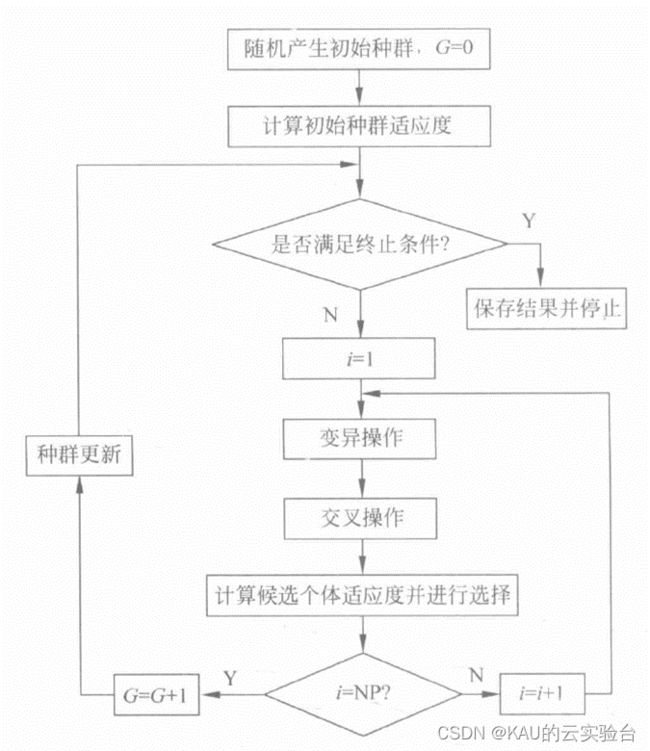
差分进化算法的基本思想源于遗传算法。
变异：DE算法是通过把种群中两个个体之间的加权差向量加到第三个个体上来产生新参数向量;
交叉：将变异向量的参数与另外预先决定的目标向量的参数按照一定的规则混合起来产生子个体;
选择：新产生的子个体只有当它比种群中的目标个体优良时才对其进行替换;
DE算法的选择操作是在完成变异、交叉之后由父代个体与新产生的候选个体――对应地进行竞争，优胜劣汰,使得子代个体总是等于或优于父代个体。
而且,DE算法给予父代所有个体以平等的机会进入下一代,不歧视劣质个体。
差分进化算法把一定比例的多个个体的差分信息作为个体的扰动量,使得算法在跳跃距离和搜索方向上具有自适应性。在进化的早期,因为种群中个体的差异性较大,使得扰动量较大,从而使得算法能够在较大范围内搜索,具有较强的勘探能力﹔到了进化的后期﹐当算法趋向于收敛时,种群中个体的差异性较小,算法在个体附近搜索,这使得算法具有较强的局部开采能力。
正是由于差分进化算法具有向种群个体学习的能力,使得其拥有其他进化算法无法比拟的性能。其具体操作如下：
（1）变异
当种群进化至第 G 代时，对父代个体Xi，G 实施变异操作得到变异个体，即：
式中下标 r1，r2，r3 是在 1 和 NP（种群规模） 之间随机选择的与i不同的互异整数，Xr1,G称为基向量，( Xr2,G - Xr3,G ) 称为差分向量，F为缩放因子。如果变异个体中的参数超出边界，则该参数的值将被边界值替换。
（2）交叉
通过交叉操作产生试验个体为：
其中，
式中 rj[ 0，1) 代表第 j 次计算的随机数，CR 为交叉率。r(i)是在1和D之间随机选取的 整数，可使Ui,G + 1从Vi,G + 1获得至少一个变量。
（3）选择
对于最小化问题，在试验个体Ui,G + 1与父代个体Xi,G中选择目标函数较小的个体进入下一代种群，即：
式中 F (X)代表目标函数。
算法中主要的控制参数为种群规模NP、缩放因子F、交叉率CR，通常这些参数在进化时都保持不变。
算法流程图如下：
02 代码目录
MATLAB
Python
包含MATLAB 和Python的程序，考虑到很多同学获取代码后有乱码（matlab版本问题），可以将matlab版本改为2020-2022，或使用乱码解决文件夹中的txt文件即可。
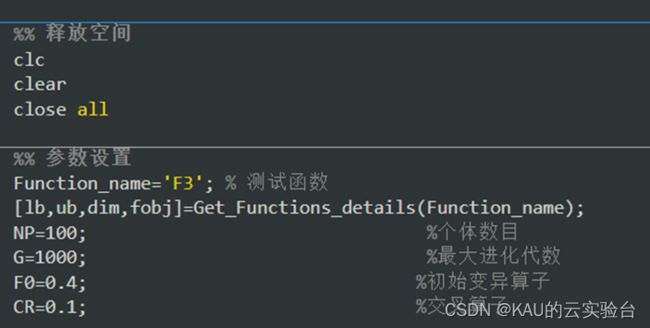
部分代码：
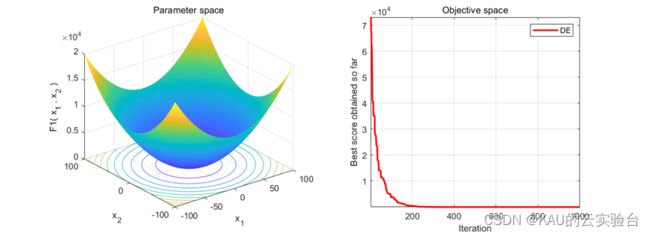
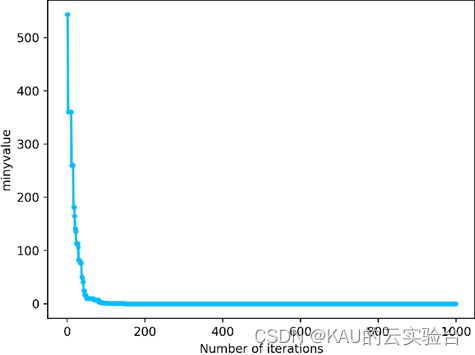
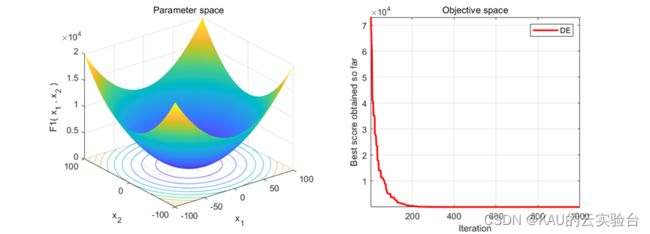
03 算法性能
采用CEC中的测试函数来初步检验其寻优性能，在MATLAB中执行程序结果如下：
在Python中结果：
04 源码获取
在GZH（KAU的云实验台）加粗样式回复 DE 即可
DE算法具有较强的通用性，不依赖于问题信息，且原理简单，容易实现，能够利用个体的局部信息和群体的全局信息指导算法搜索，能够易于与其他算法结合，同样，DE算法也存在局部搜索能力弱、搜索效率低等缺点，为此，可采用不同的变异策略或是种群更新机制等方法提升其性能。
另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行)，你们的鼓励就是我坚持的动力！若有定制需求，可私信作者。