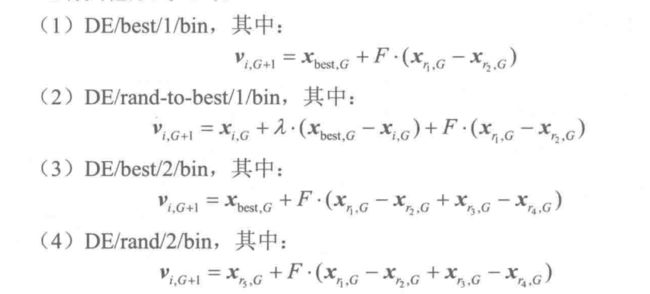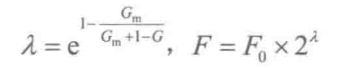两万字长文了解差分进化算法及求解复杂约束问题(源码实现)
前言
文字加代码字母,共21504个字,所以叫两万字长文带你了解差分进化算法。写作不容易,请打赏。
算法原理
差分进化算法是基于群体智能理论的优化算法,是通过群体内个体间的合作与竞争而产生的智能优化搜索算法。但相比于进化计算,它保留了基于种群的全局搜索策略,采用实数编码、基于差分的简单变异操作和“一对一”的竞争生存策略,降低了进化计算操作的复杂性。同时,差分进化算法特有的记忆能力使其可以动态跟踪当前的搜索情况,以调整其搜索策略,它具有较强的全局收敛能力和稳健性,且不需要借助问题的特征信息,适用于求解–些利用常规的数学规划方法很难求解甚至无法求解的复杂优化问题。因此,差分进化算法作为一种高效的并行搜索算法,对其进行理论和应用研究具有重要的学术意义和工程价值。
差分进化算法是一种自组织最小化方法,用户只需很少的输入。它的关键思想与传统进化方法不同:传统方法是用预先确定的概率分布函数决定向量扰动;而差分进化算法的自组织程序利用种群中两个随机选择的不同向量来干扰一个现有向量,种群中的每一个向量都要进行干扰。差分进化算法利用一个向量种群,其中种群向量的随机扰动可独立进行,因此是并行的。如果新向量对应函数值的代价比它们的前辈代价小,它们将取代前辈向量。同其他进化算法一样,差分进化算法也是对候选解的种群进行操作,但其种群繁殖方案与其他进化算法不同:它通过把种群中两个成员之间的加权差向量加到第三个成员上来产生新的参数向量,该操作称为“变异”;然后将变异向量的参数与另外预先确定的目标向量参数按一定规则混合来产生试验向量,该操作称为“交叉”;最后,若试验向量的代价函数比目标向量的代价函数低,试验向量就在下一代中代替目标向量,该操作称为“选择”。种群中所有成员必须当作目标向量进行一次这样的操作,以便在下一代中出现相同个数竞争者。在进化过程中对每一代的最佳参数向量都进行评价,以记录最小化过程。这样利用随机偏差扰动产生新个体的方式,可以获得一个收敛性非常好的结果,引导搜索过程向全局最优解逼近。
基本差分进化算法
流程
- 初始化
- 变异
- 交叉
- 选择
- 边界条件处理
初始化
差分进化算法利用NP个维数为D的实数值参数向量,将它们作为每–代的种群,每个个体表示为:
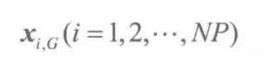
式中: i表示个体在种群中的序列; G表示进化代数: NP表示种群规模,在最小化过程中NP保持不变。 一般初始化,设置数值为上下界限之间的随机数。
![]()
变异
对于每个目标向量xiG(i=1, 2,.,NP), 基本差分进化算法的变异向量由下式产生:
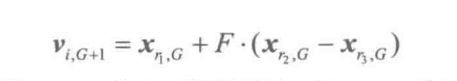
式中:随机选择的序号r、r2和13互不相同,且r、r2和r3与目标向量序号i也应不同,所以必须满足NP≥4;变异算子F∈[0,2]是一个实常数因数,它控制偏差变量的放大作用。
交叉
为了增加干扰参数向量的多样性,引入交叉操作,则试验向量变为:
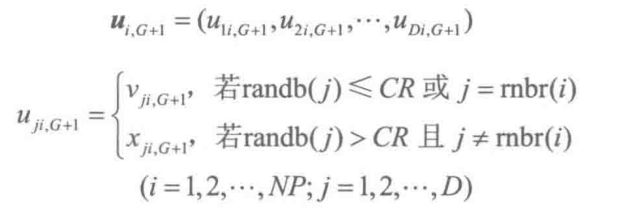
式中: randb(j)表示产生[0, 1]之 间随机数发生器的第j个估计值; rnbr(i)∈(1,2,.,. D)表示一个随机选择的序列,用它来确保Ui,G+1至少从Vi,G+1获得一个参数: CR 表示交叉算子,其取值范围为[0,1]。
选择
为决定试验向量ui,G+1是否会成为下一代中的成员,差分进化算法按照贪婪准则将试验向量与当前种群中的目标向量xi,G进行比较。如果目标函数要被最小化,那么具有较小目标函数值的向量将在下一代种群中出现。下一代中的所有个体都比当前种群的对应个体更佳或者至少一样好。注意:在差分进化算法选择程序中,试验向量只与一个个体相比较,而不是与现有种群中的所有个体相比较。
边界条件处理
判断是否满足约束条件,如果不满足,有两个策略:超出边界的放到边界上。或者超出边界的,重新初始化。
改进的差分算法
式中: Fo 表示变异算子,Gm表示最大进化代数,G表示当前进化代数。在算法开始时自适应变异算子为2Fo,具有较大值,在初期保持个体多样性,避免“早熟”;随着算法的进展,变异算子逐步降低,到后期变异率接近Fo,保留优良信息,避免最优解遭到破坏,增加搜索到全局最优解的概率。
还可设计一个随机范围的交叉算子CR: 0.5*[1 + rand(0,1)],这样交叉算子的平均值保持在0.75,考虑到了差分向量放大中可能的随机变化,有助于在搜索过程中保持群体多样性。
离散差分算法
差分进化算法采用浮点数编码,在连续空间进行优化计算,是一种求解实数
变量优化问题的有效方法。要将差分进化算法用于求解整数规划或混合整数规划问题,必须对差分进化算法进行改进。差分进化算法的基本操作包括变异、交叉和选择操作,与其他进化算法- -样也是依据适应度值大小进行操作。根据差分进化算法的特点,只要对变异操作进行改进就可以将差分进化算法用于整数规划和混合整数规划。对于整数变量,可对差分进化算法变异操作中的差分矢量进行向下取整运算,从而保证整数变量直接在整数空间进行寻优,即:
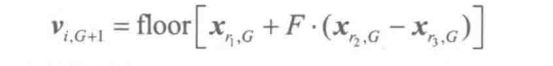
差分算法流程

算例
MATLAB求解
%%%%%%%%%%%%%%%%%差分进化算法求函数极值%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
NP=50; %个体数目
D=10; %变量的维数
G=200; %最大进化代数
F0=0.4; %初始变异算子
CR=0.1; %交叉算子
Xs=20; %上限
Xx=-20; %下限
yz=10^-6; %阈值
%%%%%%%%%%%%%%%%%%%%%%%%%赋初值%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(D,NP); %初始种群
v=zeros(D,NP); %变异种群
u=zeros(D,NP); %选择种群
x=rand(D,NP)*(Xs-Xx)+Xx; %赋初值
%%%%%%%%%%%%%%%%%%%%计算目标函数%%%%%%%%%%%%%%%%%%%%
for m=1:NP
Ob(m)=func1(x(:,m));
end
trace(1)=min(Ob);
%%%%%%%%%%%%%%%%%%%%%%%差分进化循环%%%%%%%%%%%%%%%%%%%%%
for gen=1:G
%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%自适应变异算子%%%%%%%%%%%%%%%%%%%
lamda=exp(1-G/(G+1-gen));
F=F0*2^(lamda);
%%%%%%%%%%%%%%%%%r1,r2,r3和m互不相同%%%%%%%%%%%%%%%%
for m=1:NP
r1=randi([1,NP],1,1);
while (r1==m)
r1=randi([1,NP],1,1);
end
r2=randi([1,NP],1,1);
while (r2==m)|(r2==r1)
r2=randi([1,NP],1,1);
end
r3=randi([1,NP],1,1);
while (r3==m)|(r3==r1)|(r3==r2)
r3=randi([1,NP],1,1);
end
v(:,m)=x(:,r1)+F*(x(:,r2)-x(:,r3));
end
%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%
r=randi([1,D],1,1);
for n=1:D
cr=rand(1);
if (cr<=CR)|(n==r)
u(n,:)=v(n,:);
else
u(n,:)=x(n,:);
end
end
%%%%%%%%%%%%%%%%%%%边界条件的处理%%%%%%%%%%%%%%%%%%%%%
for n=1:D
for m=1:NP
if (u(n,m)<Xx)|(u(n,m)>Xs)
u(n,m)=rand*(Xs-Xx)+Xx;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%
for m=1:NP
Ob1(m)=func1(u(:,m));
end
for m=1:NP
if Ob1(m)<Ob(m)
x(:,m)=u(:,m);
end
end
for m=1:NP
Ob(m)=func1(x(:,m));
end
trace(gen+1)=min(Ob);
if min(Ob(m))<yz
break
end
end
[SortOb,Index]=sort(Ob);
x=x(:,Index);
X=x(:,1) %最优变量
Y=min(Ob) %最优值
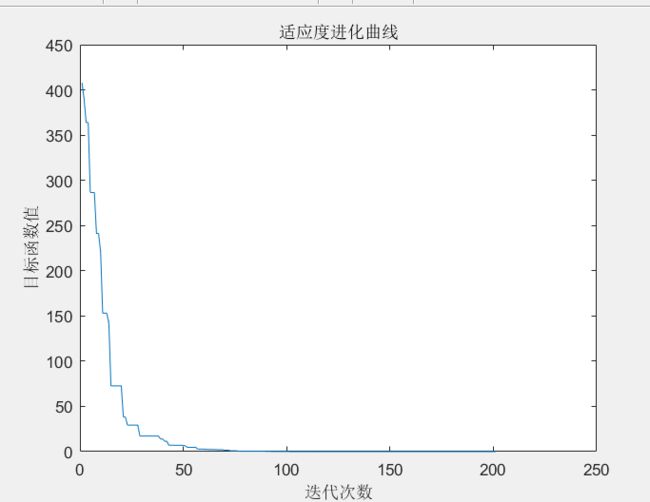
%%%%%%%%%%%%%%%%%%%%%%%%%画图%%%%%%%%%%%%%%%%%%%%%%%%%%
figure
plot(trace);
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%%%%%
function result=func1(x)
summ=sum(x.^2);
result=summ;
end

python求解
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu(余登武)
# @Date : 2021/4/24
#@email:[email protected]
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
##########适应度函数##################
def func1(x):
SUM = [i * i for i in x]
return np.sum(SUM)
##################初始化##############
NP = 50 # 个体数目
D = 10 # 变量的维数
G = 200 # 最大进化代数
F0 = 0.4 # 初始变异算子
CR = 0.1 # 交叉算子
Xs = 20; # 上限
Xx = -20 # 下限
yz = 10e-6 # 阈值
ob = np.zeros(NP) # 存放个体目标函数值(父辈)
ob1 = np.zeros(NP) # 存放个体目标函数值(子代)
##################赋初值##############
x = np.zeros((NP, D)) # 初始种群 (个体数目,维数)
v = np.zeros((NP, D)) # 变异种群 (个体数目,维数)
u = np.zeros((NP, D)); # 选择种群 (个体数目,维数)
x = np.random.uniform(Xx, Xs, (NP, D)) # 赋初值 (xx-xs之间的随机数 ,(个体数目,维数)
trace = [] # 记录每次迭代的最小适应值
###################计算当前群体个体目标函数值#############
for i in range(NP): # 遍历每一个个体
ob[i] = func1(x[i, :])
trace.append(np.min(ob))
###################差分进化循环#############
for gen in range(G): # 遍历每一代
############变异操作###########
# 自适应变异算子
lambda1 = np.exp(1 - G / (G + 1 - gen))
F = F0 * np.power(2, lambda1)
############r1,r2,r3和m互不相同########
for m in range(NP): # 遍历每一个个体
r1=np.random.randint(0,NP,1)
while r1==m: #r1不能取m
r1 = np.random.randint(0, NP, 1)
r2=np.random.randint(0,NP,1)
while (r2==m) or (r2==r1): #r2不能取m 和r1
r2 = np.random.randint(0, NP, 1)
r3 = np.random.randint(0, NP, 1)
while (r3==m) or (r3==r2) or (r3==r1):#r3不能取m,r2,r1
r3 = np.random.randint(0, NP, 1)
v[m,:]=x[r1,:]+F*(x[r2,:]-x[r3,:]) #v.shape =(50, 10) 存放的是变异后的种群
######交叉操作######
r = np.random.randint(0, D, 1) #随机选择维度 (即选择x的一维)
for n in range(D):#遍历每一个维度
cr=np.random.random() #生成一个0-1之间的随机数
if (cr<CR) or (n==r):#如果随机数小于交叉算子 或者 当前维数 等于r
u[:,n]=v[:,n] #则选择群体个体维数 为变异后的维数
else:
u[:, n]=x[:,n] #为原始维度
#####边界条件处理####
for m in range(NP):#遍历每一个个体
for n in range(D): # 遍历每一个维度
if (u[m,n]<Xx) or (u[m,n]>Xs):#如果当前元素不处于最大值和最小值之间
u[m, n]=np.random.uniform(Xx, Xs)#则重新初始化该元素
#####选择操作####
for m in range(NP):#遍历每一个个体
ob1[m]=func1(u[m,:]) #计算子代个体适应度值
for m in range(NP): # 遍历每一个个体
if ob1[m]<ob[m]:#如果子代个体适应度值小于父代个体适应度值
x[m,:]=u[m,:]#则替换个体
for m in range(NP): # 遍历每一个个体
ob[m]=func1(x[m,:]) #修改父代适应度值
trace.append(min(ob))#记录当代最优适应度值
index=np.argmin(ob)#取出最小值所在位置索引
print('最优值解\n',x[index,:])
print('最优值\n',func1(x[index,:]))
plt.plot(trace)
plt.title('迭代曲线')
plt.show()
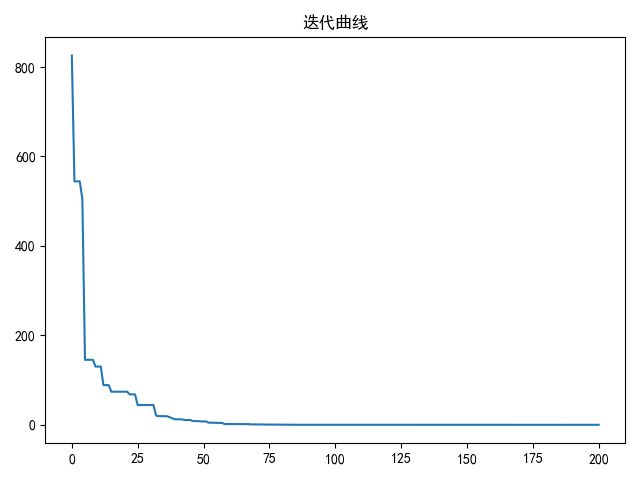

算例2
求函数f(x, y) = 3cos(xy) +x +y的最小值,其中x的取值范围为[-4,4], y的取值范围为[-4, 4]。 这是一个有多个局部极值的函数。
MATLAB版求解
代码中 未使用自适应算子
%%%%%%%%%%%%%%%%%差分进化算法求函数极值%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
NP=20; %个体数目
D=2; %变量的维数
G=100; %最大进化代数
F=0.5; %变异算子
CR=0.1; %交叉算子
Xs=4; %上限
Xx=-4; %下限
%%%%%%%%%%%%%%%%%%%%%%%%%赋初值%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(D,NP); %初始种群
v=zeros(D,NP); %变异种群
u=zeros(D,NP); %选择种群
x=rand(D,NP)*(Xs-Xx)+Xx; %赋初值
%%%%%%%%%%%%%%%%%%%%计算目标函数%%%%%%%%%%%%%%%%%%%%%%%
for m=1:NP
Ob(m)=func2(x(:,m));
end
trace(1)=min(Ob);
%%%%%%%%%%%%%%%%%%%%%%%差分进化循环%%%%%%%%%%%%%%%%%%%%%
for gen=1:G
%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%r1,r2,r3和m互不相同%%%%%%%%%%%%%%%
for m=1:NP
r1=randi([1,NP],1,1);
while (r1==m)
r1=randi([1,NP],1,1);
end
r2=randi([1,NP],1,1);
while (r2==m)|(r2==r1)
r2=randi([1,NP],1,1);
end
r3=randi([1,NP],1,1);
while (r3==m)|(r3==r1)|(r3==r2)
r3=randi([1,NP],1,1);
end
v(:,m)=x(:,r1)+F*(x(:,r2)-x(:,r3));
end
%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%
r=randi([1,D],1,1);
for n=1:D
cr=rand(1);
if (cr<=CR)|(n==r)
u(n,:)=v(n,:);
else
u(n,:)=x(n,:);
end
end
%%%%%%%%%%%%%%%%%%%边界条件的处理%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%边界吸收%%%%%%%%%%%%%%%%%%%%%%%%%
for n=1:D
for m=1:NP
if u(n,m)<Xx
u(n,m)=Xx;
end
if u(n,m)>Xs
u(n,m)=Xs;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%
for m=1:NP
Ob1(m)=func2(u(:,m));
end
for m=1:NP
if Ob1(m)<Ob(m)
x(:,m)=u(:,m);
end
end
for m=1:NP
Ob(m)=func2(x(:,m));
end
trace(gen+1)=min(Ob);
end
[SortOb,Index]=sort(Ob);
x=x(:,Index);
X=x(:,1) %最优变量
Y=min(Ob) %最优值
%%%%%%%%%%%%%%%%%%%%%%%%%画图%%%%%%%%%%%%%%%%%%%%%%%%%%
figure
plot(trace);
xlabel('迭代次数')
ylabel('目标函数值')
title('DE目标函数曲线')
%%%%%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%%%%%%
function value=func2(x)
value=3*cos(x(1)*x(2))+x(1)+x(2);
end
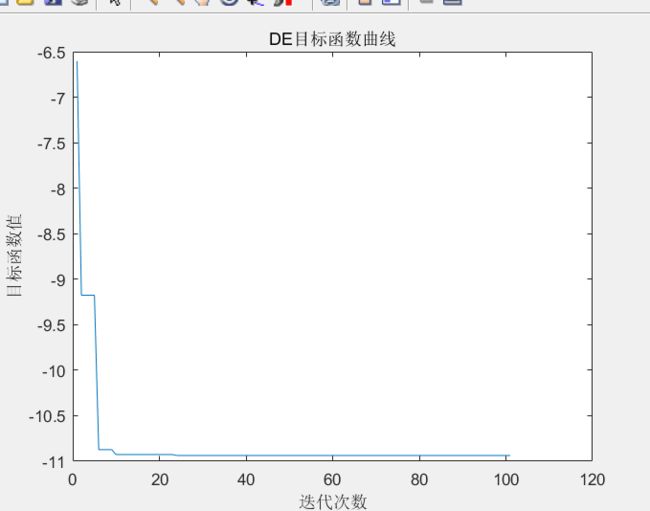

python版求解
代码中 未使用自适应算子
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu(余登武)
# @Date : 2021/4/24
#@email:[email protected]
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
##########适应度函数##################
def func2(x):
value = 3 * np.cos(x[0] * x[1]) + x[0] + x[1]
return value
##################初始化##############
NP=20 #个体数目
D=2 #变量的维数
G=12 #最大进化代数
F=0.5 #变异算子
CR=0.1 #交叉算子
Xs=4 #上限
Xx=-4 #下限
ob = np.zeros(NP) # 存放个体目标函数值(父辈)
ob1 = np.zeros(NP) # 存放个体目标函数值(子代)
##################赋初值##############
x = np.zeros((NP, D)) # 初始种群 (个体数目,维数)
v = np.zeros((NP, D)) # 变异种群 (个体数目,维数)
u = np.zeros((NP, D)); # 选择种群 (个体数目,维数)
x = np.random.uniform(Xx, Xs, (NP, D)) # 赋初值 (xx-xs之间的随机数 ,(个体数目,维数)
trace = [] # 记录每次迭代的最小适应值
###################计算当前群体个体目标函数值#############
for i in range(NP): # 遍历每一个个体
ob[i] = func2(x[i, :])
trace.append(np.min(ob))
###################差分进化循环#############
for gen in range(G): # 遍历每一代
############变异操作###########
############r1,r2,r3和m互不相同########
for m in range(NP): # 遍历每一个个体
r1 = np.random.randint(0, NP, 1)
while r1 == m: # r1不能取m
r1 = np.random.randint(0, NP, 1)
r2 = np.random.randint(0, NP, 1)
while (r2 == m) or (r2 == r1): # r2不能取m 和r1
r2 = np.random.randint(0, NP, 1)
r3 = np.random.randint(0, NP, 1)
while (r3 == m) or (r3 == r2) or (r3 == r1): # r3不能取m,r2,r1
r3 = np.random.randint(0, NP, 1)
v[m, :] = x[r1, :] + F * (x[r2, :] - x[r3, :]) # v.shape =(20, 2) 存放的是变异后的种群
######交叉操作######
r = np.random.randint(0, D, 1) # 随机选择维度 (即选择x的一维)
for n in range(D): # 遍历每一个维度
cr = np.random.random() # 生成一个0-1之间的随机数
if (cr < CR) or (n == r): # 如果随机数小于交叉算子 或者 当前维数 等于r
u[:, n] = v[:, n] # 则选择群体个体维数 为变异后的维数
else:
u[:, n] = x[:, n] # 为原始维度
#####边界条件处理####
for m in range(NP): # 遍历每一个个体
for n in range(D): # 遍历每一个维度
if (u[m, n] < Xx) or (u[m, n] > Xs): # 如果当前元素不处于最大值和最小值之间
u[m, n] = np.random.uniform(Xx, Xs) # 则重新初始化该元素
#####选择操作####
for m in range(NP): # 遍历每一个个体
ob1[m] = func2(u[m, :]) # 计算子代个体适应度值
for m in range(NP): # 遍历每一个个体
if ob1[m] < ob[m]: # 如果子代个体适应度值小于父代个体适应度值
x[m, :] = u[m, :] # 则替换个体
for m in range(NP): # 遍历每一个个体
ob[m] = func2(x[m, :]) # 修改父代适应度值
trace.append(min(ob)) # 记录当代最优适应度值
index=np.argmin(ob)#取出最小值所在位置索引
print('最优值解\n',x[index,:])
print('最优值\n',func2(x[index,:]))
plt.plot(trace)
plt.title('迭代曲线')
plt.show()

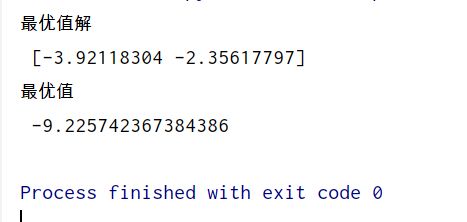
算例3:离散差分算法
用离散差分进化算法求函数f(x,y)= -((x2 +y- 1)+(x+y3- -7)2) /200+10的最大值,其中x的取值为- 100~ 100之间的整数, y的取值为一100~ 100之间的整数。
MATLAB 版求解
%%%%%%%%%%%%%%%%%离散差分进化算法求函数极值%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
NP=20; %个体数目
D=2; %变量的维数
G=100; %最大进化代数
F=0.5; %变异算子
CR=0.1; %交叉算子
Xs=100; %上限
Xx=-100; %下限
%%%%%%%%%%%%%%%%%%%%%%%%%赋初值%%%%%%%%%%%%%%%%%%%%%%%%
x=zeros(D,NP); %初始种群
v=zeros(D,NP); %变异种群
u=zeros(D,NP); %选择种群
x=randi([Xx,Xs],D,NP); %赋初值
%%%%%%%%%%%%%%%%%%%%计算目标函数%%%%%%%%%%%%%%%%%%%%%%%
for m=1:NP
Ob(m)=func3(x(:,m));
end
trace(1)=max(Ob);
%%%%%%%%%%%%%%%%%%%%%%%差分进化循环%%%%%%%%%%%%%%%%%%%%%
for gen=1:G
%%%%%%%%%%%%%%%%%%%%%%变异操作%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%r1,r2,r3和m互不相同%%%%%%%%%%%%%%%
for m=1:NP
r1=randi([1,NP],1,1);
while (r1==m)
r1=randi([1,NP],1,1);
end
r2=randi([1,NP],1,1);
while (r2==m)|(r2==r1)
r2=randi([1,NP],1,1);
end
r3=randi([1,NP],1,1);
while (r3==m)|(r3==r1)|(r3==r2)
r3=randi([1,NP],1,1);
end
v(:,m)=floor(x(:,r1)+F*(x(:,r2)-x(:,r3)));
end
%%%%%%%%%%%%%%%%%%%%%%交叉操作%%%%%%%%%%%%%%%%%%%%%%%
r=randi([1,D],1,1);
for n=1:D
cr=rand(1);
if (cr<=CR)|(n==r)
u(n,:)=v(n,:);
else
u(n,:)=x(n,:);
end
end
%%%%%%%%%%%%%%%%%%%边界条件的处理%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%边界吸收%%%%%%%%%%%%%%%%%%%%%%%%%
for n=1:D
for m=1:NP
if u(n,m)<Xx
u(n,m)=Xx;
end
if u(n,m)>Xs
u(n,m)=Xs;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%选择操作%%%%%%%%%%%%%%%%%%%%%%%
for m=1:NP
Ob1(m)=func3(u(:,m));
end
for m=1:NP
if Ob1(m)>Ob(m)
x(:,m)=u(:,m);
end
end
for m=1:NP
Ob(m)=func3(x(:,m));
end
trace(gen+1)=max(Ob);
end
[SortOb,Index]=sort(Ob);
X=x(:,Index);
Xbest=X(:,end) %最优变量
Y=max(Ob) %最优值
%%%%%%%%%%%%%%%%%%%%%%%%%画图%%%%%%%%%%%%%%%%%%%%%%%%%%
figure
plot(trace);
xlabel('迭代次数')
ylabel('目标函数值')
title('DE目标函数曲线')
%%%%%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%%%%%%%%%%%
function y=func3(x)
y=-((x(1).^2+x(2)-1).^2+(x(1)+x(2).^2-7).^2)/200+10;
end

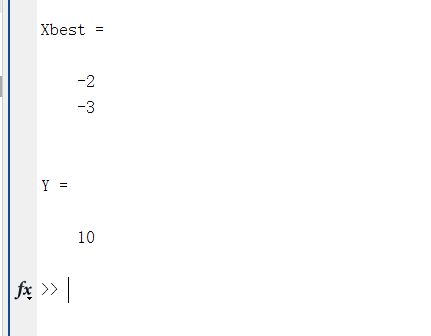
python 版求解
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu(余登武)
# @Date : 2021/4/24
#@email:[email protected]
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
##########适应度函数##################
def func3(x):
value=-(np.power(x[0]*x[0]+x[1]-1,2)+np.power(x[0]+x[1]*x[1]-7,2)/200)+10
return value
#print(func3([-2,-3]))
##################初始化##############
NP=20 #个体数目
D=2 #变量的维数
G=100 #最大进化代数
F=0.5 #变异算子
CR=0.1 #交叉算子
Xs=100 #上限
Xx=-100 #下限
ob = np.zeros(NP) # 存放个体目标函数值(父辈)
ob1 = np.zeros(NP) # 存放个体目标函数值(子代)
##################赋初值##############
x = np.zeros((NP, D)) # 初始种群 (个体数目,维数)
v = np.zeros((NP, D)) # 变异种群 (个体数目,维数)
u = np.zeros((NP, D)); # 选择种群 (个体数目,维数)
x = np.random.randint(Xx, Xs, (NP, D)) # 赋初值 (xx-xs之间的随机整数 ,(个体数目,维数)
trace = [] # 记录每次迭代的最小适应值
###################计算当前群体个体目标函数值#############
for i in range(NP): # 遍历每一个个体
ob[i] = func3(x[i, :])
trace.append(np.max(ob))
###################差分进化循环#############
for gen in range(G): # 遍历每一代
############变异操作###########
############r1,r2,r3和m互不相同########
for m in range(NP): # 遍历每一个个体
r1 = np.random.randint(0, NP, 1)
while r1 == m: # r1不能取m
r1 = np.random.randint(0, NP, 1)
r2 = np.random.randint(0, NP, 1)
while (r2 == m) or (r2 == r1): # r2不能取m 和r1
r2 = np.random.randint(0, NP, 1)
r3 = np.random.randint(0, NP, 1)
while (r3 == m) or (r3 == r2) or (r3 == r1): # r3不能取m,r2,r1
r3 = np.random.randint(0, NP, 1)
v[m, :] = np.floor(x[r1, :] + F * (x[r2, :] - x[r3, :])) # v.shape =(20, 2) 存放的是变异后的种群 np.floor 向下取整
######交叉操作######
r = np.random.randint(0, D, 1) # 随机选择维度 (即选择x的一维)
for n in range(D): # 遍历每一个维度
cr = np.random.random() # 生成一个0-1之间的随机数
if (cr < CR) or (n == r): # 如果随机数小于交叉算子 或者 当前维数 等于r
u[:, n] = v[:, n] # 则选择群体个体维数 为变异后的维数
else:
u[:, n] = x[:, n] # 为原始维度
#####边界条件处理####
for m in range(NP): # 遍历每一个个体
for n in range(D): # 遍历每一个维度
if (u[m, n] < Xx) or (u[m, n] > Xs): # 如果当前元素不处于最大值和最小值之间
u[m, n] = np.random.randint(Xx, Xs) # 则重新初始化该元素
#####选择操作####
for m in range(NP): # 遍历每一个个体
ob1[m] = func3(u[m, :]) # 计算子代个体适应度值
for m in range(NP): # 遍历每一个个体
if ob1[m] > ob[m]: # 如果子代个体适应度值大于父代个体适应度值
x[m, :] = u[m, :] # 则替换个体
for m in range(NP): # 遍历每一个个体
ob[m] = func3(x[m, :]) # 修改父代适应度值
trace.append(max(ob)) # 记录当代最优适应度值
index = np.argmax(ob) # 取出最小值所在位置索引
print('最优值解\n', x[index, :])
print('最优值\n', func3(x[index, :]))
plt.plot(trace)
plt.title('迭代曲线')
plt.show()

求解复杂约束问题
由于差分进算法和遗传算法比较相似,所以求解带约束问题,我套用之前遗传算法的策略。
遗传算法求解带约束优化问题(源码实现)
求解方法
- 一开始设计编码规则时,让解编码就只可能在可行区域内。典型的例子是遗传算法做实数函数的优化,会给出 upper bound和lower bound,然后无论怎样的染色体,解码后都在这两个bound之间 。此方法前面的《万字字符长文带你了解遗传算法(有几个算例源码)》算例中有。
- 设计合理的交叉算子和变异算子,使得满足这些算子本身的特性的前提下,还让算子运算后的染色体也在可行域内。此方法 例子见TSP求解。此方法比较难写。
- 罚函数法。万能方法。但罚函数太多或太严格,会导致效果很差。惩罚系数较大,族群会更加集中在可行域中,而不鼓励向不可行域探索。当惩罚系数过大,容易使算法收敛于局部最优;惩罚系数较小,族群会更积极在不可行域中进行大量探索,一定程度上能帮助寻找全局最优,但也有浪费算力的风险。当惩罚系数过小,算法可能会收敛于不可行解。
- 在变异/交叉之后加入一个判断语句,判断是否满足约束条件,如果不满足,有两个策略:超出边界的放到边界上。或者超出边界的,重新初始化。
算例
python 求解
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu(余登武)
# @Date : 2021/4/24
#@email:[email protected]
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
########################这里定义一些参数,分别是计算适应度函数和计算约束惩罚项函数############
def calc_f(X):
"""计算群体粒子的目标函数值,X 的维度是 size * 2 """
a = 10
pi = np.pi
x = X[0]
y = X[1]
return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)
def calc_e(X):
"""计算群体粒子的目惩罚项,X 的维度是 size * 2 """
ee = 0
"""计算第一个约束的惩罚项"""
e1 = X[0] + X[1] - 6
ee += max(0, e1)
"""计算第二个约束的惩罚项"""
e2 = 3 * X[0] - 2 * X[1] - 5
ee += max(0, e2)
return ee
#子代和父辈之间的选择操作
def update_best(parent,parent_fitness,parent_e,child,child_fitness,child_e):
"""
判
:param parent: 父辈个体
:param parent_fitness:父辈适应度值
:param parent_e :父辈惩罚项
:param child: 子代个体
:param child_fitness 子代适应度值
:param child_e :子代惩罚项
:return: 父辈 和子代中较优者、适应度、惩罚项
"""
# 规则1,如果 parent 和 child 都没有违反约束,则取适应度小的
if parent_e <= 0.0000001 and child_e <= 0.0000001:
if parent_fitness <= child_fitness:
return parent,parent_fitness,parent_e
else:
return child,child_fitness,child_e
# 规则2,如果child违反约束而parent没有违反约束,则取parent
if parent_e < 0.0000001 and child_e >= 0.0000001:
return parent,parent_fitness,parent_e
# 规则3,如果parent违反约束而child没有违反约束,则取child
if parent_e >= 0.0000001 and child_e < 0.0000001:
return child,child_fitness,child_e
# 规则4,如果两个都违反约束,则取适应度值小的
if parent_fitness <= child_fitness:
return parent,parent_fitness,parent_e
else:
return child,child_fitness,child_e
####################初始化参数#####################
NP=50 #种群数量
D=2 # 对应x,y
G=150 #最大遗传代数
F0=0.1 #变异算子
CR=0.1 #交叉算子
Xmax=2 #x上限
Xmin=1 #x下限
Ymax=0 #y上限
Ymin=-1 #y 下限
fit = np.zeros(NP) # 存放个体目标函数值(父辈)
fit1 = np.zeros(NP) # 存放个体目标函数值(子代)
ee=np.zeros(NP) # 存放个体惩罚项(父辈)
ee1=np.zeros(NP) # 存放个体惩罚项(子代)
fitness=np.zeros(NP) # 存放个体适应度值(父辈)
fitness1=np.zeros(NP) # 存放个体适应度值(子代)
##################赋初值##############
x = np.zeros((NP, D)) # 初始种群 (个体数目,维数)
v = np.zeros((NP, D)) # 变异种群 (个体数目,维数)
u = np.zeros((NP, D)); # 选择种群 (个体数目,维数)
x = np.random.uniform(-1, 2, (NP, D)) # 赋初值 (xx-xs之间的随机整数 ,(个体数目,维数)
trace = [] # 记录每次迭代的最小适应值
###################计算当前群体个体目标函数值#############
for i in range(NP): # 遍历每一个个体
fit[i]=calc_f(x[i, :])#目标函数值
ee[i]=calc_e(x[i, :]) #惩罚项
fitness[i] = fit[i]+ee[i] #适应度值
trace.append(np.min(fitness))
###################差分进化循环#############
for gen in range(G): # 遍历每一代
############变异操作###########
############r1,r2,r3和m互不相同########
for m in range(NP): # 遍历每一个个体
lambda1 = np.exp(1 - G / (G + 1 - gen))
F = F0 * np.power(2, lambda1)
############r1,r2,r3和m互不相同########
for m in range(NP): # 遍历每一个个体
r1 = np.random.randint(0, NP, 1)
while r1 == m: # r1不能取m
r1 = np.random.randint(0, NP, 1)
r2 = np.random.randint(0, NP, 1)
while (r2 == m) or (r2 == r1): # r2不能取m 和r1
r2 = np.random.randint(0, NP, 1)
r3 = np.random.randint(0, NP, 1)
while (r3 == m) or (r3 == r2) or (r3 == r1): # r3不能取m,r2,r1
r3 = np.random.randint(0, NP, 1)
v[m, :] = x[r1, :] + F * (x[r2, :] - x[r3, :]) # v.shape =(50, 10) 存放的是变异后的种群
######交叉操作######
r = np.random.randint(0, D, 1) # 随机选择维度 (即选择x的一维)
for n in range(D): # 遍历每一个维度
cr = np.random.random() # 生成一个0-1之间的随机数
if (cr < CR) or (n == r): # 如果随机数小于交叉算子 或者 当前维数 等于r
u[:, n] = v[:, n] # 则选择群体个体维数 为变异后的维数
else:
u[:, n] = x[:, n] # 为原始维度
#####边界条件处理####
for m in range(NP): # 遍历每一个个体
# 判断u[m,:]是否越限 u[m,0]=x,u[m,1]=y
if u[m, 0] > Xmax or u[m, 0] < Xmin:
u[m, 0] = np.random.uniform(Xmin, Xmax)
if u[m, 1] > Ymax or u[m, 1] < Ymin:
u[m, 1] = np.random.uniform(Ymin, Ymax)
#####选择操作####
for m in range(NP): # 遍历每一个个体
fit1[m]=calc_f(x[m, :])#目标函数值 子代
ee1[m] = calc_e(x[m, :]) # 惩罚项 子代
fitness1[m] = fit1[m] + ee1[m] #适应度值 子代
for m in range(NP): # 遍历每一个个体
#update_best(parent, parent_fitness, parent_e, child, child_fitness, child_e)
child,child_fitness,child_e=update_best(x[m],fitness[m],ee[m],u[m],fitness1[m],ee1[m] )
x[m]= child#替换个体
fitness[m]=child_fitness #替换适应度值
ee[m]=child_e #替换惩罚项
trace.append(min(fitness)) # 记录当代最优适应度值
index = np.argmin(fitness) # 取出最小值所在位置索引
print('最优值解\n', x[index, :])
print('最优值\n',fit[index])
plt.plot(trace)
plt.title('迭代曲线')
plt.show()


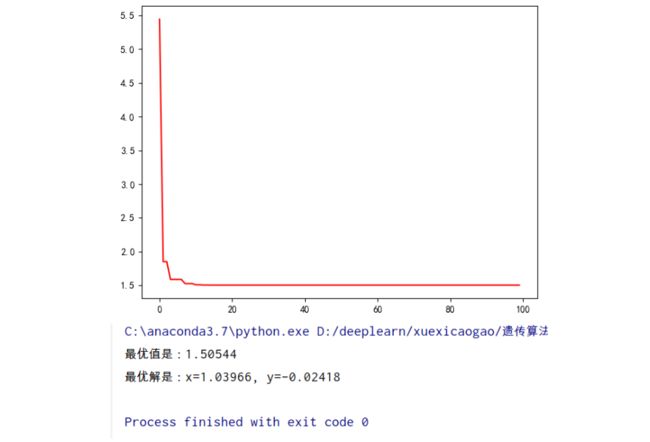
结果相同,都为1.5。因为这个函数图向有很多点都可以取到值为1.5。所以x坐标不一样。这差分进化也太好了吧。一次迭代就求得了最优解? 先不管啦,代码好像没错,(因为结果对的)后面我再探讨下为什么这么优秀。