【LeetCode】73. 矩阵置零

1 问题

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

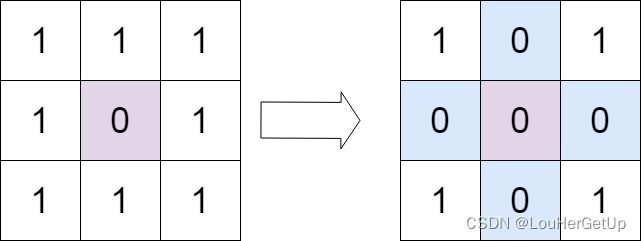
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

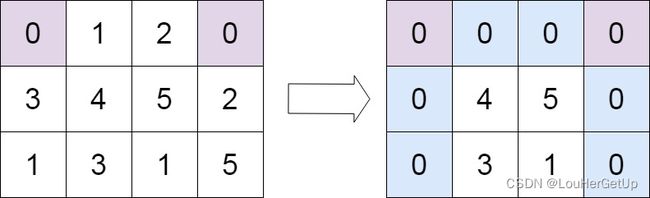
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

2 答案

这题写到一半没思路了，其实再建一个 m x n 的矩阵就可以，用来存储 0 的位置（类似官方解1中的copy一份），这样使用的是 O(m x n) 的额外空间

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:

        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if matrix[i][j] == 0:

官方解

1. 用 O(m x n) 额外空间

把输入的原始数组 copy 一份，那么根据 copy 出来的数组判断某个位置是否为 0，就是原始数组中的该位置是0。遇到 matrix_copy 的一个位置是 0，那么直接修改 matrix 的行列全部是 0。

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        matrix_copy = copy.deepcopy(matrix)  # 深拷贝，独立于原始对象，不共享任何子对象
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if matrix_copy[i][j] == 0:
                    for k in range(len(matrix)):
                        matrix[k][j] = 0
                    for k in range(len(matrix[0])):
                        matrix[i][k] = 0

https://leetcode.cn/problems/set-matrix-zeroes/solutions/670392/xiang-jie-ge-chong-kong-jian-fu-za-du-de-y4pd/

2. 用 O(m+n) 额外空间

两遍扫matrix,第一遍用集合记录哪些行,哪些列有0;第二遍置0

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        row_zero = set()  # 用集合
        col_zero = set()
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if matrix[i][j] == 0:
                    row_zero.add(i)
                    col_zero.add(j)
        for i in range(len(matrix)):
            for j in range(len(matrix[0])):
                if i in row_zero or j in col_zero:
                    matrix[i][j] = 0

3. 用 O(1) 空间

用 matrix 第一行和第一列记录该行该列是否有0,作为标志位

对于第一行和第一列要设置一个标志位，以防止自己这一行(一列)也有0的情况

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        flag_col = False  # 只选择第一列作为标志位
        row = len(matrix)
        col = len(matrix[0])
        for i in range(row):
            if matrix[i][0] == 0: flag_col = True
            for j in range(1,col):  # 第一列作为标志位，不用遍历
                if matrix[i][j] == 0:
                    matrix[i][0] = matrix[0][j] = 0  # 把第一行和第一列作为标志位
        
        for i in range(row - 1, -1, -1):  # 因为第一行第一列为标识符行列，若正序遍历，会首先对第一行进行重置，这样便会将之前本身记录好的标识覆盖，进而再对第二第三行进行重制时，就会出错。
            for j in range(col - 1, 0, -1):   # 第一列作为标志位，不用遍历
                if matrix[i][0] == 0 or matrix[0][j] == 0:  # 两个条件可以用or连接起来
                    matrix[i][j] = 0

            if flag_col == True: matrix[i][0] = 0  # 如果为True，第一列全部赋为0

https://leetcode.cn/problems/set-matrix-zeroes/solutions/6594/o1kong-jian-by-powcai/