算法学习-广度优先遍历(单源BFS、多源BFS、双向BFS)
文章目录
- 基础知识
-
- 相关模板
- 多源BFS
- 双向BFS
- 相关题目
-
- 图相关
-
-
- 1162.地图分析
- 934.最短的桥
- 2385.感染二叉树需要的总时间
- 310.最小高度树
- 2359.找到离给定两个节点最近的节点
- 542.01矩阵
- 864.获取所有钥匙的最短路径
-
- 树相关
-
-
- 43.往完全二叉树添加节点
- 44.二叉树每层的最大值
- 45.二叉树最底层最左边的值
- 46.二叉树的右侧视图
-
- 二维平面上的搜索问题
- 抽象成广度优先搜索
-
-
- 127.单词接龙
- 752.打开转盘锁
-
- 多源BFS
-
-
- 1162.地图分析
- 934.最短的桥
- 542.01矩阵
-
- 双向BFS
-
-
- 127.单词接龙
- 752.打开转盘锁
-
广度优先遍历和深度优先遍历是图论中两大重要的算法,但是他们并不是只用于图,在树以及其他题目中都有重要的应用,因此我觉得值得笔者好好进行总结。
参考文献:
负雪明烛大佬的模板
甜姨就图BFS和树DFS的分析
负雪明烛BFS和DFS的区别
liweiwei的BFS、双向BFS
基础知识
BFS常用于从一个点出发求「最短距离」的题目,适用于无权有向图,可以有环,其与DFS的区别如下所示:
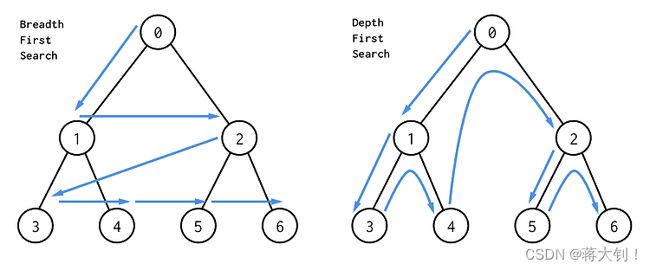
这种无权的最短路算法需要和其他加权有向图的最短路算法进行区分,参考我的另一篇文章算法学习-最短路算法与各种存图方式。
相关模板
BFS使用队列,先将出发点放入队列中,然后从队列中弹出元素往下层访问,直至队列为空,或者有满足条件的答案直接中间return返回。
其中要注意避免重复访问,用标记数组、set或者直接修改元素值来防止重复访问,容易忽略的点是,刚开始加入que的那一个或多个元素,要么本身就已经通过自己的值表示自己已经是被访问过了(如模板),要么就需要额外再用访问数组进行标记(如310.最小高度树)。
模板一.和搜索的层数无关:
只需要一层层访问,不需要记录层数,那么就不需要严格控制一层的元素全部出队列。拓扑排序中可以看到这样的例子。
//单源BFS进一个,多源BFS进多个,默认标记访问
queue.offer(firstnode)
vis[firstnode]=true;
while queue 不空:
cur = queue.pop()
for cur 的所有相邻节点node:
// 先排除无效节点
if node 越界||已访问:
continue;
主逻辑处理
//进入队列标记访问
vis[node]=true;
queue.push(node)
上面的模板是在进入队列的时候就将节点标记为已访问,因此弹出节点已经被标记为访问了。许多大神还是建议在进队的时候就进行标记,可以避免不必要的麻烦。
当然也有在弹出后才标记访问的方法
模板二. 和搜索的层数有关:
这里需要将一层的元素一视同仁,size 表示在当前遍历层有多少个元素,也就是队列中的元素数,我们需要把这些元素一次性遍历完,即把当前层的所有元素都向外走了一步。
这里增加了 level 表示当前遍历到二叉树中的哪一层了,也可以理解为在一个图中,现在已经走了多少步了。level初始化为-1,已经入队的元素弹出才到0,直到最后一个元素弹出,就是已经走的所有元素的层数。
求最短距离的时候,可以在主逻辑处理中,直接return答案。在各种题目中,level需要灵活初始化为0或1,关键在于进队前就需要记录结果,还是出队的时候才记录结果,以及记录的结果是否把路径的两个端点都要算入,因为当轮到出队的时候,这一轮的level已经++了。
//单源BFS进一个,多源BFS进多个,默认标记访问
queue.offer(firstnode)
vis[firstnode]=true;
level = -1
while queue 不空:
level ++;
size = queue.size()
while (size --) {
cur = queue.pop()
for cur 的所有相邻节点node:
// 先排除无效节点
if node 越界||已访问:
continue;
主逻辑处理,最短距离可以直接return答案
// 标记访问
vis[node]=true;
queue.push(node)
}
在求遍历步数、感染步数的时候可以看到它的例子。
多源BFS
简单地说就是在最开始进队的时候进入多个,在统计和层数相关的问题时,实际上是把第一次进队的多个都一视同仁了,在层数上将它们都看作0。后面需要转换思想,灵活选择合适的节点(0或者1)进队,如542.01矩阵。
//单源BFS进一个,多源BFS进多个,默认标记访问
queue.offer(node)
双向BFS
已知BFS起点和终点的情况下,可以分别从起点和目标顶点(终点)执行广度优先遍历,直到遍历的部分有交集,这样子可以减少从一边开始搜索的时候,随着层数的增加,搜索空间变大的情况。
每次选择从节点数较小的一边开始向外扩散,交替扩散直到出现交集,两边扩散的时候都对一个全局的level 进行++,同时在return时看队列是否出现交集。

相关题目
图相关
1162.地图分析
层数相关的多源BFS+求最短距离最大值。也就是求所有陆地与某个海洋最近距离的最大值,即刚开始会在队列中放入多个陆地,一圈一圈地去遍历海洋。每圈的BFS就记录了当前所有陆地与海洋的最短距离,要找到最大的,我们只需要一直找到que.isEmpty()没有节点可以加入,那个时候distance一定是某个点到出发点的最远距离。这里在入队时就进行有效判断以及访问标记。
class Solution {
public int maxDistance(int[][] grid) {
int[]dx=new int[]{0,1,0,-1};
int[]dy=new int[]{1,0,-1,0};
ArrayDeque<int[]> que=new ArrayDeque<>();
int m=grid.length;
int n=grid[0].length;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]==1){
que.offer(new int[]{i,j});
}
}
}
//全是陆地或者海洋特判
if(que.size()==0||que.size()==m*n) return -1;
//刚开始distance默认为-1,陆地出队的时候+1变为0,最后一个出队也会加一次
// distance已走路径两个端点都算了一遍,所以刚开始取-1抵消一次,最后距离只算一个端点
int distance=-1;
while(!que.isEmpty()){
int size=que.size();
distance++;
while(size-->0){
int[] top=que.poll();
for(int i=0;i<4;i++){
int x=top[0]+dx[i];
int y=top[1]+dy[i];
//入队时进行有效判断
if(x<0||x>=m||y<0||y>=n||grid[x][y]!=0) continue;
//入队进行标记访问
grid[x][y]++;
que.offer(new int[]{x,y});
}
}
}
return distance;
}
}
934.最短的桥
DFS标记图+层数相关的多源BFS,不同于1162.地图分析要找到所有最短路的最大值,这里只需要存在一条最近的桥就可以了,可以在找到和当前值不同的值直接return层数。刚开始多源BFS将一座岛上的层数都看为0,在向外扩张的时候相当于是一层一层往外移动,找到最近的另一座岛上的节点就返回。
class Solution:
def shortestBridge(self, grid: List[List[int]]) -> int:
que=deque()
def dfs(grid,i,j,mark):
if i<0 or i>=len(grid) or j<0 or j>=len(grid[0]):
return
if grid[i][j] != 1:
return
grid[i][j]=mark
que.append((i,j))
dfs(grid,i+1,j,mark)
dfs(grid,i-1,j,mark)
dfs(grid,i,j-1,mark)
dfs(grid,i,j+1,mark)
find=0
for i in range (len(grid)):
for j in range(len(grid[0])):
if grid[i][j]==1 and find==0:
dfs(grid,i,j,2)
find +=1
# BFS 找最短路径
distance =-1
while len(que)!=0:
distance +=1
size = len(que)
for _ in range(size):
top=que.popleft()
dx=[0,1,0,-1]
dy=[1,0,-1,0]
for k in range(4):
i,j=top[0]+dx[k],top[1]+dy[k]
if i<0 or i>=len(grid) or j<0 or j>=len(grid[0]):
continue
if grid[i][j] == 2:
continue
# 直接return 结果,已走路径的两个端点都不算
if grid[i][j] == 1:
return distance
grid[i][j]=2
que.append((i,j))
return distance
2385.感染二叉树需要的总时间
DFS建图+BFS模板二,由于是无向图,而不是从根到叶子节点有方向的树,可能会出现已访问节点被重复访问的可能,所以得做好标记「不要重复访问」,数组标记或者Set标记都可以,这里选择在入队时就标记。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
HashMap<Integer,HashSet<Integer>> map;
public int amountOfTime(TreeNode root, int start) {
map=new HashMap<>();
buildGraph(root);
HashSet<Integer> vis=new HashSet<>();
Deque<Integer> que=new ArrayDeque<>();
que.offer(start);
vis.add(start);
int res=-1;
while(!que.isEmpty()){
res++;
int size=que.size();
for(int i=0;i<size;i++){
int top=que.poll();
HashSet<Integer>set=map.get(top);
if(set==null) continue;
for(int node:set){
//不重复访问
if(vis.contains(node)) continue;
vis.add(node);
que.offer(node);
}
}
}
return res;
}
public void buildGraph(TreeNode root){
if(root==null) return;
if(root.left!=null){
HashSet<Integer> set1=map.getOrDefault(root.val,new HashSet<Integer>());
HashSet<Integer> set2=map.getOrDefault(root.left.val,new HashSet<Integer>());
set1.add(root.left.val);
set2.add(root.val);
map.put(root.val,set1);
map.put(root.left.val,set2);
}
if(root.right!=null){
HashSet<Integer> set1=map.getOrDefault(root.val,new HashSet<Integer>());
HashSet<Integer> set2=map.getOrDefault(root.right.val,new HashSet<Integer>());
set1.add(root.right.val);
set2.add(root.val);
map.put(root.val,set1);
map.put(root.right.val,set2);
}
buildGraph(root.left);
buildGraph(root.right);
}
}
310.最小高度树
容器并统计入度信息建立无向图+多源BFS模板一,只需要找到最小高度树的节点,而不需要求出最小高度。可以观察到,从叶子节点往里找,可以找到最小高度树,只需要记录最后一轮BFS的节点就是最小高度树的根节点。建图过程中统计了入度信息,不用额外标记访问。
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
//特殊判断一个节点
if(n==1) return Arrays.asList(0);
//容器建立无向图邻接图
HashSet<Integer>[] map=new HashSet[n];
int[] inDegree=new int[n];
for(int i=0;i<n;i++){
map[i]=new HashSet<Integer>();
}
//建立无向图,两个节点都有一个度
for(int[]e:edges){
map[e[0]].add(e[1]);
map[e[1]].add(e[0]);
inDegree[e[0]]++;
inDegree[e[1]]++;
}
Deque<Integer> que=new ArrayDeque<>();
//无向图只有一个度入队
for(int i=0;i<n;i++){
if(inDegree[i]==1) que.offer(i);
}
//记录下最后一圈出队列的数字就是根
ArrayList<Integer> ans=new ArrayList<>();
while(!que.isEmpty()){
ans.clear();
int size=que.size();
for(int i=0;i<size;i++){
int top=que.poll();
ans.add(top);
for(int node:map[top]){
if(--inDegree[node]==1) que.offer(node);
}
}
}
return ans;
}
}
2359.找到离给定两个节点最近的节点
无权图有环,可以尝试BFS求最短路算法,而不用小题大做用其他有权图算法。采用距离数组-1做访问判断,距离按圈数增加+1。
class Solution {
public int closestMeetingNode(int[] edges, int node1, int node2) {
int len=edges.length;
int[] dis1=new int[len];
int[] dis2=new int[len];
Arrays.fill(dis1,-1);
Arrays.fill(dis2,-1);
bfs(node1,edges,dis1);
bfs(node2,edges,dis2);
int minDis=len;
int index=-1;
for(int i=0;i<len;i++){
if(dis1[i]==-1||dis2[i]==-1) continue;
int maxD=Math.max(dis1[i],dis2[i]);
if(maxD<minDis){
minDis=maxD;
index=i;
}
}
return index;
}
public void bfs(int node,int[]edges,int[]dis){
ArrayDeque<Integer> que=new ArrayDeque<>();
que.offer(node);
dis[node]=0;
int cur=0;
while(!que.isEmpty()){
int size=que.size();
cur++;
for(int i=0;i<size;i++){
int top=que.poll();
if(edges[top]!=-1&&dis[edges[top]]==-1){
dis[edges[top]]=cur;
que.offer(edges[top]);
}
}
}
}
}
这道题目给的是内向基环树,可以采用一个循环求最短路径的方法,
class Solution {
public int closestMeetingNode(int[] edges, int node1, int node2) {
int len=edges.length;
int[] dis1=new int[len];
int[] dis2=new int[len];
Arrays.fill(dis1,-1);
Arrays.fill(dis2,-1);
bfs(node1,edges,dis1);
bfs(node2,edges,dis2);
int minDis=len;
//不存在返回-1
int index=-1;
for(int i=0;i<len;i++){
if(dis1[i]==-1||dis2[i]==-1) continue;
int maxD=Math.max(dis1[i],dis2[i]);
if(maxD<minDis){
minDis=maxD;
index=i;
}
}
return index;
}
public void bfs(int node,int[]edges,int[]dis){
//在不是最后一个点以及有环的情况下一直算dis
for(int d=0;node!=-1&&dis[node]==-1;node=edges[node]){
dis[node]=d++;
}
}
}
542.01矩阵
和层数相关的多源BFS,求1到0的最近距离,这里转换思想,将所有0一视同仁,反而求所有0到最近的1的距离。distance初始化为0,因为节点在进队前就判断是否为1赋值了,已走路径只算了一个端点。
class Solution:
def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
q=deque()
res=[[0]*len(mat[0]) for _ in range(len(mat))]
for i in range(len(mat)):
for j in range(len(mat[0])):
if mat[i][j]==0:
mat[i][j]=-1
q.append((i,j))
#初始化为0,是因为后面进队之前就赋值了
distance=0
while q:
size=len(q)
distance +=1
for i in range(size):
top= q.popleft()
topx=top[0]
topy=top[1]
dx=[0,1,0,-1]
dy=[1,0,-1,0]
for k in range(4):
x=topx+dx[k]
y=topy+dy[k]
if x<0 or x>=len(mat) or y<0 or y>=len(mat[0]) or mat[x][y]==-1:
continue
# 进队之前就赋值
if mat[x][y]==1:
res[x][y]=distance
mat[x][y]=-1
q.append((x,y))
return res
864.获取所有钥匙的最短路径
和层数有关的单源BFS+状态压缩。通过BFS找最短距离,节点在进入队列的时候,拥有(nx,ny,pnewstatus)坐标x,坐标y和当前已经有的钥匙pnewstatus,通过位运算状态压缩的方法记录手上已经有的钥匙,在拓展节点的时候,需要根据拓展节点的性质能否开锁看是否需要加入队列,如果有新的钥匙则需要改变原来的状态,否则都是旧的钥匙状态延续下去。这里在加入节点的时候,可以前面先将所有不符合条件的节点排除,最后再加入未被访问过的节点。
class Solution:
def shortestPathAllKeys(self, grid: List[str]) -> int:
q=deque()
vis=set()
dir=[(0,1),(0,-1),(1,0),(-1,0)]
n,m,cnt=len(grid),len(grid[0]),0
for i in range(n):
for j in range(m):
if grid[i][j]=='@':
q.append((i,j,0))
vis.add((i,j,0))
if 'a'<=grid[i][j]<='z':
cnt +=1
level=0
while q:
level +=1
size = len(q)
for _ in range(size):
top=q.popleft()
px,py,pstatus=top[0],top[1],top[2]
for d in range(len(dir)):
nx=px+dir[d][0]
ny=py+dir[d][1]
if nx<0 or nx>=n or ny<0 or ny>=m:
continue
# 记录下一步的状态
pnewstatus=pstatus
c=grid[nx][ny]
if c=='#':
continue
if 'A'<=c<='Z' and pstatus>>(ord(c)-ord('A'))&1==0:
continue
if 'a'<=c<='z':
pnewstatus=pstatus|1<<(ord(c)-ord('a'))
# 所有连续的钥匙都已经找到
if (1<<cnt)-1==pnewstatus:
return level
# 最后将符合搜索条件的节点加入队列中
if (nx,ny,pnewstatus) not in vis:
q.append((nx,ny,pnewstatus))
vis.add((nx,ny,pnewstatus))
return -1
树相关
43.往完全二叉树添加节点
采用和搜索层数无关的广度优先搜索,找到某个节点的左节点或者右节点为空,则将新节点插入到其左节点或者右节点上。后面的查询可以从该点开始查,不需要每次重新入队,将前面已经出队列的点再入队一次,因此可以将该点放入队头。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class CBTInserter {
TreeNode root;
ArrayDeque<TreeNode> que;
public CBTInserter(TreeNode _root) {
root=_root;
que=new ArrayDeque<>();
}
public int insert(int v) {
TreeNode newNode=new TreeNode(v);
que.offer(root);
while(!que.isEmpty()){
TreeNode top=que.poll();
if(top.left==null){
top.left=newNode;
que.offerFirst(top);
}else if(top.right==null){
top.right=newNode;
que.offerFirst(top);
}else{
que.offer(top.left);
que.offer(top.right);
continue;
}
return top.val;
}
return -1;
}
public TreeNode get_root() {
return root;
}
}
/**
* Your CBTInserter object will be instantiated and called as such:
* CBTInserter obj = new CBTInserter(root);
* int param_1 = obj.insert(v);
* TreeNode param_2 = obj.get_root();
*/
44.二叉树每层的最大值
经典层序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> largestValues(TreeNode root) {
ArrayList<Integer> ans=new ArrayList<>();
if(root==null) return ans;
Deque<TreeNode> que=new LinkedList<>();
que.offer(root);
while(!que.isEmpty()){
int size=que.size();
int maxV=Integer.MIN_VALUE;
for(int i=0;i<size;i++){
TreeNode top=que.poll();
maxV=Math.max(maxV,top.val);
if(top.left!=null) que.offer(top.left);
if(top.right!=null) que.offer(top.right);
}
ans.add(maxV);
}
return ans;
}
}
45.二叉树最底层最左边的值
同样是层次遍历,记录最后一层最左边的数字,只需要用一个局部变量ans每次都更新为最左边的数字,最后就是最后一层最左边的数字。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int findBottomLeftValue(TreeNode root) {
Deque<TreeNode> que=new ArrayDeque<>();
que.offer(root);
int ans=-1;
while(!que.isEmpty()){
int size=que.size();
for(int i=0;i<size;i++){
TreeNode top=que.poll();
if(i==0) ans=top.val;
if(top.left!=null) que.offer(top.left);
if(top.right!=null) que.offer(top.right);
}
}
return ans;
}
}
46.二叉树的右侧视图
经典层次遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> rightSideView(TreeNode root) {
Deque<TreeNode> que=new ArrayDeque<>();
ArrayList<Integer> ans=new ArrayList<>();
if(root==null) return ans;
que.offer(root);
while(!que.isEmpty()){
int size=que.size();
for(int i=0;i<size;i++){
TreeNode top=que.poll();
if(i==size-1) ans.add(top.val);
if(top.left!=null) que.offer(top.left);
if(top.right!=null) que.offer(top.right);
}
}
return ans;
}
}
二维平面上的搜索问题
这个类型的题目我在我的另一篇文章算法学习-深度优先遍历也进行了总结,有些题目广度优先遍历也可以解答。
抽象成广度优先搜索
127.单词接龙
层数相关的BFS+求最短距离。将单词的改变序列抽象为BFS一层层地扩散,扩散的机制为只改变原序列的一个字母并且改变后的字母在wordList中,先用哈希表将wordList单词存起来,通过对单词一位的26个字母不断枚举,判断新的单词是否在该哈希表中,如果不存在则忽略,如果存在则看其是否为最终单词。在这个过程中用set标记已经被访问过的单词,防止有环形成重复访问。这题起点和终点都确定,也可以用双向BFS解答。
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
wordset=set(wordList)
# 合法的单词序列
if beginWord in wordset:
wordset.remove(beginWord)
q=deque()
vis=set()
q.append(beginWord)
vis.add(beginWord)
level=0
while q:
level +=1
size=len(q)
# 针对每个单词
for _ in range(size):
top=q.popleft()
# 枚举其每一位上26个字母的可能性
listword=list(top)
for i,c in enumerate(top):
for k in range(26):
listword[i]=chr(ord('a')+k)
nextword=''.join(listword)
# 在合法的单词序列中
if nextword in wordset:
# 下一个单词就是终点词
if nextword == endWord:
return level+1
# 下一个单词不是终点次且没有被访问
if nextword not in vis:
vis.add(nextword)
q.append(nextword)
# 将当前被替换位复原
listword[i]=c
return 0
752.打开转盘锁
类似127.单词接龙,这里有需要在deadends以外的情况中选择,同时每次只能旋转一次+1,-1改变一次。需要考虑更多的特殊情况,beginword可能就是endword,beginword可能就在dendends中。
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
# 特殊情况考虑
if '0000'in deadends:
return -1
if '0000' == target:
return 0
deadset=set(deadends)
q=collections.deque()
vis=set()
vis.add('0000')
q.append('0000')
level=-1
while q:
level +=1
size=len(q)
# 所有可行元素逐层出队
for _ in range(size):
top=q.popleft()
listword=list(top)
# 针对一个word的所有位置上的元素
for i,c in enumerate(listword):
# 该位置上的两种情况枚举
for k in {1,-1}:
listword[i]=str((int(c)+k+10)%10)
nextword=''.join(listword)
# 当nextword不在deadset中时
if nextword not in deadset:
if nextword==target:
return level +1
if nextword not in vis:
q.append(nextword)
vis.add(nextword)
# 回溯还原,避免对下一次枚举产生影响
listword[i]=c
return -1
多源BFS
1162.地图分析
层数相关的多源BFS+求最短距离最大值。也就是求所有陆地与某个海洋最近距离的最大值,即刚开始会在队列中放入多个陆地,一圈一圈地去遍历海洋。每圈的BFS就记录了当前所有陆地与海洋的最短距离,要找到最大的,我们只需要一直找到que.isEmpty()没有节点可以加入,那个时候distance一定是某个点到出发点的最远距离。这里在入队时就进行有效判断以及访问标记。
class Solution {
public int maxDistance(int[][] grid) {
int[]dx=new int[]{0,1,0,-1};
int[]dy=new int[]{1,0,-1,0};
ArrayDeque<int[]> que=new ArrayDeque<>();
int m=grid.length;
int n=grid[0].length;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]==1){
que.offer(new int[]{i,j});
}
}
}
//全是陆地或者海洋特判
if(que.size()==0||que.size()==m*n) return -1;
//刚开始distance默认为-1,陆地出队的时候+1变为0
int distance=-1;
while(!que.isEmpty()){
int size=que.size();
distance++;
while(size-->0){
int[] top=que.poll();
for(int i=0;i<4;i++){
int x=top[0]+dx[i];
int y=top[1]+dy[i];
if(x<0||x>=m||y<0||y>=n||grid[x][y]!=0) continue;
//标记为已访问
grid[x][y]++;
que.offer(new int[]{x,y});
}
}
}
return distance;
}
}
934.最短的桥
DFS标记图+层数相关的多源BFS,不同于1162.地图分析要找到所有最短路的最大值,这里只需要存在一条最近的桥就可以了,可以在找到和当前值不同的值直接return层数。刚开始多源BFS将一座岛上的层数都看为0,在向外扩张的时候相当于是一层一层往外移动,找到最近的另一座岛上的节点就返回。
class Solution:
def shortestBridge(self, grid: List[List[int]]) -> int:
que=deque()
def dfs(grid,i,j,mark):
if i<0 or i>=len(grid) or j<0 or j>=len(grid[0]):
return
if grid[i][j] != 1:
return
grid[i][j]=mark
que.append((i,j))
dfs(grid,i+1,j,mark)
dfs(grid,i-1,j,mark)
dfs(grid,i,j-1,mark)
dfs(grid,i,j+1,mark)
find=0
for i in range (len(grid)):
for j in range(len(grid[0])):
if grid[i][j]==1 and find==0:
dfs(grid,i,j,2)
find +=1
# BFS 找最短路径
distance =-1
while len(que)!=0:
distance +=1
size = len(que)
for _ in range(size):
top=que.popleft()
dx=[0,1,0,-1]
dy=[1,0,-1,0]
for k in range(4):
i,j=top[0]+dx[k],top[1]+dy[k]
if i<0 or i>=len(grid) or j<0 or j>=len(grid[0]):
continue
if grid[i][j] == 2:
continue
# 直接return 结果,已走路径的两个端点都不算
if grid[i][j] == 1:
return distance
grid[i][j]=2
que.append((i,j))
return distance
542.01矩阵
和层数相关的多源BFS,求1到0的最近距离,这里转换思想,将所有0一视同仁,反而求所有0到最近的1的距离。distance初始化为0,因为节点在进队前就判断是否为1赋值了,已走路径只算了一个端点。
class Solution:
def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
q=deque()
res=[[0]*len(mat[0]) for _ in range(len(mat))]
for i in range(len(mat)):
for j in range(len(mat[0])):
if mat[i][j]==0:
mat[i][j]=-1
q.append((i,j))
#初始化为0,是因为后面进队之前就赋值了
distance=0
while q:
size=len(q)
distance +=1
for i in range(size):
top= q.popleft()
topx=top[0]
topy=top[1]
dx=[0,1,0,-1]
dy=[1,0,-1,0]
for k in range(4):
x=topx+dx[k]
y=topy+dy[k]
if x<0 or x>=len(mat) or y<0 or y>=len(mat[0]) or mat[x][y]==-1:
continue
# 进队之前就赋值
if mat[x][y]==1:
res[x][y]=distance
mat[x][y]=-1
q.append((x,y))
return res
双向BFS
127.单词接龙
上面的解法就是用单向的,在起点和终点都知道的情况下,我们用双向BFS作为第二解法。相比于单向在判断return的时候,是看访问队列是否出现交集if nextword in q2
class Solution:
def ladderLength(self, beginWord: str, endWord: str, wordList: List[str]) -> int:
wordset=set(wordList)
# 合法的单词序列
if beginWord in wordset:
wordset.remove(beginWord)
# 如果endWord没有出现在合法的单词序列中
if endWord not in wordset:
return 0
q1=deque()
vis1=set()
q1.append(beginWord)
vis1.add(beginWord)
q2=deque()
vis2=set()
q2.append(endWord)
vis2.add(endWord)
level=0
while q1 and q2:
if len(q1)>len(q2):
temp1=q1
temp2=vis1
q1=q2
vis1=vis2
q2=temp1
vis2=temp2
level +=1
size=len(q1)
# 针对每个单词
for _ in range(size):
top=q1.popleft()
# 枚举其每一位上26个字母的可能性
listword=list(top)
for i,c in enumerate(top):
for k in range(26):
listword[i]=chr(ord('a')+k)
nextword=''.join(listword)
# 在合法的单词序列中
if nextword in wordset:
# 下一个单词出现交集
if nextword in q2:
return level+1
# 下一个单词没有交集且没有被访问
if nextword not in vis1:
vis1.add(nextword)
q1.append(nextword)
# 将当前被替换位复原
listword[i]=c
return 0
752.打开转盘锁
上面的解法是单向的,尝试用双向BFS进行解答.
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
# 特殊情况考虑
if '0000'in deadends:
return -1
if '0000' == target:
return 0
deadset=set(deadends)
q1=collections.deque()
vis1=set()
vis1.add('0000')
q1.append('0000')
q2=collections.deque()
vis2=set()
vis2.add(target)
q2.append(target)
level=-1
while q1 and q2:
level +=1
if len(q1)>len(q2):
temp1=q1
q1=q2
q2=temp1
temp2=vis1
vis1=vis2
vis2=temp2
size=len(q1)
# 所有可行元素逐层出队
for _ in range(size):
top=q1.popleft()
listword=list(top)
# 针对一个word的所有位置上的元素
for i,c in enumerate(listword):
# 该位置上的两种情况枚举
for k in {1,-1}:
listword[i]=str((int(c)+k+10)%10)
nextword=''.join(listword)
# 当nextword不在deadset中时
if nextword not in deadset:
# nextword在下面出现交集
if nextword in q2:
return level +1
if nextword not in vis1:
q1.append(nextword)
vis1.add(nextword)
# 回溯还原,避免对下一次枚举产生影响
listword[i]=c
return -1