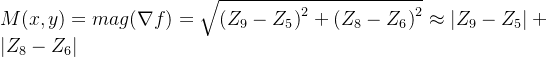数字图像处理第三章-----空间域滤波

目录

一：区分卷积和相关

二：滤波器的种类

2.1 平滑空间滤波

2.1.1 平滑的线性滤波器

2.1.2 统计排序(非线性)滤波器

2.2 锐化空间滤波

2.2.1使用二阶微分锐化图像——拉普拉斯算子（线性）

2.2.2非锐化掩蔽和高提升滤波

2.2.3 使用一阶微分锐化（非线性）图像——梯度

一：区分卷积和相关

        图像处理中常常需要用一个滤波器做空间滤波操作。空间滤波操作有时候也被叫做卷积滤波，或者干脆叫卷积（离散的卷积，不是微积分里连续的卷积）；滤波器也有很多名字：卷积模版、卷积核、掩模、窗口等。

        空间滤波也可以分为线性滤波和非线性滤波。非线性滤波常见的有中值滤波、最大值滤波等，相当于自定义一个函数，在数学上由于不满足线性变换因此叫做非线性滤波。

        线性滤波则通常是：将模版覆盖区域内的元素，以模版中对应位置元素为权值，进行累加。看起来挺简单的，但是要区分相关(cross-correlation)和卷积(convolution)两种模式。

我们最容易的理解是：

相关：从左向右，从上到下，逐个元素乘积再求和

卷积：将模板反转180度，然后执行相关操作。这和卷积神经网络说的不同。

        当然，如果模版是180°对称的那么卷积和相关是相同的。但是并不是所有的模版都对称。因此，在滑窗操作、计算图像梯度等场合，不要使用“卷积”，而要使用“滤波”或者“相关”。因为，我们通常讲的卷积，其实是相关，那就不要用卷积这个词以免引起混淆。

二：滤波器的种类

空间域滤波大体分为两类：平滑空间滤波、锐化空间滤波。

2.1 平滑空间滤波

        对像素点领域的像素值施于某种算法，以其结果替代当前像素点对应的像素值。平滑空间滤波器常用于模糊处理和降低噪声。模糊处理常用于预处理任务中，比如在（大）目标提取之前去除图像中的一些琐碎的细节，以及连接直线或曲线的缝隙。通过线性和非线性滤波模糊处理，可以降低噪声。平滑的空间滤波器分为：平滑的线性滤波器和基于统计排序(非线性)滤波器。

2.1.1 平滑的线性滤波器

（1）算术均值滤波

        最简单的均值滤波器，计算公式如下：

         表示的是中心点在处，大小为m×n的矩形图像区域的一组坐标，表示均值处理之后点(x,y)处的像素值。表示这个区域里面的像素值。算术均值滤波其实就是计算区域的平均值，用平均值代替当前点的像素值。

（2）几何均值滤波

         几何均值滤波其实就是计算区域内像素值的乘积的幂。几何均值滤波器实现的平滑相比于算术均值滤波器丢失的图像细节更少。

（3）谐波均值滤波

        

        谐波均值滤波是用mn除以区域内像素值取倒数的和，谐波均值滤波对于盐粒噪声效果比较好，但不适用于胡椒噪声，也利于处理高斯噪声，因为椒盐噪声对应黑白相间的亮暗点，椒对应黑（像素值比较小，黑色的像素值是0），盐对应白（像素值比较大，白色的像素值是255），如果是胡椒噪声，的值比较大，那么求和之后整体的值是比较小的，那么整个滤波之后的像素接近于0，无法识别。

（4）逆谐波均值滤波

        

        其中Q称为滤波器的阶数。这种滤波器适合减少或在实际中消除椒盐噪声的影响。当Q为正值时，该滤波器消除胡椒噪声，当Q值为负时，该滤波器消除盐粒噪声。但它不能同时消除两种噪声。当Q=0时，逆谐波滤均值波器简化为算术均值滤波器。当Q=-1时，转化为谐波均值滤波器。

2.1.2 统计排序(非线性)滤波器

        统计排序滤波器时空间滤波器，空间滤波器的响应基于该滤波器周围的图像区域中的像素值排序，排序的结果决定滤波器的响应。

（1）中值滤波

它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值，也就是将中心像素的值用所有像素值的中间值（不是平均值）替换。中值滤波通过选择中间值避免图像孤立噪声点的影响，对脉冲噪声、斑点噪声、椒盐噪声有良好的滤除作用，特别是在滤除噪声的同时，能够保护信号的边缘，使之不被模糊。这些优良特性是线性滤波方法所不具有的。

（2）最大值和最小值滤波

         对区域内像素点排序，选着最大值的像素值作为最终结果，因此最大值滤波器对于发现图像中的最亮点非常有用。同样因为胡椒噪声的值非常的低，所以最大值滤波器可以降低胡椒噪声。

        对区域内像素点排序，选着最小值的像素值作为最终结果，因此最小值滤波器对于发现图像中的最暗点非常有用。同样因为盐粒噪声的值非常的低，所以最小值滤波器可以降低盐粒噪声。

（3）中点滤波

 该滤波器计算包围在滤波器区域内像素最大值和最小值的中点。

（4）修正的阿尔法均值滤波器

        修正的阿尔法均值滤波器类似于去掉最高分与去掉最低分评价一个选手水平的方法，即将滤波范围内的数据进行排序，从大到小的顺序去除d/2个数据，从小到大的顺序去除d/2个数据，将剩下的数据计算均值。这样的滤波器，很擅长去除椒盐噪声和其他类型噪声一起污染过的图片。如果d=mn-1，则修正的阿尔法均值滤波器转化为了中值滤波器了。当d=0，修正的阿尔法均值滤波器变为了算术均值滤波器了。

2.2 锐化空间滤波

        锐化处理的主要目的是突出灰度的过渡部分，补偿图像的轮廓，增强图像的边缘及灰度跳变的部分，使图像变得清晰。图像锐化的用途多种多样，应用范围从电子印刷和医学成像到工业检测和军事系统的制导等。图像的模糊可以通过积分来实现（均值处理与积分类似）。而图像锐化，则需要微分来实现。图像的模糊主要通过积分来实现（均值与积分类似），而图像的锐化处理可由空间微分来实现。本文主要介绍3中方法：拉普拉斯算子（二阶微分）、非锐化掩蔽、一阶微分（包括罗伯特交叉梯度算子和Soble算子）

下面的内容，我们将先讨论由数字微分来定义和实现锐化算子的方法
一维函数的一阶微分基本定义是差值:

 一维函数的二阶微分的定义为差分： 

由于图像有ｘ和ｙ两个方向，因此图像信号属于二维离散信号。其在ｘ,ｙ两个方向的离散二阶微分公式如下： 

 一阶微分的性质：

（1）在恒定的灰度区域，图像的微分值为0.（灰度值没有发生变换，自然微分为0）

（2）在灰度台阶或斜坡起点处微分值不为0.（台阶是，灰度值的突变变化较大；斜坡则是灰度值变化较缓慢；灰度值发生了变化，微分值不为0）

（3）沿着斜坡的微分值不为0

二阶微分的性质：（是一阶微分的导数，和一阶微分相对应）

 （1）在恒定区域二阶微分值为0

（2）在灰度台阶或斜坡的起点处微分值不为0；

（3）沿着斜坡的微分值为0

2.2.1使用二阶微分锐化图像——拉普拉斯算子（线性）

首先，拉普拉斯算子是最简单的各向同性微分算子，它具有旋转不变性。一个二维图像函数的拉普拉斯变换是各向同性的二阶导数(由于二阶微分的性质可知：拉普拉斯算子的应用强调的是图像中灰度的突变，并不强调灰度级缓慢变化的区域)，定义为：

由于图像有和两个方向，因此图像信号属于二维离散信号。其在两个方向的离散二阶微分公式如下： 

另外，拉普拉斯算子还可以表示成模板的形式，以便更好编程需要。如下图所示：

 从左到右依次是：正拉普拉斯算子模板，带对角项的扩展模板，负的拉普拉斯算子模板，负的带对角项的扩展模板。

在正拉普拉斯算子中，我们使用标准掩模，掩模的中心元素应为阴性，掩模的角元素应为零。正拉普拉斯算符用于取出图像中的向外边缘。在负拉普拉斯算符中，我们也有一个标准的掩码，其中的中心元素应该是正的。角落中的所有元素应为零，掩码中所有元素的其余部分应为-1。负拉普拉斯算符用于取出图像中的向内边缘。

因为正拉普拉斯模板具有上下左右四个90度的方向上结果相同，也就是说在90度方向上无方向性。而带对角的扩展目的是为了保证其在上下左右45度的方向上结果相同，也就是说在45度方向上无方向性。

锐化处理可选择拉普拉斯算子对原图像进行处理，产生描述灰度突变的图像，再将拉普拉斯图像与原始图像叠加而产生锐化图像，即锐化图像=原图像+拉普拉斯图像。拉普拉斯锐化的基本方法可以由下式表示：

2.2.2非锐化掩蔽和高提升滤波

非锐化掩蔽的步骤：

1.模糊图像

2.从原始图像中减去模糊图像（产生的差值图像称为模板）

3.将模板加到原图像上

 令表示模糊图像，非锐化掩蔽的公式描述如下：

   此处得到的时非锐化掩蔽的模板。

 然后，在原始图像上加上该模板的一个权重部分：

 其中k>=0,当k=1时，就是我们定义的非锐化掩蔽。当k>1时，该处理称为高提升滤波。

2.2.3 使用一阶微分锐化（非线性）图像——梯度

         图像的一阶微分是采用梯度的幅值来实现的，对于函数,在坐标处的梯度定义为二维列向量：

        

 该向量具有重要的几何特性，即它指出了在位置（x，y）处f的最大变化率的方向。梯度是一个向量，分量分别为坐沿着坐标轴的偏导数。

向量的幅值（长度）表示，即：

实际操作中用绝对值来近似的平方和平方根操作更方便。

（1）Robertes cross(罗伯特交叉)算子

罗伯特在提出两个定义使用交叉差分：

 和 

这一点在是我们前面讨论的一阶微分： 和，是采用交差的形式计算微分。则此时梯度图像为：

因此，罗伯特交叉算子对应的模板是：

（2）Sobel算子 

 Sobel(索贝尔算子)算子是一个离散微分算子 (discrete differentiation operator)。 它结合了高斯平滑和微分求导，用来计算图像灰度函数的近似梯度

       

 因此，Sobel算子对应的模板是：