AcWing算法提高课笔记
目录
Level2
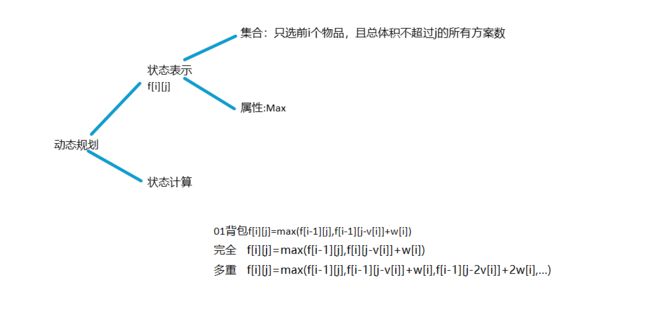
1.动态规划——从集合角度考虑DP问题
1.1 数字三角形模型
1.1.1摘花生
1.1.2最低通行费
1.1.3方格取数
1.1.4传纸条
1.2 最长上升子序列模型
1.2.1怪盗基德的滑翔翼
1.2.2登山
1.2.3合唱队形
1.2.4好友城市
1.2.5最大上升子序列和
1.2.6拦截导弹
1.2.7导弹防御系统
1.2.8最长上升公共子序列
1.3 背包模型
1.3.1采药
1.3.2装箱问题
1.3.3宠物小精灵之收服
1.3.4数字组合
1.3.5买书
1.3.6货币系统
1.3.7货币系统
1.3.8多重背包问题III
1.3.9庆功会
1.3.10混合背包问题
1.3.11二维费用的背包问题
1.3.12潜水员
1.3.13机器分配
1.3.14开心的金明
1.3.15有依赖的背包问题
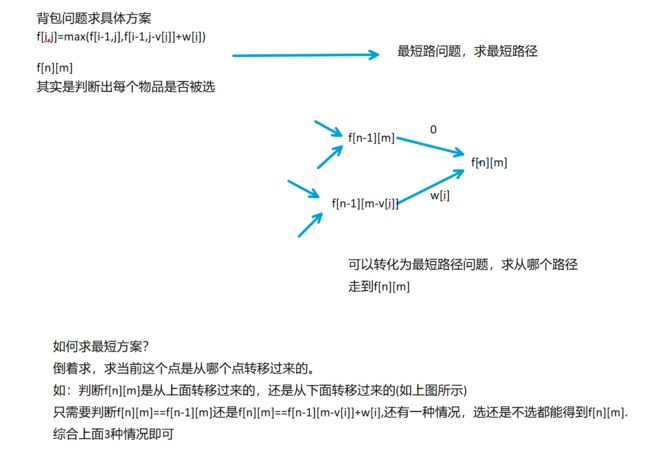
1.3.16背包问题求方案数
1.3.17背包问题求具体方案
1.3.18能量石
1.3.19金明的预算方案
1.4 状态机模型
1.4.1大盗阿福
1.4.2股票买卖IV
1.4.3股票买卖V
1.4.4设计密码
1.4.5修复DNA
1.5 状态压缩DP
1.5.1小国王
1.5.2玉米田
1.5.3炮兵阵地
1.5.4愤怒的小鸟
1.5.5宝藏
1.6 区间DP
1.6.1环形石子合并
1.6.2能量项链
1.6.3加分二叉树
1.6.4凸多边形的划分
1.6.5棋盘分割
1.7 树形DP
1.7.1树的最长路径
1.7.2树的中心
1.7.3数字转换
1.7.4二叉苹果树
1.7.5战略游戏
1.7.6皇宫看守
1.8 数位DP
1.8.1度的数量
1.8.2数字游戏
1.8.3Windy数
1.8.4数字游戏II
1.8.5不要62
1.8.6恨7不成妻
1.9 单调队列优化的DP问题
1.9.1最大子序和
1.9.2修剪草坪
1.9.3旅行问题
1.9.4烽火传递
1.9.5绿色通道
1.9.6理想的正方形
1.10 斜率优化的DP问题
1.10.1任务安排1
1.10.2任务安排2
1.10.3任务安排3
1.10.4运输小猫
2.搜索
BFS
2.1 Flood Fill
2.1.1池塘计数
2.1.2城堡问题
2.1.3山谷和山峰
2.2 最短路模型
2.2.1迷宫问题
2.2.2武士风度的牛
2.2.3抓住那头牛
2.3 多源BFS
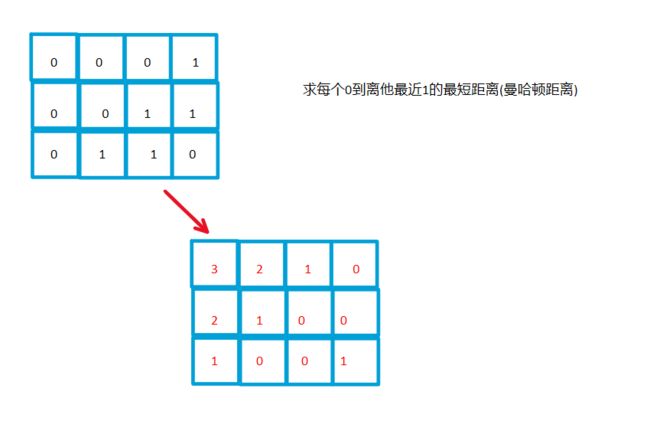
2.3.1矩阵距离
2.4 最小步数模型
2.4.1魔板
2.5 双端队列广搜
2.5.6电路维修
2.6 双向广搜
2.6.1字串变换
2.7 A*
2.7.1第K短路
2.7.2八数码
DFS
2.8DFS 之连通性模型
2.8.1迷宫
2.8.2红与黑
2.9DFS 之搜索顺序
2.9.1马走日
2.9.2单词接龙
2.9.3分成互质组
2.10DFS之剪枝与优化
2.10.1小猫爬山
2.10.2数独
2.10.3木棒
2.10.4生日蛋糕
2.11 迭代加深
2.11.1加成序列
2.12 双向DFS
2.12.1送礼物
2.13 IDA*
2.13.1排书
2.13.2回转游戏
3.图论
3.1单源最短路的建图方式
3.1.1热浪
【题目描述】
【输入】
【输出】
【输入样例】
【输出样例】
【提示】
3.1.2信使
【题目描述】
【输入】
【输出】
【输入样例】
【输出样例】
3.2 单源最短路的综合应用
3.3 单源最短路的扩展应用
3.4 floyd算法及其变形
3.5 最小生成树的典型应用
3.6 最小生成树的扩展应用
3.7 SPFA求负环
3.8 差分约束
3.9 最近公共祖先
3.10 有向图的强连通分量
3.11 无向图的双连通分量
3.12 二分图
3.13 欧拉回路和欧拉路径
3.14 拓扑排序
4.高级数据结构
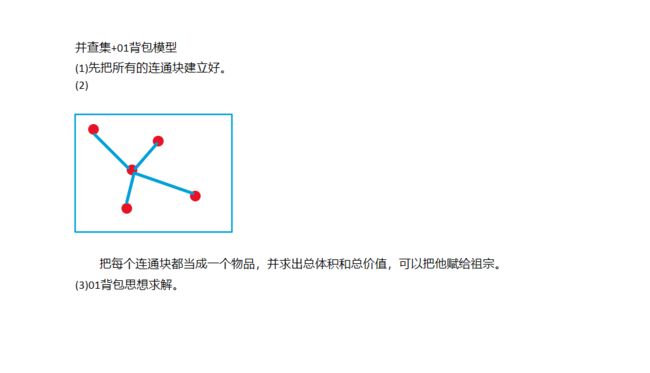
4.1 并查集
4.1.1格子游戏
4.1.2搭配购买
4.1.3程序自动分析
4.1.4奇偶游戏
4.1.5银河英雄传说
4.2 树状数组
4.2.1楼兰图腾
4.2.2一个简单的整数问题
4.2.3一个简单的整数问题2
4.2.4谜一样的牛
4.3线段树
4.3.0动态区间求连续和
4.3.1最大数
4.3.2你能回答这些问题吗
4.3.3区间最大公约数
4.3.4一个简单的整数问题2
4.3.5亚特兰蒂斯
4.3.6维护序列
4.4 可持久化数据结构
4.4.1最大异或和
4.4.2第K小数
4.5 平衡树——Treap
4.5.1普通平衡树
4.5.2营业额统计
4.6 AC自动机
4.6.1搜索关键词
4.6.2单词
5.数学知识
5.1 筛质数
5.2 分解质因数
5.3 快速幂
5.4 约数个数
5.5 欧拉函数
5.6 同余
5.7 矩阵乘法
5.8 组合计数
5.9 高斯消元
5.10 容斥原理
5.11 概率与数学期望
5.12 博弈论
6.基础算法
6.1 位运算
6.1.1 64位整数乘法
6.2 递归
6.2.1费解的开关
6.2.2约数之和
6.2.3分形之城
6.3 前缀和与差分
6.3.1激光炸弹
6.3.2增减序列
6.4 二分
6.4.1最佳牛围栏
6.4.2特殊排序
6.5 排序
6.5.1七夕祭
6.5.2动态中位数
6.5.3超快速排序
6.6 RMQ
6.6.1天才的记忆
Level2
1.动态规划——从集合角度考虑DP问题
1.1 数字三角形模型
1.1.1摘花生
Hello Kitty想摘点花生送给她喜欢的米老鼠。
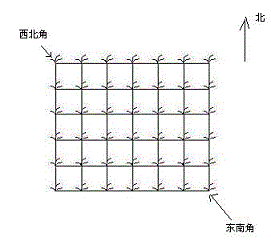
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1≤T≤100,
1≤R,C≤100,
0≤M≤1000
输入样例:
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例:
8
16
思路
#include
using namespace std;
const int N = 105;
int a[N][N], f[N][N];
int q, row, col;
int main()
{
cin >> q;
while(q--){
cin >> row >> col;
for(int i = 1; i <= row; i++){
for(int j = 1; j <= col; j++){
cin >> a[i][j];
}
}
// f[i][j]指的是到(i, j)的最大花生数
for(int i = 1; i <= row; i++){
for(int j = 1; j <= col; j++){
f[i][j] = max(f[i-1][j], f[i][j-1]) + a[i][j];
}
}
cout << f[row][col] << endl;
}
return 0;
} 1.1.2最低通行费
一个商人穿过一个 N×N 的正方形的网格,去参加一个非常重要的商务活动。
他要从网格的左上角进,右下角出。
每穿越中间 1 个小方格,都要花费 1 个单位时间。
商人必须在 (2N−1) 个单位时间穿越出去。
而在经过中间的每个小方格时,都需要缴纳一定的费用。
这个商人期望在规定时间内用最少费用穿越出去。
请问至少需要多少费用?
注意:不能对角穿越各个小方格(即,只能向上下左右四个方向移动且不能离开网格)。
输入格式
第一行是一个整数,表示正方形的宽度 N。
后面 N 行,每行 N 个不大于 100 的正整数,为网格上每个小方格的费用。
输出格式
输出一个整数,表示至少需要的费用。
数据范围
1≤N≤100
输入样例:
5
1 4 6 8 10
2 5 7 15 17
6 8 9 18 20
10 11 12 19 21
20 23 25 29 33
输出样例:
109
样例解释
样例中,最小值为 109=1+2+5+7+9+12+19+21+33。
思路
AC代码
#include
#include
#include
using namespace std;
const int N=1100,INF=1e9;
int n;
int w[N][N];
int f[N][N];
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>w[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i==1&&j==1) f[i][j]=w[i][j];
else
{
f[i][j]=INF;
if(i>1) f[i][j]=min(f[i][j],f[i-1][j])+w[i][j];//不是第一行才可以从上面过来
if(j>1) f[i][j]=min(f[i][j],f[i][j-1])+w[i][j];//不是第一列才可以从左边过来
}
cout< 1.1.3方格取数
设有N*N的方格图(N<=10),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。
某人从图的左上角的A 点(1,1)出发,可以向下行走,也可以向右走,直到到达右下角的B点(N,N)。在走过的路上,他可以取走方格中的数(取走后的方格中将变为数字0)。
此人从A点到B 点共走两次,试找出2条这样的路径,使得取得的数之和为最大。
输入格式:
输入的第一行为一个整数N(表示N*N的方格图),接下来的每行有三个整数,前两个表示位置,第三个数为该位置上所放的数。一行单独的0表示输入结束。
输出格式:
只需输出一个整数,表示2条路径上取得的最大的和。
输入样例:
在这里给出一组输入。例如:
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
1
2
3
4
5
6
7
8
9
10
输出样例:
在这里给出相应的输出。例如:
67
#include
#include
#include
#include
using namespace std;
const int N=15;
int n;
int w[N][N];
int f[N*2][N*2][N*2];
int main()
{
cin>>n;
int a,b,c;
while(cin>>a>>b>>c,a||b||c) w[a][b]=c;
for(int k=2;k<=n+n;k++)
for(int i1=1;i1<=n;i1++)
for(int i2=1;i2<=n;i2++)
{
int j1=k-i1,j2=k-i2;
if(j1>=1&&j1<=n&&j2>=1&&j2<=n)
{
int t=w[i1][j1];
if(i1!=i2) t+=w[i2][j2];
int &x=f[k][i1][i2];
x=max(x,f[k-1][i1-1][i2-1]+t);
x=max(x,f[k-1][i1-1][i2]+t);
x=max(x,f[k-1][i1][i2-1]+t);
x=max(x,f[k-1][i1][i2]+t);
}
}
cout< 1.1.4传纸条
1.2 最长上升子序列模型
1.2.1怪盗基德的滑翔翼
【题目描述】
怪盗基德是一个充满传奇色彩的怪盗,专门以珠宝为目标的超级盗窃犯。而他最为突出的地方,就是他每次都能逃脱中村警部的重重围堵,而这也很大程度上是多亏了他随身携带的便于操作的滑翔翼。
有一天,怪盗基德像往常一样偷走了一颗珍贵的钻石,不料却被柯南小朋友识破了伪装,而他的滑翔翼的动力装置也被柯南踢出的足球破坏了。不得已,怪盗基德只能操作受损的滑翔翼逃脱。
假设城市中一共有N幢建筑排成一条线,每幢建筑的高度各不相同。初始时,怪盗基德可以在任何一幢建筑的顶端。他可以选择一个方向逃跑,但是不能中途改变方向(因为中森警部会在后面追击)。因为滑翔翼动力装置受损,他只能往下滑行(即:只能从较高的建筑滑翔到较低的建筑)。他希望尽可能多地经过不同建筑的顶部,这样可以减缓下降时的冲击力,减少受伤的可能性。请问,他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)?
【输入】
输入数据第一行是一个整数K(K<100)
,代表有K
组测试数据。
每组测试数据包含两行:第一行是一个整数N(N<100)
,代表有N幢建筑。第二行包含N个不同的整数,每一个对应一幢建筑的高度h(0 ,按照建筑的排列顺序给出。 【输出】 对于每一组测试数据,输出一行,包含一个整数,代表怪盗基德最多可以经过的建筑数量。 【输入样例】 3 8 300 207 155 299 298 170 158 65 8 65 158 170 298 299 155 207 300 10 2 1 3 4 5 6 7 8 9 10 【输出样例】 6 6 9 思路: 双向的最长上升子序列模型 【题目描述】 五一到了,ACM队组织大家去登山观光,队员们发现山上一个有N个景点,并且决定按照顺序来浏览这些景点,即每次所浏览景点的编号都要大于前一个浏览景点的编号。同时队员们还有另一个登山习惯,就是不连续浏览海拔相同的两个景点,并且一旦开始下山,就不再向上走了。队员们希望在满足上面条件的同时,尽可能多的浏览景点,你能帮他们找出最多可能浏览的景点数么? 【输入】 第一行:N (2 <= N <= 1000) 景点数; 第二行:N个整数,每个景点的海拔。 【输出】 最多能浏览的景点数。 【输入样例】 8 186 186 150 200 160 130 197 220 【输出样例】 4 题解:最长上升子序列 【题目描述】 N位同学站成一排,音乐老师要请其中的(N−K)位同学出列,使得剩下的KK位同学排成合唱队形。 合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2,…,K,他们的身高分别为T1,T2,…,TK,则他们的身高满足T1 你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。 【输入】 输入的第一行是一个整数N(2≤N≤100),表示同学的总数。第二行有n个整数,用空格分隔,第i个整数Ti(130≤Ti≤230)是第i位同学的身高(厘米)。 【输出】 输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。 【输入样例】 8 186 186 150 200 160 130 197 220 【输出样例】 4 思路: 登山问题的变形。 【题目描述】 Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。 每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以避免事故。编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。 【输入】 第1行,一个整数N(1<=N<=5000),表示城市数。 第2行到第n+1行,每行两个整数,中间用1个空格隔开,分别表示南岸和北岸的一对友好城市的坐标。(0<=xi<=10000) 【输出】 仅一行,输出一个整数,表示政府所能批准的最多申请数。 【输入样例】 7 22 4 2 6 10 3 15 12 9 8 17 17 4 2 【输出样例】 4 所以左边最大值,就是上升子序列的最大值。 可以将下面的序列进行排序,排序之后有单调性,那么上面的如果出现交叉,那么有一对城市不合法。 题目描述: 一个数的序列 bi,当 b1 对于给定的一个序列(a1,a2,…,aN),我们可以得到一些上升的子序列(ai1,ai2,…,aiK),这里1≤i1 比如,对于序列(1,7,3,5,9,4,8),有它的一些上升子序列,如(1,7),(3,4,8)等等。 这些子序列中和最大为18,为子序列(1,3,5,9)的和。你的任务,就是对于给定的序列,求出最大上升子序列和。 注意,最长的上升子序列的和不一定是最大的,比如序列(100,1,2,3)的最大上升子序列和为100,而最长上升子序列为(1,2,3)。 输入格式 输入的第一行是序列的长度N。 第二行给出序列中的N个整数,这些整数的取值范围都在0到10000(可能重复)。 输出格式 输出一个整数,表示最大上升子序列和。 数据范围 1≤N≤1000 输入样例: 7 1 7 3 5 9 4 8 输出样例: 18 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。 但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。 某天,雷达捕捉到敌国的导弹来袭。 由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。 输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数,导弹数不超过1000),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。 输入格式 共一行,输入导弹依次飞来的高度。 输出格式 第一行包含一个整数,表示最多能拦截的导弹数。 第二行包含一个整数,表示要拦截所有导弹最少要配备的系统数。 数据范围 雷达给出的高度数据是不大于 30000 的正整数,导弹数不超过1000。 输入样例: 389 207 155 300 299 170 158 65 输出样例: 6 2 思路: 第一问:最长不上升子序列。 第二问:最少用多少个系统才能把导弹拦截住。 g[]数组存的是末尾的数。 我们可以惊奇的发现,这个思路和最长上升子序列II的做法思路相同。 最长上升子序列方案数=最少用多少个非上升子序列可以把整个序列覆盖掉。 时间复杂度O(nlogn) 为了对抗附近恶意国家的威胁,R国更新了他们的导弹防御系统。 一套防御系统的导弹拦截高度要么一直 严格单调 上升要么一直 严格单调 下降。 例如,一套系统先后拦截了高度为 3 和高度为 4 的两发导弹,那么接下来该系统就只能拦截高度大于 4 的导弹。 给定即将袭来的一系列导弹的高度,请你求出至少需要多少套防御系统,就可以将它们全部击落。 Input 多组测试用例。 对于每个测试用例,第一行包含整数 n ( 1 ≤ n ≤ 50 ),表示来袭导弹数量。 第二行包含 n 个不同的整数,表示每个导弹的高度。 当输入测试用例 n = 0 时,表示输入终止,且该用例无需处理。 Output 每个测试用例输出一行:一个整数,表示所需的防御系统数量。 Sample Input 5 3 5 2 4 1 0 Sample Output 2 方法一:记下来一个全局最小值,不断更新。 熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。 小沐沐先让奶牛研究了最长上升子序列,再让他们研究了最长公共子序列,现在又让他们研究最长公共上升子序列了。 小沐沐说,对于两个数列 A和 B,如果它们都包含一段位置不一定连续的数,且数值是严格递增的,那么称这一段数是两个数列的公共上升子序列,而所有的公共上升子序列中最长的就是最长公共上升子序列了。 奶牛半懂不懂,小沐沐要你来告诉奶牛什么是最长公共上升子序列。 不过,只要告诉奶牛它的长度就可以了。 数列 A和 B的长度均不超过3000。 输入格式 第一行包含一个整数 N,表示数列 A,B 的长度。 第二行包含 N个整数,表示数列 A。 第三行包含 N个整数,表示数列 B。 输出格式 输出一个整数,表示最长公共上升子序列的长度。 数据范围 1≤N≤3000,序列中的数字均不超过2^31−1。 输入样例: 4 2 2 1 3 2 1 2 3 输出样例: 2 思路:最长公共子序列+最长上升子序列 未优化的代码 优化的代码1: 优化2(更容易理解) 辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。 为此,他想拜附近最有威望的医师为师。 医师为了判断他的资质,给他出了一个难题。 医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。” 如果你是辰辰,你能完成这个任务吗? 输入格式 输入文件的第一行有两个整数 T和 M,用一个空格隔开,T代表总共能够用来采药的时间,M代表山洞里的草药的数目。 接下来的 M行每行包括两个在 1到100 之间(包括 1和 100)的整数,分别表示采摘某株草药的时间和这株草药的价值。 输出格式 输出文件包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。 数据范围 1≤T≤1000, 1≤M≤100 输入样例: 70 3 71 100 69 1 1 2 输出样例: 3 思路:01背包模型 有一个箱子容量为 V,同时有 n个物品,每个物品有一个体积。 现在从 n个物品中,任取若干个装入箱内(也可以不取),使箱子的剩余空间最小。输出这个最小值。 输入格式 第一行共一个整数 V,表示箱子容量。 第二行共一个整数 n,表示物品总数。 接下来 n行,每行有一个正整数,表示第 i个物品的体积。 输出格式 共一行一个整数,表示箱子最小剩余空间。 输入输出样例 输入 24 6 8 3 12 7 9 7 输出 0 说明 对于100% 数据,满足 0 01背包的变形问题,把价值换成了体积。 【题目描述】 宠物小精灵是一部讲述小智和他的搭档皮卡丘一起冒险的故事。 一天,小智和皮卡丘来到了小精灵狩猎场,里面有很多珍贵的野生宠物小精灵。小智也想收服其中的一些小精灵。然而,野生的小精灵并不那么容易被收服。对于每一个野生小精灵而言,小智可能需要使用很多个精灵球才能收服它,而在收服过程中,野生小精灵也会对皮卡丘造成一定的伤害(从而减少皮卡丘的体力)。当皮卡丘的体力小于等于0时,小智就必须结束狩猎(因为他需要给皮卡丘疗伤),而使得皮卡丘体力小于等于0的野生小精灵也不会被小智收服。当小智的精灵球用完时,狩猎也宣告结束。 我们假设小智遇到野生小精灵时有两个选择:收服它,或者离开它。如果小智选择了收服,那么一定会扔出能够收服该小精灵的精灵球,而皮卡丘也一定会受到相应的伤害;如果选择离开它,那么小智不会损失精灵球,皮卡丘也不会损失体力。 小智的目标有两个:主要目标是收服尽可能多的野生小精灵;如果可以收服的小精灵数量一样,小智希望皮卡丘受到的伤害越小(剩余体力越大),因为他们还要继续冒险。 现在已知小智的精灵球数量和皮卡丘的初始体力,已知每一个小精灵需要的用于收服的精灵球数目和它在被收服过程中会对皮卡丘造成的伤害数目。请问,小智该如何选择收服哪些小精灵以达到他的目标呢? 【输入】 输入数据的第一行包含三个整数:N(0 之后的K行,每一行代表一个野生小精灵,包括两个整数:收服该小精灵需要的精灵球的数量,以及收服过程中对皮卡丘造成的伤害。 【输出】 输出为一行,包含两个整数:C,R,分别表示最多收服C个小精灵,以及收服C个小精灵时皮卡丘的剩余体力值最多为R。 【输入样例】 10 100 5 7 10 2 40 2 50 1 20 4 20 【输出样例】 3 30 【提示】 样例输入2: 10 100 5 8 110 12 10 20 10 5 200 1 110 样例输出2: 0 100 提示: 对于样例输入1:小智选择:(7,10) (2,40) (1,20) 这样小智一共收服了3个小精灵,皮卡丘受到了70点伤害,剩余100-70=30点体力。所以输出3 30。 对于样例输入2:小智一个小精灵都没法收服,皮卡丘也不会收到任何伤害,所以输出0 100。 给定 N个正整数 A1,A2,…,AN,从中选出若干个数,使它们的和为 M,求有多少种选择方案。 输入格式 第一行包含两个整数 N 和 M。 第二行包含 N个整数,表示 A1,A2,…,AN。 输出格式 包含一个整数,表示可选方案数。 数据范围 1≤N≤100, 1≤M≤10000, 1≤Ai≤1000, 答案保证在 int 范围内。 输入样例: 4 4 1 1 2 2 输出样例: 3 思路:01背包求方案数。 二维代码 优化为一维 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 小明手里有n元钱全部用来买书,书的价格为10元,20元,50元,100元。 问小明有多少种买书方案?(每种书可购买多本) 【输入】 一个整数 n,代表总共钱数。(0≤n≤1000) 【输出】 一个整数,代表选择方案种数。 【输入样例】 20 【输出样例】 2 一维优化 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 给你一个n种面值的货币系统,求组成面值为m的货币有多少种方案。 【输入】 第一行为n和m。 【输出】 一行,方案数。 【输入样例】 3 10 //3种面值组成面值为10的方案 1 //面值1 2 //面值2 5 //面值5 【输出样例】 10 //有10种方案 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 6. 多重背包问题 III - AcWing题库 有 N种物品和一个容量是 V的背包。 第 i种物品最多有 si件,每件体积是vi,价值是 wi。 求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。 输入格式 第一行两个整数,N,V (0 接下来有 N行,每行三个整数vi,wi,si,用空格隔开,分别表示第 i种物品的体积、价值和数量。 输出格式 输出一个整数,表示最大价值。 数据范围 0 0 0 提示 本题考查多重背包的单调队列优化方法。 输入样例 4 5 1 2 3 2 4 1 3 4 3 4 5 2 输出样例: 10 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 为了庆贺班级在校运动会上取得全校第一名成绩,班主任决定开一场庆功会,为此拨款购买奖品犒劳运动员。期望拨款金额能购买最大价值的奖品,可以补充他们的精力和体力。 【输入】 第一行二个数n(n≤500)n(n≤500),m(m≤6000)m(m≤6000),其中nn代表希望购买的奖品的种数,mm表示拨款金额。 接下来nn行,每行33个数,vv、ww、ss,分别表示第I种奖品的价格、价值(价格与价值是不同的概念)和能购买的最大数量(买00件到ss件均可),其中v≤100v≤100,w≤1000w≤1000,s≤10s≤10。 【输出】 一行:一个数,表示此次购买能获得的最大的价值(注意!不是价格)。 【输入样例】 5 1000 80 20 4 40 50 9 30 50 7 40 30 6 20 20 1 【输出样例】 1040 经典的多重背包问题,把数据开大一些 二维 一维 7. 混合背包问题 - AcWing题库 有 N 种物品和一个容量是 V 的背包。 物品一共有三类: 第一类物品只能用1次(01背包); 第二类物品可以用无限次(完全背包); 第三类物品最多只能用 si 次(多重背包); 每种体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。 输入格式 第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。 接下来有 N 行,每行三个整数vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。 si=−1 表示第 i 种物品只能用1次; si=0 表示第 i 种物品可以用无限次; si>0 表示第 i 种物品可以使用 si 次; 输出格式 输出一个整数,表示最大价值。 数据范围 0 0 −1≤si≤1000 输入样例 4 5 1 2 -1 2 4 1 3 4 0 4 5 2 输出样例: 8 信息学奥赛一本通(C++版)在线评测系统 【题目描述】 潜水员为了潜水要使用特殊的装备。他有一个带2种气体的气缸:一个为氧气,一个为氮气。让潜水员下潜的深度需要各种的数量的氧和氮。潜水员有一定数量的气缸。每个气缸都有重量和气体容量。潜水员为了完成他的工作需要特定数量的氧和氮。他完成工作所需气缸的总重的最低限度的是多少? 例如:潜水员有5个气缸。每行三个数字为:氧,氮的(升)量和气缸的重量: 3 36 120 10 25 129 5 50 250 1 45 130 4 20 119 如果潜水员需要5升的氧和60升的氮则总重最小为249(1,2或者4,5号气缸)。 你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。 【输入】 第一行有2整数m,n(1≤m≤21,1≤n≤79)。它们表示氧,氮各自需要的量。 第二行为整数k(1≤k≤1000)表示气缸的个数。 此后的k行,每行包括ai,bi,ci(1≤ai≤21,1≤bi≤79,1≤ci≤800)3ai,bi,ci(1≤ai≤21,1≤bi≤79,1≤ci≤800)3整数。这些各自是:第i个气缸里的氧和氮的容量及汽缸重量。 【输出】 仅一行包含一个整数,为潜水员完成工作所需的气缸的重量总和的最低值。 【输入样例】 5 60 5 3 36 120 10 25 129 5 50 250 1 45 130 4 20 119 【输出样例】 249 二维背包费用问题变形 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 总公司拥有高效设备M台,准备分给下属的N个分公司。各分公司若获得这些设备,可以为国家提供一定的盈利。问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。其中M≤15,N≤10。分配原则:每个公司有权获得任意数目的设备,但总台数不超过设备数M。 【输入】 第一行有两个数,第一个数是分公司数N,第二个数是设备台数M; 接下来是一个N*M的矩阵,表明了第 I个公司分配 J台机器的盈利。 【输出】 第一行输出最大盈利值; 接下N行,每行有2个数,即分公司编号和该分公司获得设备台数。 【输入样例】 3 3 //3个分公司分3台机器 30 40 50 20 30 50 20 25 30 【输出样例】 70 //最大盈利值为70 1 1 //第一分公司分1台 2 1 //第二分公司分1台 3 1 //第三分公司分1台 思路:分组背包模型求具体方案 426. 开心的金明 - AcWing题库 10. 有依赖的背包问题 - AcWing题库 12. 背包问题求具体方案 - AcWing题库 有 N件物品和一个容量是 V的背包。每件物品只能使用一次。 第 i件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。 输出 字典序最小的方案。这里的字典序是指:所选物品的编号所构成的序列。物品的编号范围是1…N。 输入格式 第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。 接下来有 N行,每行两个整数vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。 输出格式 输出一行,包含若干个用空格隔开的整数,表示最优解中所选物品的编号序列,且该编号序列的字典序最小。 物品编号范围是1…N。 数据范围 0 0 输入样例 4 5 1 2 2 4 3 4 4 6 输出样例: 1 4 487. 金明的预算方案 - AcWing题库 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间金明自己专用的很宽敞的房间。 更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过N元钱就行”。 今天一早,金明就开始做预算了,他把想买的物品分为两类:主件与附件,附件是从属于某个主件的,下表就是一些主件与附件的例子: 如果要买归类为附件的物品,必须先买该附件所属的主件。 每个主件可以有0个、1个或2个附件。 附件不再有从属于自己的附件。 金明想买的东西很多,肯定会超过妈妈限定的N元。 于是,他把每件物品规定了一个重要度,分为5等:用整数1~5表示,第5等最重要。 他还从因特网上查到了每件物品的价格(都是10元的整数倍)。 他希望在不超过N元(可以等于N元)的前提下,使每件物品的价格与重要度的乘积的总和最大。 设第j件物品的价格为v[j],重要度为w[j],共选中了k件物品,编号依次为j1,j2,…,jk,则所求的总和为: v[j1]∗w[j1]+v[j2]∗w[j2]+…+v[jk]∗w[jk](其中*为乘号) 请你帮助金明设计一个满足要求的购物单。 输入格式 输入文件的第1行,为两个正整数,用一个空格隔开:N m,其中N表示总钱数,m为希望购买物品的个数。 从第2行到第m+1行,第j行给出了编号为j-1的物品的基本数据,每行有3个非负整数v p q,其中v表示该物品的价格,p表示该物品的重要度(1~5),q表示该物品是主件还是附件。 如果q=0,表示该物品为主件,如果q>0,表示该物品为附件,q是所属主件的编号。 输出格式 输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(<200000)。 数据范围 N<32000,m<60,v<10000 输入样例: 1000 5 800 2 0 400 5 1 300 5 1 400 3 0 500 2 0 输出样例: 2200 思路:分组背包问题。 【题目描述】 这条街上一共有 N 家店铺,每家店中都有一些现金。阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。 作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金? 【输入】 接下来的每组数据,第一行是一个整数N(1≤N≤100,000) ,表示一共有N家店铺。第二行是N个被空格分开的正整数,表示每一家店铺中的现金数量。每家店铺中的现金数量均不超过1000。 【输出】 【输入样例】 对于第二组样例,阿福选择第1和4家店铺行窃,获得的现金数量为10+14=24。 状态机模型 给定一个长度为 N 的数组,数组中的第 i 个数字表示一个给定股票在第 i 天的价格。 设计一个算法来计算你所能获取的最大利润,你最多可以完成 k 笔交易。 注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。一次买入卖出合为一笔交易。 输入格式 第二行包含 N 个不超过 10000 的正整数,表示完整的数组。 输出格式 数据范围 样例2:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。共计利润 4+3 = 7. 题目描述: 农夫约翰有一片 N∗M 的矩形土地。 最近,由于降雨的原因,部分土地被水淹没了。 现在用一个字符矩阵来表示他的土地。 每个单元格内,如果包含雨水,则用”W”表示,如果不含雨水,则用”.”表示。 现在,约翰想知道他的土地中形成了多少片池塘。 每组相连的积水单元格集合可以看作是一片池塘。 每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。 请你输出共有多少片池塘,即矩阵中共有多少片相连的”W”块。 输入格式 第一行包含两个整数 N 和 M。 接下来 N 行,每行包含 M 个字符,字符为”W”或”.”,用以表示矩形土地的积水状况,字符之间没有空格。 输出格式 输出一个整数,表示池塘数目。 数据范围 1≤N,M≤1000 图1是一个城堡的地形图。请你编写一个程序,计算城堡一共有多少房间,最大的房间有多大。城堡被分割成m*n(m≤50,n≤50)个方块,每个方块可以有0~4面墙。 输入 程序从标准输入设备读入数据。第一行是两个整数,分别是南北向、东西向的方块数。在接下来的输入行里,每个方块用一个数字(0≤p≤50)描述。用一个数字表示方块周围的墙,1表示西墙,2表示北墙,4表示东墙,8表示南墙。每个方块用代表其周围墙的数字之和表示。城堡的内墙被计算两次,方块(1,1)的南墙同时也是方块(2,1)的北墙。输入的数据保证城堡至少有两个房间。 输出 城堡的房间数、城堡中最大房间所包括的方块数。结果显示在标准输出设备上。 样例输入 4 7 11 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13 样例输出 5 9 分析: 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 题目描述: FGD小朋友特别喜欢爬山,在爬山的时候他就在研究山峰和山谷。 为了能够对旅程有一个安排,他想知道山峰和山谷的数量。 给定一个地图,为FGD想要旅行的区域,地图被分为 n×n 的网格,每个格子 (i,j) 的高度 w(i,j) 是给定的。 若两个格子有公共顶点,那么它们就是相邻的格子,如与 (i,j) 相邻的格子有(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1) 我们定义一个格子的集合 S 为山峰(山谷)当且仅当: S 的所有格子都有相同的高度。 S 的所有格子都连通。 对于 s 属于 S,与 s 相邻的 s′ 不属于 S,都有 ws>ws′(山峰),或者 ws 如果周围不存在相邻区域,则同时将其视为山峰和山谷。 你的任务是,对于给定的地图,求出山峰和山谷的数量,如果所有格子都有相同的高度,那么整个地图即是山峰,又是山谷。 输入格式 第一行包含一个正整数 n,表示地图的大小。 接下来一个 n×n 的矩阵,表示地图上每个格子的高度 w。 输出格式 共一行,包含两个整数,表示山峰和山谷的数量。 数据范围 1≤n≤1000, 0≤w≤10^9 输入样例: 5 8 8 8 7 7 7 7 8 8 7 7 7 7 7 7 7 8 8 7 8 7 8 8 8 8 输出样例1: 2 1 给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0或 1,其中 0表示可以走的路,1表示不可通过的墙壁。 最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。 请问,该人从左上角移动至右下角 (n,m)处,至少需要移动多少次。 数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。 输入格式 第一行包含两个整数 n和 m。 接下来 n行,每行包含 m个整数(0或 1),表示完整的二维数组迷宫。 输出格式 输出一个整数,表示从左上角移动至右下角的最少移动次数。 数据范围 1≤n,m≤100 输入样例: 5 5 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0 输出样例: 8 bfs:一层一层地向外进行扩展,直到搜到终点位置,本质是队列,最先搜到的位置一定是最短路径,所以bfs有最短路径。 188. 武士风度的牛 - AcWing题库 农民John有很多牛,他想交易其中一头被Don称为The Knight的牛。 这头牛有一个独一无二的超能力,在农场里像Knight一样地跳(就是我们熟悉的象棋中马的走法)。 虽然这头神奇的牛不能跳到树上和石头上,但是它可以在牧场上随意跳,我们把牧场用一个x,y的坐标图来表示。 这头神奇的牛像其它牛一样喜欢吃草,给你一张地图,上面标注了The Knight的开始位置,树、灌木、石头以及其它障碍的位置,除此之外还有一捆草。 现在你的任务是,确定The Knight要想吃到草,至少需要跳多少次。 The Knight的位置用’K’来标记,障碍的位置用’*’来标记,草的位置用’H’来标记。 这里有一个地图的例子: The Knight 可以按照下图中的A,B,C,D…这条路径用5次跳到草的地方(有可能其它路线的长度也是5): 注意: 数据保证一定有解。 输入格式: 第1行: 两个数,表示农场的列数C(C<=150)和行数R(R<=150)。 第2…R+1行: 每行一个由C个字符组成的字符串,共同描绘出牧场地图。 输出格式: 一个整数,表示跳跃的最小次数。 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点N(0≤N≤100000),牛位于点K(0≤K≤100000)。农夫有两种移动方式: 1、从X移动到X−1或X+1,每次移动花费一分钟 2、从X移动到2×X,每次移动花费一分钟 假设牛没有意识到农夫的行动,站在原地不动。农夫最少要花多少时间才能抓住牛? 【输入】 两个整数,N和K。 【输出】 一个整数,农夫抓到牛所要花费的最小分钟数。 【输入样例】 5 17 【输出样例】 4 最短路径的一维扩展 173. 矩阵距离 - AcWing题库 输入格式 第一行两个整数 N,M。 接下来一个 N 行 M 列的 01 矩阵,数字之间没有空格。 输出格式 一个 N 行 M 列的矩阵 B,相邻两个整数之间用一个空格隔开。 数据范围 1≤N,M≤1000 输入样例: 3 4 0001 0011 0110 输出样例: 3 2 1 0 2 1 0 0 1 0 0 1 题意 1107. 魔板 - AcWing题库 Rubik 先生在发明了风靡全球的魔方之后,又发明了它的二维版本——魔板。 这是一张有 8 个大小相同的格子的魔板: 1 2 3 4 8 7 6 5 我们知道魔板的每一个方格都有一种颜色。 这 8 种颜色用前 8 个正整数来表示。 可以用颜色的序列来表示一种魔板状态,规定从魔板的左上角开始,沿顺时针方向依次取出整数,构成一个颜色序列。 对于上图的魔板状态,我们用序列 (1,2,3,4,5,6,7,8) 来表示,这是基本状态。 这里提供三种基本操作,分别用大写字母 A,B,C 来表示(可以通过这些操作改变魔板的状态): A:交换上下两行; B:将最右边的一列插入到最左边; C:魔板中央对的4个数作顺时针旋转。 下面是对基本状态进行操作的示范: A: 8 7 6 5 1 2 3 4 B: 4 1 2 3 5 8 7 6 C: 1 7 2 4 8 6 3 5 对于每种可能的状态,这三种基本操作都可以使用。 你要编程计算用最少的基本操作完成基本状态到特殊状态的转换,输出基本操作序列。 注意:数据保证一定有解。 输入格式 输入仅一行,包括 8 个整数,用空格分开,表示目标状态。 输出格式 输出文件的第一行包括一个整数,表示最短操作序列的长度。 如果操作序列的长度大于0,则在第二行输出字典序最小的操作序列。 数据范围 输入数据中的所有数字均为 1 到 8 之间的整数。 输入样例: 2 6 8 4 5 7 3 1 输出样例: 7 BCABCCB 变成目标状态最少需要多少操作? 把初状态用队列存储,然后进行bfs搜索每个状态,用哈希表存储每个状态 先把每一个状态进行存储,用哈希表。 按照最小字典序顺序去搜索,能够搜到最小字典序的顺序。 175. 电路维修 - AcWing题库 达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。 翰翰的家里有一辆飞行车。 有一天飞行车的电路板突然出现了故障,导致无法启动。 电路板的整体结构是一个 R 行 C 列的网格(R,C≤500),如下图所示。 每个格点都是电线的接点,每个格子都包含一个电子元件。 电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。 在旋转之后,它就可以连接另一条对角线的两个接点。 电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。 达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。 她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。 不过,电路的规模实在是太大了,达达并不擅长编程,希望你能够帮她解决这个问题。 注意:只能走斜向的线段,水平和竖直线段不能走。 输入格式 输入文件包含多组测试数据。 第一行包含一个整数 T,表示测试数据的数目。 对于每组测试数据,第一行包含正整数 R 和 C,表示电路板的行数和列数。 之后 R 行,每行 C 个字符,字符是"/"和"\"中的一个,表示标准件的方向。 输出格式 对于每组测试数据,在单独的一行输出一个正整数,表示所需的最小旋转次数。 如果无论怎样都不能使得电源和发动机之间连通,输出 NO SOLUTION。 数据范围 1≤R,C≤500, 1≤T≤5 输入样例: 1 3 5 \\/\\ \\/// /\\\\ 输出样例: 1 样例解释 样例的输入对应于题目描述中的情况。 只需要按照下面的方式旋转标准件,就可以使得电源和发动机之间连通。 点的偏移量 190. 字串变换 - AcWing题库 已知有两个字串 A, B 及一组字串变换的规则(至多 6 个规则): A1→B1 A2→B2 … 规则的含义为:在 A 中的子串 A1 可以变换为 B1、A2 可以变换为 B2…。 例如:A=abcd B=xyz 变换规则为: abc → xu ud →y y →yz 则此时,A 可以经过一系列的变换变为 B,其变换的过程为: abcd →xud →xy →xyz 共进行了三次变换,使得 A 变换为 B。 输入格式 输入格式如下: A B A1 B1 A2 B2 … … 第一行是两个给定的字符串 A 和 B。 接下来若干行,每行描述一组字串变换的规则。 所有字符串长度的上限为 20。 输出格式 若在 10 步(包含 10 步)以内能将 A 变换为 B ,则输出最少的变换步数;否则输出 NO ANSWER!。 输入样例: abcd xyz abc xu ud y y yz 输出样例: 3 双向bfs每次都要扩展一层。 A*算法可以降低搜索空间。 178. 第K短路 - AcWing题库 给定一张 N个点(编号 1,2…N),M 条边的有向图,求从起点 S 到终点 T 的第 K 短路的长度,路径允许重复经过点或边。 注意: 每条最短路中至少要包含一条边。 输入格式 第一行包含两个整数 N 和 M。 接下来 M行,每行包含三个整数 A,B 和 L,表示点 A 与点 B 之间存在有向边,且边长为 L。 最后一行包含三个整数S,T 和 K,分别表示起点 S,终点 T 和第 K 短路。 输出格式 输出占一行,包含一个整数,表示第 K 短路的长度,如果第 K 短路不存在,则输出 −1。 数据范围 1≤S,T≤N≤1000, 0≤M≤104, 1≤K≤1000, 1≤L≤100 输入样例: 2 2 1 2 5 2 1 4 1 2 2 输出样例: 14 179. 八数码 - AcWing题库 在一个 3×3的网格中,1∼8 这 8 个数字和一个 X 恰好不重不漏地分布在这 3×3 的网格中。 例如: 1 2 3 X 4 6 7 5 8 在游戏过程中,可以把 X 与其上、下、左、右四个方向之一的数字交换(如果存在)。 我们的目的是通过交换,使得网格变为如下排列(称为正确排列): 1 2 3 4 5 6 7 8 X 例如,示例中图形就可以通过让 X 先后与右、下、右三个方向的数字交换成功得到正确排列。 交换过程如下: 1 2 3 1 2 3 1 2 3 1 2 3 X 4 6 4 X 6 4 5 6 4 5 6 7 5 8 7 5 8 7 X 8 7 8 X 把 X 与上下左右方向数字交换的行动记录为 u、d、l、r。 现在,给你一个初始网格,请你通过最少的移动次数,得到正确排列。 输入格式 输入占一行,将 3×3 的初始网格描绘出来。 例如,如果初始网格如下所示: 1 2 3 x 4 6 7 5 8 则输入为:1 2 3 x 4 6 7 5 8 输出格式 输出占一行,包含一个字符串,表示得到正确排列的完整行动记录。 如果答案不唯一,输出任意一种合法方案即可。 如果不存在解决方案,则输出 unsolvable。 输入样例: 2 3 4 1 5 x 7 6 8 输出样例 ullddrurdllurdruldr 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由n×n的格点组成,每个格点只有22种状态,.和#,前者表示可以通行后者表示不能通行。同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,问在不走出迷宫的情况下能不能办到。如果起点或者终点有一个不能通行(为#),则看成无法办到。 【输入】 第1行是测试数据的组数k,后面跟着k组输入。每组测试数据的第1行是一个正整数n(1≤n≤100),表示迷宫的规模是n×n的。接下来是一个n×n的矩阵,矩阵中的元素为.或者#。再接下来一行是4个整数ha,la,hb,lb,描述A处在第ha行, 第la列,B处在第hb行, 第lb列。注意到ha,la,hb,lb全部是从0开始计数的。 【输出】 k行,每行输出对应一个输入。能办到则输出“YES”,否则输出“NO”。 【输入样例】 2 3 .## ..# #.. 0 0 2 2 5 ..... ###.# ..#.. ###.. ...#. 0 0 4 0 【输出样例】 YES NO 思路:简单dfs 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。 【输入】 包括多组数据。每组数据的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下: 1)‘.’:黑色的瓷砖; 2)‘#’:红色的瓷砖; 3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每组数据中唯一出现一次。 当在一行中读入的是两个零时,表示输入结束。 【输出】 对每组数据,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。 【输入样例】 6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 0 0 【输出样例】 45 思路:简单dfs搜索。 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 马在中国象棋以日字形规则移动。 请编写一段程序,给定n×m大小的棋盘,以及马的初始位置(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。 【输入】 第一行为整数T(T < 10),表示测试数据组数。 每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标n,m,x,y。(0≤x≤n-1,0≤y≤m-1, m < 10, n < 10)。 【输出】 每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,0为无法遍历一次。 【输入样例】 1 5 4 0 0 【输出样例】 32 外部搜索的实现。 问题描述 单词接龙是一个与我们经常玩的成语接龙相类似的游戏,现在我们已知一组单词,且给定一个开头的字母,要求出以这个字母开头的最长的“龙”(每个单词都最多在“龙”中出现两次),在两个单词相连时,其重合部分合为一部分,例如 beast和astonish,如果接成一条龙则变为beastonish,另外相邻的两部分不能存在包含关系,例如at 和 atide 间不能相连。 输入格式 输入的第一行为一个单独的整数n (n<=20)表示单词数,以下n 行每行有一个单词,输入的最后一行为一个单个字符,表示“龙”开头的字母。你可以假定以此字母开头的“龙”一定存在. 输出格式 只需输出以此字母开头的最长的“龙”的长度 样例输入 5 at touch cheat choose tact a 样例输出 23 样例说明 连成的“龙”为atoucheatactactouchoose 含有注释 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 给定n个正整数,将它们分组,使得每组中任意两个数互质。至少要分成多少个组? 【输入】 第一行是一个正整数n。1 ≤ n ≤ 10。 第二行是n个不大于10000的正整数。 【输出】 一个正整数,即最少需要的组数。 【输入样例】 6 14 20 33 117 143 175 【输出样例】 3 按照当前组可以放哪些数进行搜索 。 当前数可以放哪些组进行搜索。 165. 小猫爬山 - AcWing题库 翰翰和达达饲养了 N 只小猫,这天,小猫们要去爬山。 经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕>_<)。 翰翰和达达只好花钱让它们坐索道下山。 索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1、C2……CN。 当然,每辆缆车上的小猫的重量之和不能超过 W。 每租用一辆缆车,翰翰和达达就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山? 输入格式 第 1 行:包含两个用空格隔开的整数,N 和 W。 第 2..N+1 行:每行一个整数,其中第 i+1 行的整数表示第 i只小猫的重量Ci。 输出格式 输出一个整数,表示最少需要多少美元,也就是最少需要多少辆缆车。 数据范围 1≤N≤18, 1≤Ci≤W≤1e8 输入样例: 5 1996 1 2 1994 12 29 输出样例: 2 按照当前猫可以放在哪些组进行搜索。 166. 数独 - AcWing题库 167. 木棒 - AcWing题库 168. 生日蛋糕 - AcWing题库 170. 加成序列 - AcWing题库 171. 送礼物 - AcWing题库 180. 排书 - AcWing题库 181. 回转游戏 - AcWing题库 德克萨斯纯朴的民眾们这个夏天正在遭受巨大的热浪!!!他们的德克萨斯长角牛吃起来不错,可是他们并不是很擅长生產富含奶油的乳製品。Farmer John此时以先天下之忧而忧,后天下之乐而乐的精神,身先士卒地承担起向德克萨斯运送大量的营养冰凉的牛奶的重任,以减轻德克萨斯人忍受酷暑的痛苦。 FJ已经研究过可以把牛奶从威斯康星运送到德克萨斯州的路线。这些路线包括起始点和终点先一共经过T (1 <= T <= 2,500)个城镇,方便地标号為1到T。除了起点和终点外的每个城镇由两条双向道路连向至少两个其它的城镇。每条道路有一个通过费用(包括油费,过路费等等)。 给定一个地图,包含C (1 <= C <= 6,200)条直接连接2个城镇的道路。每条道路由道路的起点Rs,终点Re (1 <= Rs <= T; 1 <= Re <= T),和花费(1 <= Ci <= 1,000)组成。求从起始的城镇Ts (1 <= Ts <= T)到终点的城镇Te(1 <= Te <= T)最小的总费用。 第一行: 4个由空格隔开的整数: T, C, Ts, Te; 第2到第C+1行: 第i+1行描述第i条道路。有3个由空格隔开的整数: Rs, Re和Ci。 一个单独的整数表示从Ts到Te的最小总费用。数据保证至少存在一条道路。 【样例说明】 5->6->1->4 (3 + 1 + 3) 思路:朴素版的dijkstra算法。 spfa算法 战争时期,前线有n个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。信使负责在哨所之间传递信息,当然,这是要花费一定时间的(以天为单位)。指挥部设在第一个哨所。当指挥部下达一个命令后,指挥部就派出若干个信使向与指挥部相连的哨所送信。当一个哨所接到信后,这个哨所内的信使们也以同样的方式向其他哨所送信。直至所有n个哨所全部接到命令后,送信才算成功。因为准备充足,每个哨所内都安排了足够的信使(如果一个哨所与其他k个哨所有通信联系的话,这个哨所内至少会配备k个信使)。 现在总指挥请你编一个程序,计算出完成整个送信过程最短需要多少时间。 第1行有两个整数n和m,中间用1个空格隔开,分别表示有n个哨所和m条通信线路,且1≤n≤100。 第2至m+1行:每行三个整数i、j、k,中间用1个空格隔开,表示第i个和第j个哨所之间存在通信线路,且这条线路要花费k天。 一个整数,表示完成整个送信过程的最短时间。如果不是所有的哨所都能收到信,就输出-1。 思路:对于每一个点来说,最早接到信的时间,等于他到指挥部的最短距离。 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 思路 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 思路 237. 程序自动分析 - AcWing题库 239. 奇偶游戏 - AcWing题库 有x类,就模x,把他们分成x类 别人更加详细的思路 238. 银河英雄传说 - AcWing题库 有关请参考树状数组 241. 楼兰图腾 - AcWing题库 242. 一个简单的整数问题 - AcWing题库 树状数组和差分的应用,树状数组里面只需要存a数组的差分即可。 243. 一个简单的整数问题2 - AcWing题库 则化简为(b1+b2+...+bx)(x+1)-(b1+2b2+...xbx),只需要同时存储bi和i*bi的前缀和即可。 244. 谜一样的牛 - AcWing题库 求前缀和 (1)单点修改 O(logn) 只递归修改包含当前点的区间。 (2)区间查询 O(logn) 查询也是一个递归的过程,递归到包含当前区间的点中。 1264. 动态求连续区间和 - AcWing题库 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 原题来自:JSOI 2008 给定一个正整数数列 a1,a2,a3,⋯,an ,每一个数都在 0∼p–1之间。可以对这列数进行两种操作: 添加操作:向序列后添加一个数,序列长度变成 n+1; 询问操作:询问这个序列中最后 L个数中最大的数是多少。 程序运行的最开始,整数序列为空。写一个程序,读入操作的序列,并输出询问操作的答案。 【输入】 第一行有两个正整数 m,p,意义如题目描述; 接下来 m 行,每一行表示一个操作。如果该行的内容是 Q L,则表示这个操作是询问序列中最后 L 个数的最大数是多少;如果是 A t,则表示向序列后面加一个数,加入的数是 (t+a)modp。其中,t 是输入的参数,a 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 a=0)。 第一个操作一定是添加操作。对于询问操作,L>0 且不超过当前序列的长度。 【输出】 对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 L个数的最大数。 【输入样例】 10 100 A 97 Q 1 Q 1 A 17 Q 2 A 63 Q 1 Q 1 Q 3 A 99 【输出样例】 97 97 97 60 60 97 245. 你能回答这些问题吗 - AcWing题库 246. 区间最大公约数 - AcWing题库 最大异或和 - 洛谷 题目描述 有 m 个操作,有以下两种操作类型: A x:添加操作,表示在序列末尾添加一个数 xx,序列的长度 n+1。 输出格式 输入输出样例 就是存下来trie的每个版本。 253. 普通平衡树 - AcWing题库 90. 64位整数乘法 - AcWing题库 95. 费解的开关 - AcWing题库 你玩过“拉灯”游戏吗? 25盏灯排成一个 5×5 的方形。 每一个灯都有一个开关,游戏者可以改变它的状态。 每一步,游戏者可以改变某一个灯的状态。 游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。 我们用数字 1 表示一盏开着的灯,用数字 0 表示关着的灯。 下面这种状态 10111 01101 10111 10000 11011 在改变了最左上角的灯的状态后将变成: 01111 11101 10111 10000 11011 再改变它正中间的灯后状态将变成: 01111 11001 11001 10100 11011 给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6 步以内使所有的灯都变亮。 输入格式 第一行输入正整数 n,代表数据中共有 n 个待解决的游戏初始状态。 以下若干行数据分为 n 组,每组数据有 5 行,每行 5 个字符。 每组数据描述了一个游戏的初始状态。 各组数据间用一个空行分隔。 输出格式 一共输出 n 行数据,每行有一个小于等于 6 的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。 对于某一个游戏初始状态,若 66 步以内无法使所有灯变亮,则输出 −1。 数据范围 0 输入样例: 3 00111 01011 10001 11010 11100 11101 11101 11110 11111 11111 01111 11111 11111 11111 11111 输出样例: 3 2 -1 97. 约数之和 - AcWing题库 更加详细方法二: 98. 分形之城 - AcWing题库 99. 激光炸弹 - AcWing题库 思路:二维前缀和的构造。 100. 增减序列 - AcWing题库 102. 最佳牛围栏 - AcWing题库 113. 特殊排序 - AcWing题库 通过sort排序的特殊方式进行排序。 105. 七夕祭 - AcWing题库 106. 动态中位数 - AcWing题库 107. 超快速排序 - AcWing题库 最小交换次数就是逆序对数。 信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn) 【题目描述】 原题来自:Vijos P1512 从前有个人名叫 W and N and B,他有着天才般的记忆力,他珍藏了许多许多的宝藏。在他离世之后留给后人一个难题(专门考验记忆力的啊!),如果谁能轻松回答出这个问题,便可以继承他的宝藏。 题目是这样的:给你一大串数字(编号为 1到 N,大小可不一定哦!),在你看过一遍之后,它便消失在你面前,随后问题就出现了,给你 M个询问,每次询问就给你两个数字 A,B,要求你瞬间就说出属于 A 到 B这段区间内的最大数。 一天,一位美丽的姐姐从天上飞过,看到这个问题,感到很有意思(主要是据说那个宝藏里面藏着一种美容水,喝了可以让这美丽的姐姐更加迷人),于是她就竭尽全力想解决这个问题。BUT,她每次都以失败告终,因为这数字的个数是在太多了!于是她请天才的你帮他解决。如果你帮她解决了这个问题,可是会得到很多甜头的哦! 【输入】 第一行一个整数 N表示数字的个数,接下来一行为 N个数。第三行读入一个 M,表示你看完那串数后需要被提问的次数,接下来 M行,每行都有两个整数 A,B。 【输出】 输出共 M行,每行输出一个数,表示对一个问题的回答。 【输入样例】 6 34 1 8 123 3 2 4 1 2 1 5 3 4 2 3 【输出样例】 34 123 123 8 注意:RMQ算法只能求静态数组区间的最大值,不能求动态数组区间最大值。#include1.2.2登山
#include1.2.3合唱队形
#include1.2.4好友城市
#include1.2.5最大上升子序列和
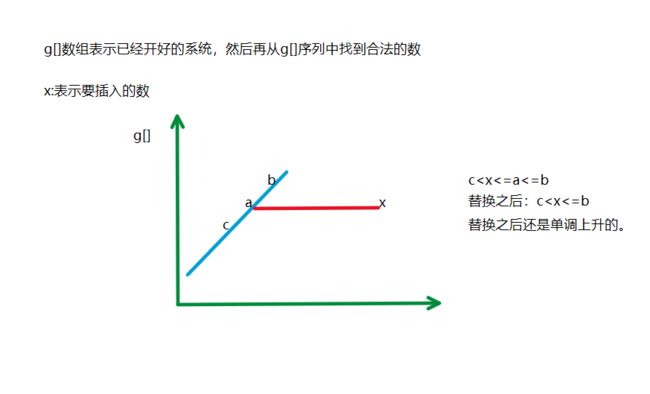
#include1.2.6拦截导弹
#include1.2.7导弹防御系统
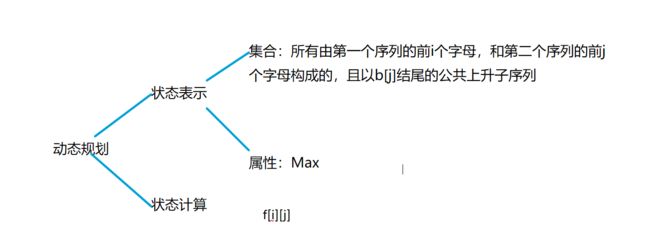
#include1.2.8最长上升公共子序列
#include#include#include1.3 背包模型
1.3.1采药
#include1.3.2装箱问题
#include1.3.3宠物小精灵之收服
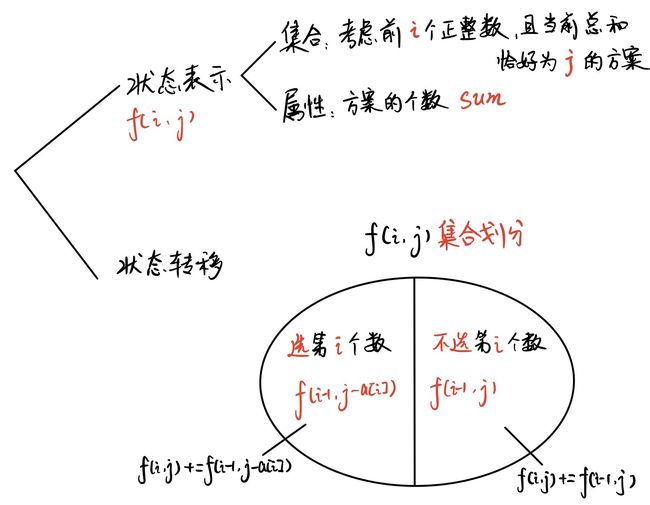
#include1.3.4数字组合
#include#include 1.3.5买书
#include#include1.3.6货币系统
#include1.3.7货币系统
#include1.3.8多重背包问题III
1.3.9庆功会
#include#include1.3.10混合背包问题
1.3.11二维费用的背包问题
1.3.12潜水员
#include1.3.13机器分配
#include1.3.14开心的金明
#include 1.3.15有依赖的背包问题
1.3.16背包问题求方案数
1.3.17背包问题求具体方案
#include1.3.18能量石
1.3.19金明的预算方案
#include 1.4 状态机模型
1.4.1大盗阿福
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
输入的第一行是一个整数T(T≤50) ,表示一共有T组数据。
对于每组数据,输出一行。该行包含一个整数,表示阿福在不惊动警察的情况下可以得到的现金数量。
2
3
1 8 2
4
10 7 6 14
【输出样例】
8
24
【提示】
对于第一组样例,阿福选择第2家店铺行窃,获得的现金数量为8。
————————————————
信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn)#include//状态机模型
#include1.4.2股票买卖IV
第一行包含整数 N 和 k,表示数组的长度以及你可以完成的最大交易数量。
输出一个整数,表示最大利润。
1≤N≤10^5,
1≤k≤100
输入样例1:
3 2
2 4 1
输出样例1:
2
输入样例2:
6 2
3 2 6 5 0 3
输出样例2:
7
样例解释
样例1:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
————————————————
1057. 股票买卖 IV - AcWing题库#include 1.4.3股票买卖V
1.4.4设计密码
1.4.5修复DNA
1.5 状态压缩DP
1.5.1小国王
1.5.2玉米田
1.5.3炮兵阵地
1.5.4愤怒的小鸟
1.5.5宝藏
1.6 区间DP
1.6.1环形石子合并
1.6.2能量项链
1.6.3加分二叉树
1.6.4凸多边形的划分
1.6.5棋盘分割
1.7 树形DP
1.7.1树的最长路径
1.7.2树的中心
1.7.3数字转换
1.7.4二叉苹果树
1.7.5战略游戏
1.7.6皇宫看守
1.8 数位DP
1.8.1度的数量
1.8.2数字游戏
1.8.3Windy数
1.8.4数字游戏II
1.8.5不要62
1.8.6恨7不成妻
1.9 单调队列优化的DP问题
1.9.1最大子序和
1.9.2修剪草坪
1.9.3旅行问题
1.9.4烽火传递
1.9.5绿色通道
1.9.6理想的正方形
1.10 斜率优化的DP问题
1.10.1任务安排1
1.10.2任务安排2
1.10.3任务安排3
1.10.4运输小猫
2.搜索
BFS
2.1 Flood Fill
2.1.1池塘计数
#include2.1.2城堡问题
#include 2.1.3山谷和山峰
#include2.2 最短路模型
2.2.1迷宫问题
#include2.2.2武士风度的牛
![]()
#include2.2.3抓住那头牛
#include2.3 多源BFS
2.3.1矩阵距离
#include2.4 最小步数模型
2.4.1魔板
#include 2.5 双端队列广搜
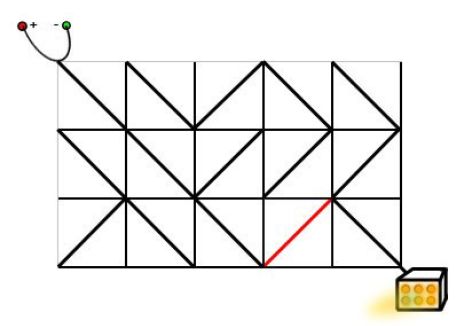
2.5.6电路维修
#include 2.6 双向广搜
2.6.1字串变换
#include 2.7 A*
2.7.1第K短路
/*
A* 应用场景:
起点→终点的最短距离
状态空间 >> 1e10
启发函数减小搜索空间
A*算法:
while(q.size())
t ← 优先队列的队头 小根堆
当终点第一次出队时 break;
从起点到当前点的真实距离 d_real
从当前点到终点的估计距离 d_estimate
选择一个估计距离最小的点 min(d_estimate)
for j in ne[t]:
将邻边入队
A*算法条件:
估计距离<=真实距离
d[state] + f[state] = 起点到state的真实距离 + state到终点的估计距离=估计距离
^
d[state] + g[state] = 起点到state的真实距离 + state到终点的真实距离=真实距离
一定是有解才有 d[i] >= d[最优] = d[u]+f[u]
f[u] >= 0
证明终点第一次出队列即最优解
1 假设终点第一次出队列时不是最优
则说明当前队列中存在点u
有 d[估计]< d[真实]
d[u] + f[u] <= d[u] + g[u] = d[队头终点]
即队列中存在比d[终点]小的值,
2 但我们维护的是一个小根堆,没有比d[队头终点]小的d[u],矛盾
证毕
A* 不用判重
以边权都为1为例
A o→o→o
↑ ↓
S o→o→o→o→o→o→o T
B
dist[A] = dist[S]+1 + f[A] = 7
dist[B] = dist[S]+1 + f[B] = 5
则会优先从B这条路走到T
B走到T后再从A这条路走到T
*/
/*
本题
建反向边dijkstra求各点到终点的距离作为估计值f[u]
*/
#include 2.7.2八数码
#include DFS
2.8DFS 之连通性模型
2.8.1迷宫
#include2.8.2红与黑
#include2.9DFS 之搜索顺序
2.9.1马走日
#include2.9.2单词接龙
#include#include2.9.3分成互质组
#include#include2.10DFS之剪枝与优化
2.10.1小猫爬山
#include2.10.2数独
#include2.10.3木棒
2.10.4生日蛋糕
2.11 迭代加深
2.11.1加成序列
2.12 双向DFS
2.12.1送礼物
2.13 IDA*
2.13.1排书
2.13.2回转游戏
3.图论
3.1单源最短路的建图方式
3.1.1热浪
【题目描述】
【输入】
【输出】
【输入样例】
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
【输出样例】
7
【提示】
#include#include3.1.2信使
【题目描述】
【输入】
【输出】
【输入样例】
4 4
1 2 4
2 3 7
2 4 1
3 4 6
【输出样例】
11
3.2 单源最短路的综合应用
3.3 单源最短路的扩展应用
3.4 floyd算法及其变形
3.5 最小生成树的典型应用
3.6 最小生成树的扩展应用
3.7 SPFA求负环
3.8 差分约束
3.9 最近公共祖先
3.10 有向图的强连通分量
3.11 无向图的双连通分量
3.12 二分图
3.13 欧拉回路和欧拉路径
3.14 拓扑排序
4.高级数据结构
4.1 并查集
4.1.1格子游戏
#include4.1.2搭配购买
#include4.1.3程序自动分析
#include4.1.4奇偶游戏
#include #include 4.1.5银河英雄传说
#include4.2 树状数组
4.2.1楼兰图腾
4.2.2一个简单的整数问题
#include4.2.3一个简单的整数问题2
#include4.2.4谜一样的牛
4.3线段树
4.3.0动态区间求连续和
#include4.3.1最大数
#include 4.3.2你能回答这些问题吗
#include 4.3.3区间最大公约数
#include 4.3.4一个简单的整数问题2
4.3.5亚特兰蒂斯
4.3.6维护序列
4.4 可持久化数据结构
4.4.1最大异或和
给定一个非负整数序列 {a},初始长度为n。
Q l r x:询问操作,你需要找到一个位置 p,满足l≤p≤r,使得:a[p]⊕a[p+1]⊕...⊕a[N]⊕x 最大,输出最大是多少。
输入格式
第一行包含两个整数 N,M,含义如问题描述所示。
第二行包含 N个非负整数,表示初始的序列A 。
接下来 M行,每行描述一个操作,格式如题面所述。
假设询问操作有 T 个,则输出应该有 T 行,每行一个整数表示询问的答案。
输入 #1复制
5 5
2 6 4 3 6
A 1
Q 3 5 4
A 4
Q 5 7 0
Q 3 6 6
输出 #1复制
4
5
6
思路:4.4.2第K小数
4.5 平衡树——Treap
4.5.1普通平衡树
#include4.5.2营业额统计
4.6 AC自动机
4.6.1搜索关键词
4.6.2单词
5.数学知识
5.1 筛质数
5.2 分解质因数
5.3 快速幂
5.4 约数个数
5.5 欧拉函数
5.6 同余
5.7 矩阵乘法
5.8 组合计数
5.9 高斯消元
5.10 容斥原理
5.11 概率与数学期望
5.12 博弈论
6.基础算法
6.1 位运算
6.1.1 64位整数乘法
#include6.2 递归
6.2.1费解的开关
#include6.2.2约数之和
#include 6.2.3分形之城
6.3 前缀和与差分
6.3.1激光炸弹
#include6.3.2增减序列
#include6.4 二分
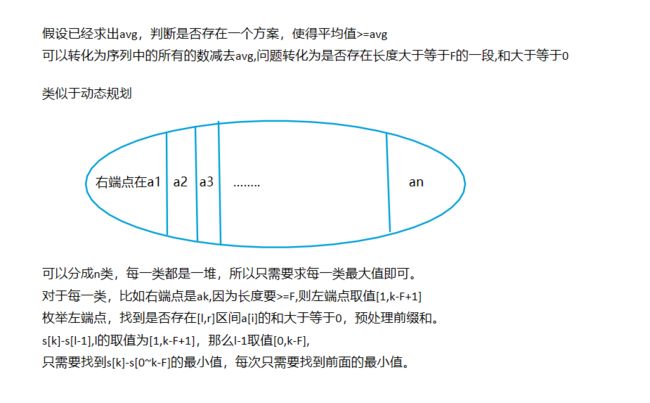
6.4.1最佳牛围栏
#include 6.4.2特殊排序
// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.
class Solution {
public:
vector6.5 排序
6.5.1七夕祭
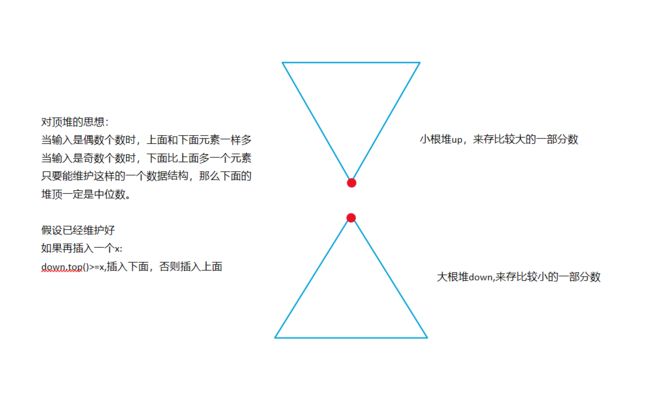
6.5.2动态中位数
#include 6.5.3超快速排序
#include 6.6 RMQ
6.6.1天才的记忆
#include