剑指 Offer(第 2 版)力扣 (LeetCode) Java刷题记录
记录刷题过程
目录
- 03 数组中重复的数字
- 04 二维数组中的查找
- 05 替换空格
- 06 从尾到头打印链表
- 07 重建二叉树
- 09 用2个栈实现队列
- 10-1 斐波拉契数列
- 10-2 青蛙跳台阶问题
- 11 旋转数组的最下数字
- 12 矩阵中的路径
- 13 机器人的运动范围
- 14-1 剪绳子
- 14-2 剪绳子2
- 15 二进制中1的个数
- 16 数值的整数次方
- 17 打印从1到最大的n位数
- 18 删除链表的节点
- 19 正则表达式匹配
- 20 表示数值的字符串
- 21 调整数组顺序使奇数位于偶数前面
- 22 链表中倒数第k个节点
- 24 反转链表
- 25 合并两个排序的链表
- 26 树的子结构
- 27 二叉树的镜像
- 28 对称的二叉树
- 29 顺时针打印矩阵
- 30 包含min函数的栈
- 31 栈的压入、弹出序列
- 32 - I 从上到下打印二叉树
- 32 - II 从上到下打印二叉树 II
- 32 - III 从上到下打印二叉树 III
- 33 二叉搜索树的后序遍历序列
- 34 二叉树中和为某一值的路径
- 35 复杂链表的复制
- 36 二叉搜索树与双向链表
- 37 序列化二叉树
- 38 字符串的排列
- 39 数组中出现次数超过一半的数字
- 40 最小的k个数
- 41 数据流中的中位数
- 42 连续子数组的最大和
- 43 1~n整数中1出现的次数
- 44 数字序列中某一位的数字
- 45 把数组排成最小的数
- 46 把数字翻译成字符串
- 47 礼物的最大价值
- 48 最长不含重复字符的子字符串
- 49 丑数
- 50 第一个只出现一次的字符
- 51 数组中的逆序对
- 52 两个链表的第一个公共节点
- 53- I 在排序数组中查找数字
- 53-II 0~n-1中缺失的数字
- 54 二叉搜索树的第k大节点
- 55-I 二叉树的深度
- 55-II 平衡二叉树
- 56-I 数组中数字出现的次数
- 56-II 数组中数字出现的次数 II
- 57 和为s的两个数字
- 57-II 和为s的连续正整数序列
- 58-I 翻转单词顺序
- 58-II 左旋转字符串
- 59-I 滑动窗口的最大值
- 59-II 队列的最大值
- 60 n个骰子的点数
- 61 扑克牌中的顺子
- 62 圆圈中最后剩下的数字
- 63 股票的最大利润
- 64 求1+2+...+n
- 65 不用加减乘除做加法
- 66 构建乘积数组
- 67 把字符串转化成整数
- 68 - I 二叉搜索树的最近公共祖先
- 68 - II 二叉搜索树的最近公共祖先
03 数组中重复的数字
class Solution {
// public int findRepeatNumber(int[] nums) {
// // 使用 map 数组来记录数字出现的次数,效果类似 HashSet ,但是性能更好
// int[] map = new int[nums.length];
// for (int num : nums) {
// map[num]++;
// if (map[num] == 2) return num;
// }
// return -1;
// }
// 原地排序法,上面的方法更好理解
public int findRepeatNumber(int[] nums) {
int i = 0;
while (i < nums.length) {
// 如果 nums[i] == i,则向后移动
if (nums[i] == i) {
i++;
continue;
}
if (nums[i] == nums[nums[i]]) return nums[i];
// 交换位置
int tmp = nums[i];
nums[i] = nums[tmp];
nums[tmp] = tmp;
}
return -1;
}
}
04 二维数组中的查找
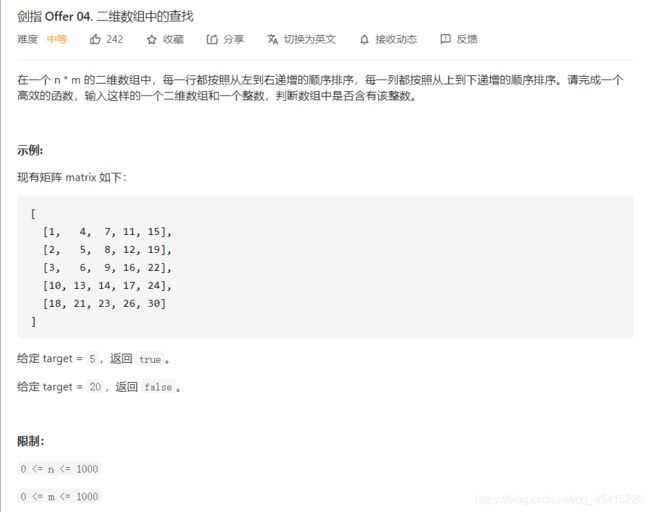
分析:时间复杂度O(M+N)
以左下角的数为例,小于它的数一定在上面,大于它的数一定在右边。因此,可以从左下角(右上角同理)的数开始,与给定的target进行比较,不断移动位置,从而缩小矩阵范围。
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
// 理论上性能比暴力遍历法更好
if (matrix == null || matrix.length == 0) return false;
int row = matrix.length - 1;
int col = 0;
while (row >= 0 && col < matrix[0].length) {
if (matrix[row][col] == target) return true;
else if (target < matrix[row][col]) row--;
else col++;
}
return false;
}
}
05 替换空格

分析:这里我们使用StringBuilder来放置替换空格后的字符串,首先遍历原给定的字符串,然后根据题意填充StringBuilder,最后使用stringBuilder.toString()转化为String输出
class Solution {
public String replaceSpace(String s) {
// 直接遍历,用 StringBuilder 拼接即可
if (s == null || s.length() == 0) return s;
StringBuilder builder = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == ' ') builder.append("%20");
else builder.append(s.charAt(i));
}
return builder.toString();
}
}
06 从尾到头打印链表

分析:此题可以使用递归或者栈,但是下面的方法,最易理解(如果不能理解java里面的链表,可以先百度,在java里面,类就是数据结构)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {
if (head == null) return new int[0];
int length = 0;
ListNode node = head;
// 计算出链表的长度
while (node != null) {
length++;
node = node.next;
}
int[] res = new int[length];
// 正向遍历链表,反向赋值即可
for (int i = length - 1; i >= 0; i--) {
res[i] = head.val;
head = head.next;
}
return res;
}
}
07 重建二叉树
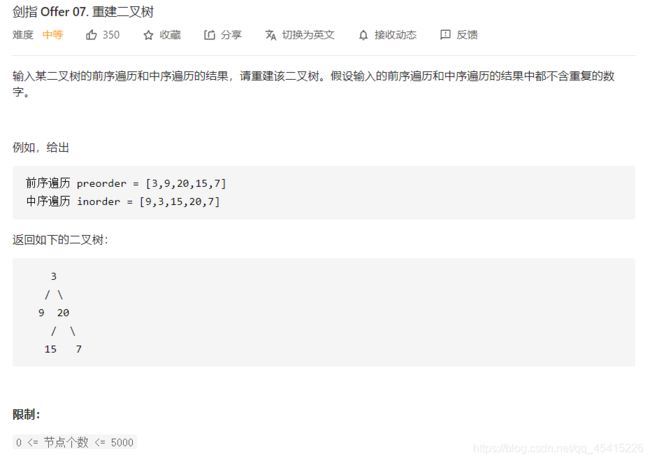
分析:首先我们要知道对于二叉树:3种遍历方式
前序遍历:1.访问根节点 2.前序遍历左子树 3.前序遍历右子树
中序遍历:1.中序遍历左子树 2.访问根节点 3.中序遍历右子树
后序遍历: 1.后序遍历左子树 2.后序遍历右子树 3.访问根节点
这道题通过前序遍历可以知道根节点,接着用该根节点把中序遍历的结果分成左右2个部分,左边部分为左子树中序遍历结果,右边部分为右子树中序遍历结果
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder == null || inorder == null) return new TreeNode();
// 存储中序遍历数组的值和对应索引
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return helper(preorder, 0, preorder.length - 1, 0);
}
public TreeNode helper(int[] preorder, int preL, int preR, int inL) {
// 该树节点遍历完已经
if (preL > preR) return null;
TreeNode root = new TreeNode();
// 根节点
root.val = preorder[preL];
// 根据中序遍历中左子树的长度可以将前序遍历中分为根节点|左子树|右子树3部分
int leftSize = map.get(root.val) - inL;
// 左子树递归
root.left = helper(preorder, preL + 1, preL + leftSize, inL);
// 右子树递归
root.right = helper(preorder, preL + leftSize + 1, preR, inL + leftSize + 1);
return root;
}
}
09 用2个栈实现队列

分析:做这个题的时候,题目看了很久没看懂…

这道题需要用到2个栈,压入数据进入的栈stackA和弹出数据的栈stackB
我们都知道:栈是先进后出,但是队列为先进先出
删除数据时,检查stackB是否还有数据
如果有则直接弹出即可
如果没有,检查stackA是否有数据,如果没有,返回-1;如果有,则把stackA里面的数据全部压入stackB
class CQueue {
// stackA用于push进队首的数
Stack<Integer> stackA;
// stackB用于弹出队尾的数
Stack<Integer> stackB;
public CQueue() {
stackA = new Stack<>();
stackB = new Stack<>();
}
public void appendTail(int value) {
stackA.push(value);
}
public int deleteHead() {
// 出栈stackB不为空,直接弹出
if (!stackB.isEmpty()) return stackB.pop();
else {
// 检查stackA是否为空
if (stackA.isEmpty()) return -1;
else {
// 把stackA里面的元素全部放入stackB
while (!stackA.isEmpty()) {
stackB.push(stackA.pop());
}
}
}
return stackB.pop();
}
}
/**
* Your CQueue object will be instantiated and called as such:
* CQueue obj = new CQueue();
* obj.appendTail(value);
* int param_2 = obj.deleteHead();
*/
10-1 斐波拉契数列
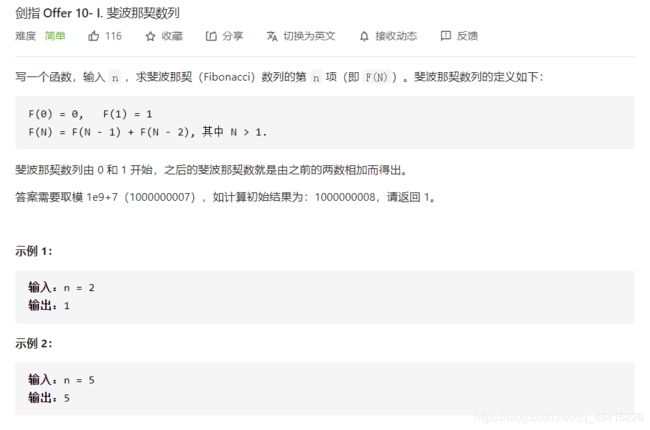
分析:如果单纯采用递归方法,会重复计算一些问题,因此需要利用新的数组来进行缓存
方法1:递归
//利用缓存递归,防止2次计算
class Solution {
private int[] array;
public int fib(int n) {
array = new int[n + 1];
return newFib(n);
}
public int newFib(int n){
if(n < 2) return n;
if(array[n] == 0) array[n] = newFib(n - 1) + newFib(n - 2);
return array[n] % 1000000007;
}
}
方法2:动态规划
//动态规划
class Solution {
public int fib(int n) {
if (n <= 1)
return n;
int[] fib = new int[n + 1];
fib[1] = 1;
for (int i = 2; i <= n; i++)
fib[i] = (fib[i - 1] + fib[i - 2]) % 1000000007;
return fib[n];
}
}
方法3:在方法2的基础上,使用变量替代数组,降低空间复杂度
class Solution {
public int fib(int n) {
// 使用动态规划,同时为了降低空间复杂度,使用3个变量分别保存
// n - 2, n - 1, n 位置的数
// 即下面定义的 preTwo, preOne, res
if (n < 2) return n;
// 前 1 个数
int preOne = 1;
// 前 2 个数
int preTwo = 0;
int res = 0;
for (int i = 2; i <= n; i++) {
res = (preOne + preTwo) % 1000000007;
// 重新赋值
preTwo = preOne;
preOne = res;
}
return res;
}
}
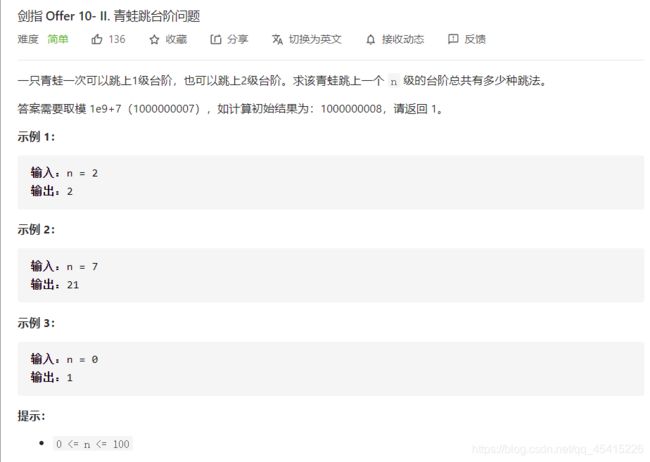
10-2 青蛙跳台阶问题
- 只差1步到第n阶台阶
- 只差2步到第n阶台阶
即f(n) = f(n - 1) + f(n - 2),此时问题就转化为了斐波拉契数列问题
class Solution {
public int numWays(int n) {
// 把跳台阶问题抽象化为一个斐波拉契问题即可,注意 n = 0 ,默认有1种跳法:就是不用跳
if (n < 2) return 1;
int preOne = 1;
int preTwo = 1;
int res = 0;
for (int i = 2; i <= n; i++) {
res = (preOne + preTwo) % 1000000007;
preTwo = preOne;
preOne = res;
}
return res;
}
}
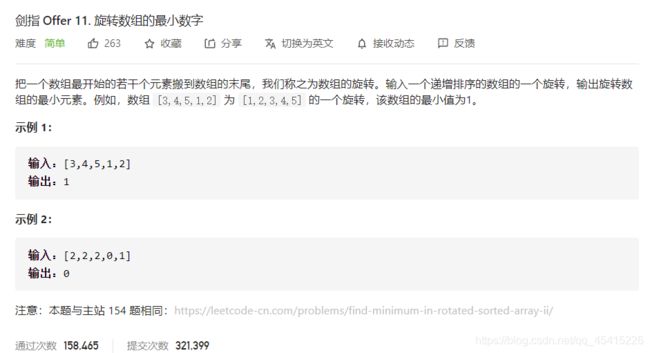
11 旋转数组的最下数字
- mid > high:最小值一定在 (mid+1)—— high 这个范围里面
- mid < high:最小值一定在 low —— mid 这个范围里面
- mid = high: 最小值无法确定,此时应该使high左移,重新二分查找
class Solution {
public int minArray(int[] numbers) {
// 查找一般使用二分法
int left = 0;
int right = numbers.length - 1;
while (left <= right) {
int mid = (left + right) / 2;
// 如果 mid > right,说明旋转点在右侧
if (numbers[mid] > numbers[right]) left = ++mid;
// 如果 mid < right,说明旋转点在左侧,注意此时 mid 可能就是旋转点
else if (numbers[mid] < numbers[right]) right = mid;
// 如果 mid == right,则 right--,以此来缩小查找的范围
// 实际上,当出现 mid == right 时,一定有旋转点左侧的所有元素相等或旋转点右侧的所有元素相等(或两者皆满足)
// 对于寻找此类数组的最小值问题,可直接放弃二分查找,而使用线性查找替代
else right--;
}
return numbers[left];
}
}
12 矩阵中的路径

分析:
采用DFS+回溯法
从矩阵的某一个位置开始,向4个方向移动,如果最后路径无法满足要求,则将设置过的状态进行清除。
class Solution {
public boolean exist(char[][] board, String word) {
int rowL = board.length;
int colL = board[0].length;
for (int i = 0; i < rowL; i++) {
for (int j = 0; j < colL; j++) {
// 找到二维数组中 word 首字母的位置
if (board[i][j] == word.charAt(0)) {
if (dfs(board, i, j, 0, word)) return true;
}
}
}
return false;
}
public boolean dfs(char[][] board, int r, int c, int index, String word) {
// 判断移动位置是否合法
if (r < 0 || r >= board.length || c < 0 || c >= board[0].length || board[r][c] != word.charAt(index)) return false;
// word遍历完成
if (index == word.length() - 1) return true;
// 清空该位置的字母,防止二次搜索
board[r][c] = ' ';
// 向上-下-左-右移动
boolean res = dfs(board, r - 1, c, index + 1, word) || dfs(board, r + 1, c, index + 1, word) ||
dfs(board, r, c - 1, index + 1, word) || dfs(board, r, c + 1, index + 1, word);
// 回溯:将之前清空的字母复原
board[r][c] = word.charAt(index);
return res;
}
}
13 机器人的运动范围

分析:
采用DFS
用深度优先搜索算法,让机器人从[0, 0]开始往下和右移动,直到无法移动为止。
class Solution {
public int movingCount(int m, int n, int k) {
// 标志是否访问过
boolean[][] visited = new boolean[m][n];
return dfs(m, n, k, 0, 0, visited);
}
public int dfs(int m, int n, int k, int r, int c, boolean[][] visited) {
// dfs只能下面
if (r == m || c == n || isGreater(r, c, k) || visited[r][c]) return 0;
// 标记已经走过的位置
visited[r][c] = true;
// 只能向下和向右移动,知道无法移动为止
return 1 + dfs(m, n, k, r + 1, c, visited) + dfs(m, n, k, r, c + 1, visited);
}
// 计算数位和是否大于 k
public boolean isGreater(int r, int c, int k) {
int sum = 0;
while (r != 0) {
// % 可以得到个位数
sum += (r % 10);
// 除号 / 可以去掉个位数
r /= 10;
}
while (c != 0) {
sum += (c % 10);
c /= 10;
}
return sum > k ? true : false;
}
}
14-1 剪绳子

分析:
注意题意:n > 1 同时 m > 1,所以一段绳子,至少分成2段,因此当n=2,n=3时,最大乘积分别为1和2
方法1:贪心算法:越多长度为3的绳子越好
- n % 3 == 0:分成的每1段长度都为3
- n % 3 == 1:取1个3出来和1组成长度为4的绳子,其余全部分成3
- n % 3 == 2:把2分成单独的1段,其余全部分成3
//贪心算法(执行用时更少)
class Solution {
public int cuttingRope(int n) {
// 贪心算法:尽可能多的分成长度为3的段
if (n <= 3) return n - 1;
int a = n / 3;
int b = n % 3;
if (b == 0) return (int)Math.pow(3, a);
else if (b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
方法2:动态规划,用数组来保存每个长度的最大乘积值
class Solution {
public int cuttingRope(int n) {
// 初始化,默认每个值为0
int [] array = new int[n + 1];
array[1] = 1;
array[2] = 1;
for(int i=3; i<=n; i++){
// 把长度为i的绳子,分为2段,1段长为i - j,另一段长为j
for(int j=1; j<i; j++){
// 更新数组里面所存放的array[i]的最大值
// 长度为i - j的一段,有2种情况:继续分或者不分
// array[i - j] * j 第一种:继续分后所得的乘积值
// (i - j) * j 第二种:不分
array[i] = Math.max(array[i], Math.max(array[i - j] * j, (i - j) * j));
}
}
return array[n];
}
}
14-2 剪绳子2
![]()
分析:此题不宜用动态规划,最好是采用贪心算法,且该题2<=n<=1000,会涉及到溢出问题,因此在定义变量的时候,应该用long而不是int。答案需要对结果取模,应该理解为在每一次计算后,都进行取模操作。
class Solution {
public int cuttingRope(int n) {
if (n <= 3) return n - 1;
// 切成3的段数
int a = n / 3;
// 余数
int b = n % 3;
if (b == 0) return (int)getNum(a);
else if (b == 1) return (int)(getNum(a - 1) * 4 % 1000000007);
return (int)(getNum(a) * 2 % 1000000007);
}
public long getNum(int a) {
long res = 1;
while (a-- > 0) {
res *= 3;
res %= 1000000007;
}
return res;
}
}
15 二进制中1的个数

分析:通过n&(n - 1)之间的按位与运算来依次消除二进制串n中尾部的1
按位与运算:
1&1=1
1&0=0
0&1=0
0&0=0
例如:n = 1011(此时n为二进制数,省去了前面的0000…)
n - 1 = (十进制)n - 1 = 10 = (二进制)1010
则n&(n - 1)运算过程为:
n 1011
n - 1 1010
------------------
n&(n - 1) 1010
此时n&(n - 1)的结果1010就消除了n尾部的1,通过这种方式,可以找出n中所有的1
方法1:按位与
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int count = 0;
while(n != 0){
count++;
n &= (n - 1);
}
return count;
}
}
方法2:使用内置函数
Integer.bitCount(n):计算int,long类型的数值在二进制下1的个数(是不是很方便)
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
return Integer.bitCount(n);
}
}
方法3:无符号右移>>>
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int count = 0;
while (n != 0) {
// n & 1 == 1 说明 n 的最后一位为1
count += n & 1;
// 将 n 无符号右移一位,便于下次 & 操作直接比较最后1位
n >>>= 1;
}
return count;
}
}
16 数值的整数次方

分析:采用递归降低时间复杂度
n为奇数和偶数分别对应2种情况
- x n =( x 2 ) n/2
- x n =x * (x 2 ) (n-1)/2
因为 当n为奇数时,(n - 1) / 2 的结果跟 n / 2的结果相同,因此在代码中直接使用n / 2。
class Solution {
// 有个测试用例很有意思:
// 1.000 -2147483648
// 这个输入的 n 值为 int 类型的左边界即最小值
// 当执行 n *= -1时,n 并不会变为正数 2147483648,因为它超出了 int 类型的右边界即最大值2147483647
// 所以,此时得到的 n 仍然为 -2147483648
public double myPow(double x, int n) {
// 标志是否为负数
boolean isNegative = false;
if (n < 0) {
n *= -1;
isNegative = true;
}
// 递归调用方法
double res = helper(x, n);
return isNegative ? 1 / res : res;
}
public double helper(double x, int n) {
if (n == 0) return 1.0;
if (n == 1) return x;
double d = helper(x * x, n / 2);
// 如果 n 为奇数,需要额外乘以 x
if (n % 2 != 0) d *= x;
return d;
}
}
17 打印从1到最大的n位数
class Solution {
public int[] printNumbers(int n) {
int max = (int)Math.pow(10, n) - 1;
int[] res = new int[max];
for (int i = 0; i < max; i++) {
res[i] = i + 1;
}
return res;
}
}
18 删除链表的节点

分析:把待删除节点的next赋给待删除节点上一个节点的next,直接看代码,没啥好说的,注意头节点可能为要删除节点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode deleteNode(ListNode head, int val) {
// 如果要删除的节点是头节点,特殊处理
if (head.val == val) return head.next;
// 删除的节点不是头节点
ListNode cur = head;
while (cur != null) {
if (cur.next.val == val) {
// 直接用next.next就能得到下下个节点
cur.next = cur.next.next;
break;
}
cur = cur.next;
}
return head;
}
}
19 正则表达式匹配


分析:用动态规划(Dynamic Programming,DP)
由于此题实在不会,找了一个好的题解放在这:


class Solution {
public boolean isMatch(String s, String p) {
int n = s.length();
int m = p.length();
boolean[][] dp = new boolean[n + 1][m + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= m; j++) {
// 空正则
if (j == 0) dp[i][j] = (i == 0);
// 非空正则
else {
// 最后一个字符不等于 '*'
if (p.charAt(j - 1) != '*') {
if (i > 0 && (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.')) dp[i][j] = dp[i - 1][j - 1];
} else {
// 下面的2种情况,都应该判断,而不是使用 else if 来连接
// 去除最后2个字符: '*' 和其前面的那个字符
if (j >= 2 && dp[i][j - 2]) dp[i][j] = dp[i][j - 2];
// 不去除最后2个字符:s 的最后一个字符等于 p 的最后一个 '*' 前面的字符
if (i >= 1 && j >= 2 && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') && dp[i - 1][j]) dp[i][j] = dp[i - 1][j];
}
}
}
}
return dp[n][m];
}
}
20 表示数值的字符串

分析:设置3个标志: numFlag,dotFlag,eFlag,然后遍历字符串的每个字符
- +(-)符号只能出现在首位或者e(E)后面,且+(-)后面必须紧跟数字
- 数字出现,则设置numFlag = true
- ‘.’ 只能出现一次,同时不能出现在e(E)后面,满足则设置dotFlag = true
- e(E)只能出现一次,且前面必须有数字,满足则设置eFlag = true
- 出现e(E)后,必须重新赋值numFlag = false,否则当出现"1e"这种情况,无法正确判定
- 其他字符的出现,直接return false
- 最后字符串能否表示数值,可以由numFlag来决定
class Solution {
public boolean isNumber(String s) {
// 去除前后的空格
s = s.trim();
boolean existNum = false;
boolean existDot = false;
boolean existE = false;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
// +(-)符号只能出现在首位或者e(E)后面,且+(-)如果位于e(E)后面的话,必须紧跟数字
if ((c == '+' || c == '-') && (i == 0 || s.charAt(i - 1) == 'e' || s.charAt(i - 1) == 'E')) {
// +(-)如果位于e(E)后面,必须紧跟数字,因此需要重新赋值 existNum = false
// existNum = false;
/*上面这条数据可以省略,当出现+(-)的时候,只有2种可能
1. i==0,就是符号出现在首位,这个时候+(-)后面可以跟 . 或者数字,所以此时 existNum 为 ture 或者 false 都没有影响
2. 符号前面是e(E),这个时候,+(-)后面必须紧跟数字,但是因为此时符号的前一个字符是e(E)的原因,在条件e(E)的else if语句里面
已经重新赋值了 existNum = false,因此不用再次赋值
*/
}
// .只能出现一次,同时不能出现在e(E)后面
else if (c == '.' && !existDot && !existE) existDot = true;
else if (c >= '0' && c <= '9') existNum = true; // 数字
// e(E)只能出现一次,且前面必须有数字出现
else if ((c == 'e' || c == 'E') && !existE && existNum) {
existE = true;
// 出现e(E)后,必须重新赋值numFlag = false,否则当出现"1e"这种情况,无法正确判定
existNum = false;
} else return false; // 其他字符的出现,直接return false
}
// 最后的结果,可以由numFlag来决定
return existNum;
}
}
21 调整数组顺序使奇数位于偶数前面

分析:遍历数组,将数组中的奇数依次按序全部放到前面,设置一个index = 0,如果此时的nums[i]为奇数,则与nums[index]的值交换位置,同时index++,即向后移动一位;如果此时nums[i]为偶数,则继续向后遍历,直到找到下一个奇数,然后和nums[index]交换位置,index++。
按位与运算,见上面15题:
一个数 &1 结果为0,则该数为偶数,否则为奇数。因为偶数的二进制最右边那位一定是0,而奇数的二进制最右边那位一定是1
class Solution {
public int[] exchange(int[] nums) {
// 方法1
int index = 0;
for (int i = 0; i < nums.length; i++) {
// 如果为奇数,跟 index 交换位置
if ((nums[i] & 1) != 0) {
int temp = nums[i];
nums[i] = nums[index];
nums[index] = temp;
index++;
}
}
return nums;
// 方法2:使用额外的数组:奇数从前面开始放,偶素从最后面开始放,此方法效率较低
// if (nums.length == 0) return new int[0];
// int[] arr = new int[nums.length];
// int left = 0;
// int right = nums.length - 1;
// for (int i = 0; i < nums.length; i++) {
// if (nums[i] % 2 == 0) arr[right--] = nums[i];
// else arr[left++] = nums[i];
// }
// return arr;
}
}
22 链表中倒数第k个节点

分析:首先,据提意,1应该理解为第1个节点而不是第0个节点。设置快慢双指针,首先让快指针指向第k + 1个指针,再让快慢2个指针同时移动,直到快指针为null,即指向最后一个指针的next时,慢指针此时则指向倒数第k个指针
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
// 使用双指针
ListNode pre = head;
ListNode cur = head;
while (k-- > 0) {
cur = cur.next;
}
while (cur != null) {
pre = pre.next;
cur = cur.next;
}
return pre;
}
}
24 反转链表

分析:设置一个新的链表用于存放反转后的链表,将正序链表里面的节点顺序遍历,依次把每一个节点倒序插入到新链表里面
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null) return head;
ListNode rHead = new ListNode(head.val);
rHead.next = null;
while (head.next != null) {
ListNode node = new ListNode(head.next.val);
node.next = rHead;
head = head.next;
rHead = node;
}
return rHead;
}
}
25 合并两个排序的链表
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// 合并链表节点
ListNode mNode = new ListNode(-1);
// 指向合并链表的当前节点
ListNode cur = mNode;
while (l1 != null && l2 != null) {
// 把 l1 和 l2 中较小的节点插到合并链表后面
if (l1.val < l2.val) {
cur.next = l1;
// 向后移动
l1 = l1.next;
} else {
cur.next = l2;
l2 = l2.next;
}
// 向后移动合并链表
cur = cur.next;
}
// 将 l1 或者 l2 后还有的节点全部直接插入到合并链表后面
cur.next = (l1 == null ? l2 : l1);
return mNode.next;
}
}
26 树的子结构


分析:运用递归,将树结构简化为root,left,right三个部分;比较B是否是A的子结构,如果不是,则比较B是否是A.left的子结构,如果也不是,则比较B是否是A.right的子结构
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
// 总体思路:先序遍历 A 的每一个节点,然后比较 B 是否是该节点所在子树的子结构
// 根据题意,空树不是任意一个树的子结构,同时当 A == null 的时候,也是遍历结束的时候
if (A == null || B == null) return false;
// 先序遍历:根节点
// 比较根节点值是否相等
if (A.val == B.val) {
// 调用方法比较 B 是否是 A 的子结构
if (helper(A, B)) return true;
}
// 先序遍历:左节点和右节点
// isSubStructure(A.left, B) 比较B是否是A.left的子结构
// isSubStructure(A.right, B) 比较B是否是A.right的子结构
return isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
public boolean helper(TreeNode A, TreeNode B) {
// 递归结束条件:如果 B = null,说明此时 B 已经比对完成,B 是 A 的子结构
if (B == null) return true;
// 递归结束条件:如果 A = null,说明此时 A 已经遍历完,但是 B 还存在节点未进行比对,B 不是 A 的子结构
if (A == null) return false;
if (A.val == B.val) {
// 如果 A,B 当前节点的值相等,则继续比对 A,B 左右节点是否相等
return helper(A.left, B.left) && helper(A.right, B.right);
}
return false;
}
}
27 二叉树的镜像
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode mirrorTree(TreeNode root) {
// 先序遍历,找到底部节点,然后交换左后子树位置
if (root == null) return root;
helper(root);
return root;
}
public void helper(TreeNode root) {
if (root == null) return;
helper(root.left);
helper(root.right);
// 交换左右子树位置
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
}
28 对称的二叉树


分析:利用递归,DFS从最底层的节点开始比较;此题不需要先求二叉树的镜像,再比较二叉树是否和镜像相同。可以直接利用二叉树本身实现
root.left == root.right;
root.right == root.left;
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
return compare(root.left, root.right);
}
public boolean compare(TreeNode nodeL, TreeNode nodeR) {
if (nodeL == null || nodeR == null) {
// 2个节点相同都为null,返回true,否则返回false
return nodeL == nodeR ? true : false;
}
// 如果2个节点值不同就返回 false
if (nodeL.val != nodeR.val) return false;
// 递归
return compare(nodeL.left, nodeR.right) && compare(nodeL.right, nodeR.left);
}
}
29 顺时针打印矩阵
class Solution {
public int[] spiralOrder(int[][] matrix) {
// 确定上下左右4个边界
if (matrix.length == 0) return new int[0];
// 左边界:列左边界
int left = 0;
// 右边界:列右边界
int right = matrix[0].length - 1;
// 上边界:行上边界
int top = 0;
// 下边界:行下边界
int bottom = matrix.length - 1;
int[] res = new int[matrix.length * matrix[0].length];
int index = 0;
while (true) {
// 向右移动
for (int i = left; i <= right; i++) res[index++] = matrix[top][i];
// 右移完成后:top++,上边界向下移动
if (++top > bottom) break;
// 向下移动
for (int j = top; j <= bottom; j++) res[index++] = matrix[j][right];
// 下移完成后,right--,右边界向左移动
if (left > --right) break;
// 向左移动
for (int m = right; m >= left; m--) res[index++] = matrix[bottom][m];
// 左移完成后,bottom--,下边界向上移动
if (top > --bottom) break;
// 向上移动
for (int n = bottom; n >= top; n--) res[index++] = matrix[n][left];
// 上移完成后,left++,左边界向右移动
if (++left > right) break;
}
return res;
}
}
30 包含min函数的栈
class MinStack {
// 使用辅助栈来保存最小值
private Stack<Integer> stack;
private Stack<Integer> stackMin;
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<>();
stackMin = new Stack<>();
}
public void push(int x) {
stack.push(x);
// 如果 stackMin 不为空,且 x <= stackMin 栈顶的值,则压入 stackMin 中
if (stackMin.empty() || x <= stackMin.peek()) stackMin.push(x);
}
public void pop() {
int m = stack.pop();
// 如果出栈的值 m == stackMin 栈顶的值,则弹出
if (!stackMin.empty() && (m == stackMin.peek())) stackMin.pop();
}
public int top() {
return stack.peek();
}
public int min() {
return stackMin.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(x);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.min();
*/
31 栈的压入、弹出序列
class Solution {
// 使用一个辅助栈
private Stack<Integer> stack = new Stack<>();
public boolean validateStackSequences(int[] pushed, int[] popped) {
int index = 0;
for (int i = 0; i < pushed.length; i++) {
// 入栈
stack.push(pushed[i]);
// 循环验证栈顶元素是否需要被弹出
while (!stack.empty() && popped[index] == stack.peek()) {
stack.pop();
index++;
}
}
return stack.empty();
}
}
32 - I 从上到下打印二叉树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int[] levelOrder(TreeNode root) {
// 题目要求的二叉树的 从上至下 打印(即按层打印),又称为二叉树的 广度优先搜索(BFS)
// BFS 通常借助 队列 的先入先出特性来实现
if (root == null) return new int[0];
// 这里定义集合来存取数据,因为此时不知道root有多少个节点,无法指定数组长度
List<Integer> list = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
// 如果不为 null,将该节点的值放入 list 集合,同时把此节点的左右子节点存入队列里面
if (node != null) {
list.add(node.val);
queue.offer(node.left);
queue.offer(node.right);
}
}
int[] res = new int[list.size()];
for (int i = 0; i < list.size(); i++) {
res[i] = list.get(i);
}
return res;
}
}
32 - II 从上到下打印二叉树 II
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if (root == null) return new ArrayList<List<Integer>>();
List<List<Integer>> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int length = queue.size();
// 初始化一个集合来存取当前层的数据
List<Integer> list = new ArrayList<>();
while (length-- > 0) {
TreeNode node = queue.poll();
if (node != null) {
list.add(node.val);
queue.offer(node.left);
queue.offer(node.right);
}
}
res.add(list);
}
// 最后一个位置保存的是空集合,需要手动去掉
res.remove(res.size() - 1);
return res;
}
}
32 - III 从上到下打印二叉树 III
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) return new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
// 使用双层List存储结果
List<List<Integer>> result = new ArrayList<>();
queue.add(root);
// 是否反转list标志
boolean flag = false;
while(!queue.isEmpty()) {
int length = queue.size();
// 初始化一个集合来存取当前层的数
List<Integer> list = new ArrayList<>();
while(length-- > 0) {
TreeNode node = queue.poll();
if(node == null) continue;
list.add(node.val);
queue.add(node.left);
queue.add(node.right);
}
// 反转列表
if(flag) Collections.reverse(list);
flag = !flag;
// 每一个while循环结束,就是遍历完一层树
result.add(list);
}
// 由于树的最后一层的节点的左右子节点还会被保存在队列中,进行遍历,因此还会产生一个空集合在最后,需要手动删除
result.remove(result.size() - 1);
return result;
}
}
方法2:使用 LinkedList 来反向插入数据
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int length = queue.size();
// 使用 LinkedList,便于反向插入数据
LinkedList<Integer> list = new LinkedList<>();
while (length-- > 0) {
TreeNode node = queue.poll();
if (node != null) {
// 奇数层逆向插入,偶数层正向插入
if ((res.size() & 1) == 1) list.addFirst(node.val);
else list.add(node.val);
queue.offer(node.left);
queue.offer(node.right);
}
}
res.add(list);
}
res.remove(res.size() - 1);
return res;
}
}
33 二叉搜索树的后序遍历序列

分析:二叉搜索树,则该树的左子树的所有节点值均小于根节点的值,而右子树的所有节点值均大于根节点的值
详解
class Solution {
public boolean verifyPostorder(int[] postorder) {
// 递归分治
if (postorder == null) return false;
return helper(postorder, 0, postorder.length - 1);
}
public boolean helper(int[] postorder, int left, int right) {
// 当 left >= right ,说明此子树节点数量 <= 1,无需判别正确性,因此直接返回 true
if (left >= right) return true;
int m = left;
while (postorder[m] < postorder[right]) m++;
int n = m;
while (postorder[n] > postorder[right]) n++;
return n == right && helper(postorder, left, m - 1) && helper(postorder, m, n - 1);
}
}
34 二叉树中和为某一值的路径
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// 回溯法
private List<List<Integer>> res = new ArrayList<>();
// 使用 LinkedList,删除效率更高
private LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
if (root == null) return res;
helper(root, target);
return res;
}
public void helper(TreeNode root, int target) {
if (root == null) return;
path.add(root.val);
target -= root.val;
// 注意必须到叶子节点
// 应该使用 new LinkedList(path) 复制一个列表,否则 path 最后会为空集合
if (target == 0 && root.left == null && root.right == null) res.add(new LinkedList(path));
helper(root.left, target);
helper(root.right, target);
// 回溯
path.removeLast();
}
}
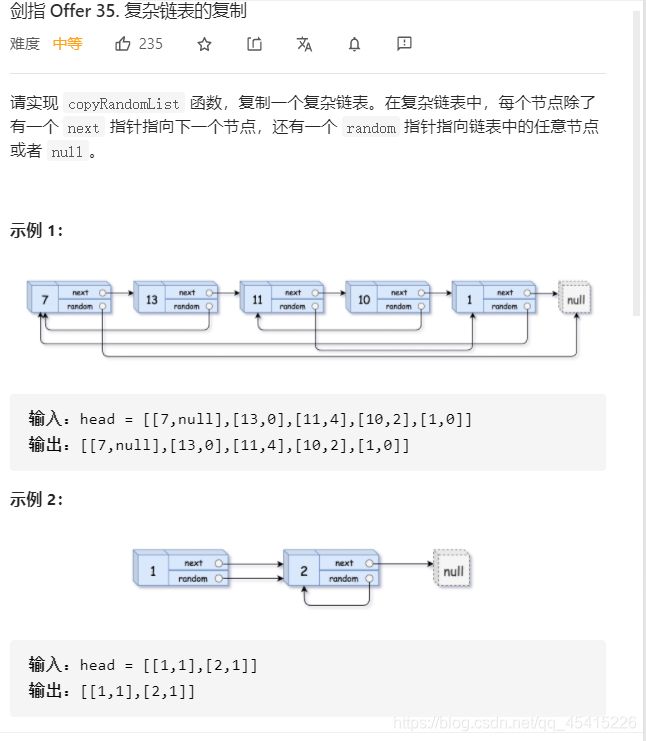
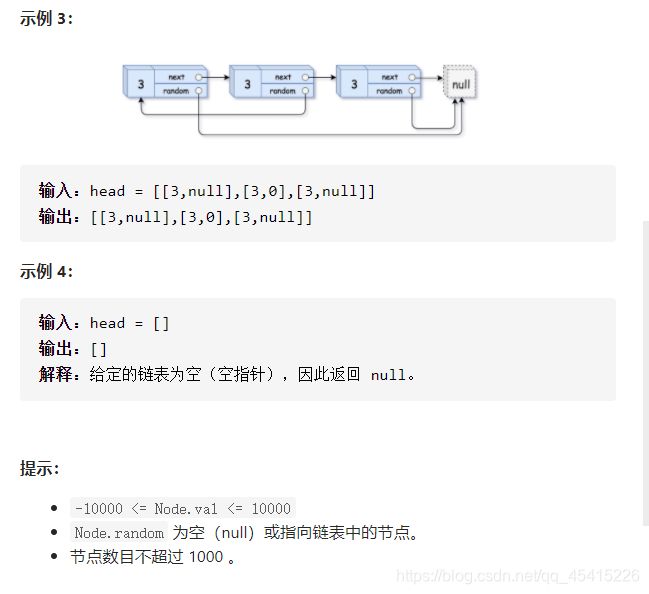
35 复杂链表的复制
/*
// Definition for a Node.
class Node {
int val;
Node next;
Node random;
public Node(int val) {
this.val = val;
this.next = null;
this.random = null;
}
}
*/
class Solution {
/* 这个题在原有链表基础上复制一个完全相同的链表出来,放在原有链表节点后面,最后进行拆分
当然,你可以直接return head,不过无法通过测试,因为会告诉你:不允许返回引用结果
"Node with label 7 was not copied but a reference to the original one."
百度翻译:未复制标签为7的节点,而是对原始节点的引用。
*/
public Node copyRandomList(Node head) {
// 方法1:使用 Hash 表:更易理解,但是空间效率较低
// if (head == null) return null;
// Map map = new HashMap<>();
// // 建立旧节点-新节点之间的对应关系
// Node cur = head;
// while (cur != null) {
// map.put(cur, new Node(cur.val));
// cur = cur.next;
// }
// cur = head;
// while (cur != null) {
// map.get(cur).next = map.get(cur.next);
// map.get(cur).random = map.get(cur.random);
// cur = cur.next;
// }
// return map.get(head);
// 方法2:拼接 + 拆分
if (head == null) return null;
// 拼接
Node cur = head;
while (cur != null) {
Node node = new Node(cur.val);
node.next = cur.next;
cur.next = node;
cur = node.next;
}
cur = head;
// next 和 random 指向
while (cur != null) {
if (cur.random != null) cur.next.random = cur.random.next;
cur = cur.next.next;
}
// 拆分
cur = head;
Node cloneNode = cur.next;
while (cur.next != null) {
Node node = cur.next;
cur.next = node.next;
cur = node;
}
return cloneNode;
}
}
36 二叉搜索树与双向链表
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val,Node _left,Node _right) {
val = _val;
left = _left;
right = _right;
}
};
*/
class Solution {
private Node head;
private Node pre;
public Node treeToDoublyList(Node root) {
if (root == null) return root;
helper(root);
head.left = pre;
pre.right = head;
return head;
}
public void helper(Node cur) {
if (cur == null) return;
// 遍历左子树
helper(cur.left);
// 如果前一个节点不为空,则将 pre 右节点指向当前节点
if (pre != null) pre.right = cur;
else head = cur;
// 让当前节点的左节点指向前一个节点
cur.left = pre;
// 更新pre节点为当前节点,即后移一个节点
pre = cur;
// 遍历右子树
helper(cur.right);
}
}
37 序列化二叉树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
// 层序遍历(BFS)
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) return "[]";
StringBuilder builder = new StringBuilder();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
builder.append("[");
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (node != null) {
builder.append(node.val + ",");
queue.offer(node.left);
queue.offer(node.right);
} else builder.append("null,");
}
// 删除最后位置的 ","
builder.deleteCharAt(builder.length() - 1);
builder.append("]");
return builder.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data.equals("[]")) return null;
String[] arr = data.substring(1, data.length() - 1).split(",");
Queue<TreeNode> queue = new LinkedList<>();
TreeNode root = new TreeNode(Integer.parseInt(arr[0]));
queue.offer(root);
int index = 1;
// 将非空节点加入队列中,同时遍历字符数组
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
if (!arr[index].equals("null")) {
node.left = new TreeNode(Integer.parseInt(arr[index]));
queue.offer(node.left);
}
index++;
if (!arr[index].equals("null")) {
node.right = new TreeNode(Integer.parseInt(arr[index]));
queue.offer(node.right);
}
index++;
}
return root;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));
38 字符串的排列
class Solution {
// 递归 + 回溯
private List<String> list = new ArrayList<>();
public String[] permutation(String s) {
// 把字符串转化为字符数组
char[] chars = s.toCharArray();
// 从小到大排序:这样可以让相同的字符挨在一起,对后序代码去重有用
Arrays.sort(chars);
// 标志字符数组是否已经被访问过
boolean[] visited = new boolean[s.length()];
// 递归
helper(chars, visited, "");
return list.toArray(new String[list.size()]);
}
public void helper(char[] chars, boolean[] visited, String str) {
// 如果chars长度 == 当前拼接的字符串长度,说明已经是某种顺序的字符串,list添加
if (str.length() == chars.length) {
list.add(str);
return;
}
// 遍历chars的每一个字符
for (int i = 0; i < chars.length; i++) {
if (visited[i]) continue;
// 如果此时不是第一个字符,并且和前一个字符相同,同时前一个字符还未被访问,或者说不包括在当前拼接好的字符串中
// 说明这种顺序的字符是重复的,直接跳过
if (i > 0 && chars[i] == chars[i - 1] && !visited[i - 1]) continue;
visited[i] = true;
// 拼接,同时在此基础上,继续向下拼接
helper(chars, visited, str + chars[i]);
// 回溯
visited[i] = false;
}
}
}
39 数组中出现次数超过一半的数字
class Solution {
public int majorityElement(int[] nums) {
// 摩尔投票
int res = 0;
int vote = 0;
for (int num : nums) {
if (vote == 0) res = num;
vote += (res == num ? 1 : -1);
}
return res;
}
}
40 最小的k个数
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
// 快速排序:哨兵划分 + 递归
quickSort(arr, 0, arr.length - 1);
return Arrays.copyOf(arr, k);
}
public void quickSort(int[] arr, int left, int right) {
if (left >= right) return;
int i = left;
int j = right;
// 哨兵划分
while (i < j) {
while (i < j && arr[j] >= arr[left]) j--;
while (i < j && arr[i] <= arr[left]) i++;
swap(arr, i, j);
}
swap(arr, i, left);
// 递归
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
41 数据流中的中位数
class MedianFinder {
private PriorityQueue<Integer> maxQueue;
private PriorityQueue<Integer> minQueue;
/** initialize your data structure here. */
public MedianFinder() {
// 大顶堆:从大 -> 小
maxQueue = new PriorityQueue(Collections.reverseOrder());
// 小顶堆:从小 -> 大
minQueue = new PriorityQueue();
}
public void addNum(int num) {
maxQueue.offer(num);
// 把大顶堆里面最大的值弹出,放入小顶堆里面
minQueue.offer(maxQueue.poll());
// 如果小顶堆元素总数较大,则把小顶堆里面最小的值弹出,放入大顶堆里面
if (minQueue.size() > maxQueue.size()) maxQueue.offer(minQueue.poll());
}
public double findMedian() {
return maxQueue.size() == minQueue.size() ? (minQueue.peek() + maxQueue.peek()) / 2.0 : maxQueue.peek() / 1.0;
}
}
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder obj = new MedianFinder();
* obj.addNum(num);
* double param_2 = obj.findMedian();
*/
42 连续子数组的最大和
class Solution {
public int maxSubArray(int[] nums) {
// 动态规划,dp[i] 保存以 nums[i] 结尾的最大连续子数组和
// 直接在 nums 数组上进行修改,降低空间复杂度
int max = nums[0];
for (int i = 1; i < nums.length; i++) {
nums[i] = nums[i - 1] > 0 ? nums[i] + nums[i - 1] : nums[i];
max = nums[i] > max ? nums[i] : max;
}
return max;
}
}
43 1~n整数中1出现的次数
class Solution {
public int countDigitOne(int n) {
// 递归
// 递归结束条件
if (n <= 0) return 0;
// 得到 n 的最高位
int high = String.valueOf(n).charAt(0) - '0';
// 计算 n 的量级,1233的量级为1000
int pow = (int)Math.pow(10, String.valueOf(n).length() - 1);
// 计算 n 去掉最高位的值
int last = n - high * pow;
// 2种情况,1 种 high = 1,其他情况 high != 1
if (high == 1) {
/*
n = 1233,high = 1,pow = 1000,last = 233,则1~n中出现1的次数分为3个部分:
1.只管最高位,为1:1000 - 1233 共有last + 1个1
2.只管非最高位,为1:0 - 999 共有countDigitOne(pow - 1)个1
3.last包括多少1,countDigitOne(last)
*/
return last + 1 + countDigitOne(pow - 1) + countDigitOne(last);
} else {
/*
n = 2233,high = 2,pow = 1000,last = 233,则1~n中出现1的次数分为3个部分:
1.只管最高位,为1:1000 - 1999 共有pow个1
2.只管非最高位,为1:0 - 999 共有high * countDigitOne(pow - 1)个1
3.last包括多少1,countDigitOne(last)
*/
return pow + high * countDigitOne(pow - 1) + countDigitOne(last);
}
}
}
44 数字序列中某一位的数字
class Solution {
public int findNthDigit(int n) {
if (n < 10) return n;
// 临时变量,保存当前 pow 以前的各段值和
long temp = 10;
// 每段的量级
int pow = 2;
// 各段值和
long sum = 10;
while (true) {
sum += helper(pow);
if (n < sum) {
n -= temp;
int x = (int)Math.pow(10, pow - 1) + n / pow;
return String.valueOf(x).charAt(n % pow) - '0';
}
temp = sum;
pow++;
}
}
public long helper(int pow) {
return (long)Math.pow(10, pow - 1) * 9 * pow;
}
}
45 把数组排成最小的数
class Solution {
// 方法1
// public String minNumber(int[] nums) {
// String[] arr = new String[nums.length];
// for (int i = 0; i < nums.length; i++) {
// arr[i] = String.valueOf(nums[i]);
// }
// // 使用内置函数排序
// Arrays.sort(arr, new Comparator() {
// public int compare(String o1, String o2) {
// return (o1 + o2).compareTo(o2 + o1);
// }
// });
// StringBuilder builder = new StringBuilder();
// for (String str : arr) builder.append(str);
// return builder.toString();
// }
// 方法2:快排
public String minNumber(int[] nums) {
// 快速排序:比较 x y -> x + y > y + x (字符串)
String[] arr = new String[nums.length];
for (int i = 0; i < nums.length; i++) {
arr[i] = String.valueOf(nums[i]);
}
quickSort(arr, 0, arr.length - 1);
StringBuilder builder = new StringBuilder();
for (String str : arr) builder.append(str);
return builder.toString();
}
public void quickSort(String[] arr, int left, int right) {
if (left >= right) return;
int i = left;
int j = right;
String temp = null;
while (i < j) {
// 从右往左找出小于 left 位置的元素下标
while (i < j && (arr[j] + arr[left]).compareTo(arr[left] + arr[j]) >= 0) j--;
// 从左往右找出大于 left 位置的元素下标
while (i < j && (arr[i] + arr[left]).compareTo(arr[left] + arr[i]) <= 0) i++;
// 交换 i j 位置
temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
// 交换 i left 位置
arr[i] = arr[left];
arr[left] = temp;
// 递归排序左部分
quickSort(arr, left, i - 1);
// 递归排序右部分
quickSort(arr, i + 1, right);
}
}
46 把数字翻译成字符串
class Solution {
public int translateNum(int num) {
// dp[i] 表示 i 位数字共有多少种不同的翻译方法
// 例如 123 共有下述3种情况
// A. bcd(1 2 3)
// B. md(12 3)
// C. bx(1 23)
// 这3种情况其实可以归纳为2种:最后1位数字3,是否和前一位数字构成1个符合条件的2位数
// E. 不和前一位数字构成2位数:A、B 2种情况;
// F. 和前一位数字构成一个符合条件的2位数:C 1种情况
// 所以有 dp[i] = dp[i - 2] + dp[i - 1]
// dp[i - 1]可以视为第一种情况E;dp[i - 2]可以视为第二种情况F
String str = String.valueOf(num);
int length = str.length();
int[] dp = new int[length + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= length; i++) {
dp[i] = dp[i - 1];
int m = (str.charAt(i - 2) - '0') * 10 + (str.charAt(i - 1) - '0');
// 注意:判定范围应该是 10 - 25,例如:106中06无法构成一个新的字母
if (m >=10 && m <= 25) dp[i] += dp[i - 2];
}
return dp[length];
}
}
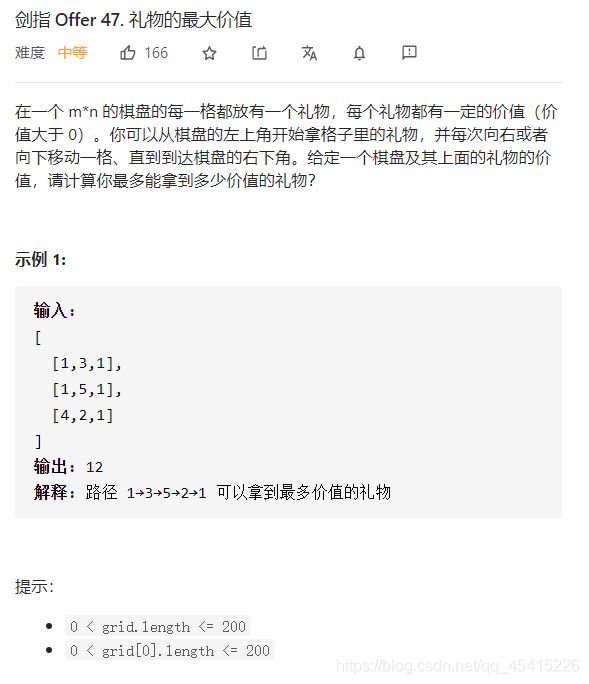
47 礼物的最大价值
class Solution {
public int maxValue(int[][] grid) {
// 动态规划:原地修改使用常数大小的额外空间
// 第0行的礼物价值,向右递增即可
for (int i = 1; i < grid[0].length; i++) grid[0][i] += grid[0][i - 1];
// 第0列的礼物价值,向下递增即可
for (int j = 1; j < grid.length; j++) grid[j][0] += grid[j - 1][0];
// 然后直接从第1行1列位置开始计算最大礼物价值
for (int i = 1; i < grid.length; i++) {
for (int j = 1; j < grid[0].length; j++) {
grid[i][j] += (int)Math.max(grid[i][j - 1], grid[i - 1][j]);
}
}
return grid[grid.length - 1][grid[0].length - 1];
}
}
48 最长不含重复字符的子字符串
class Solution {
public int lengthOfLongestSubstring(String s) {
// 方法1:使用滑动窗口
// if (s == null) return 0;
// Set set = new HashSet<>();
// int left = 0;
// int right = 0;
// int max = 0;
// int length = s.length();
// while (left < length && right < length) {
// if (set.contains(s.charAt(right))) {
// set.remove(s.charAt(left++));
// } else {
// set.add(s.charAt(right++));
// max = (int)Math.max(max, right - left);
// }
// }
// return max;
// 方法2:效率更好,但是不太好理解,建议使用方法1
// 用1个数组来保存字符出现位置的下一个下标,如果有重复的字符出现,则左边界跳转到重复值原来字符的下一个位置
int length = s.length();
int[] arr = new int[128];
int max = 0;
for (int left = 0, right = 0; right < length; right++) {
// 更新左边界
left = (int)Math.max(arr[s.charAt(right)], left);
max = (int)Math.max(max, right - left + 1);
arr[s.charAt(right)] = right + 1;
}
return max;
}
}
49 丑数
class Solution {
public int nthUglyNumber(int n) {
// 动态规划
int[] dp = new int[n];
dp[0] = 1;
int a = 0;
int b = 0;
int c = 0;
for (int i = 1; i < n; i++) {
dp[i] = Math.min(dp[a] * 2, Math.min(dp[b] * 3, dp[c] * 5));
if (dp[a] * 2 == dp[i]) a++;
if (dp[b] * 3 == dp[i]) b++;
if (dp[c] * 5 == dp[i]) c++;
}
return dp[n - 1];
}
}
50 第一个只出现一次的字符
class Solution {
public char firstUniqChar(String s) {
// 方法1:调用 String API 效率较低
// if(s.equals("")) return ' ';
// for(int i = 0; i < s.length(); i++) {
// int start = s.indexOf(s.charAt(i));
// int end = s.lastIndexOf(s.charAt(i));
// if(start == end) return s.charAt(i);
// }
// return ' ';
// }
// 方法2:使用一个数组来记录字符出现的次数
int[] map = new int[128];
int length = s.length();
for (int i = 0; i < length; i++) {
map[s.charAt(i)]++;
}
for (int j = 0; j < length; j++) {
if (map[s.charAt(j)] == 1) return s.charAt(j);
}
return ' ';
}
}
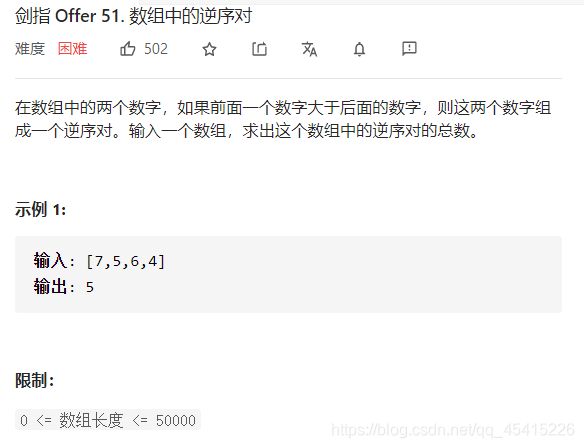
51 数组中的逆序对
class Solution {
private int[] nums;
private int[] temps;
public int reversePairs(int[] nums) {
// 归并排序
this.nums = nums;
temps = new int[nums.length];
return mergeSort(0, nums.length - 1);
}
public int mergeSort(int left, int right) {
if (left >= right) return 0;
int mid = (left + right) / 2;
int res = mergeSort(left, mid) + mergeSort(mid + 1, right);
// 使用i j 分别指向左右两部分数组的头部位置
int i = left;
int j = mid + 1;
// 给临时数组赋值
for (int k = left; k <= right; k++) {
temps[k] = nums[k];
}
for (int m = left; m <= right; m++) {
// 如果左半部分数组比对完,直接将右半部分剩余数组插入后面
if (i == mid + 1) nums[m] = temps[j++];
// 如果右半部分数组比对完,直接将左半部分剩余数组插入后面;或者左边的数小于等于右边的数,将左边小的数插入
else if (j == right + 1 || temps[i] <= temps[j]) nums[m] = temps[i++];
// 如果左边的数大于右边的数,则将右边小的数插入,同时计算逆序对
else {
nums[m] = temps[j++];
res += (mid - i + 1);
}
}
return res;
}
}
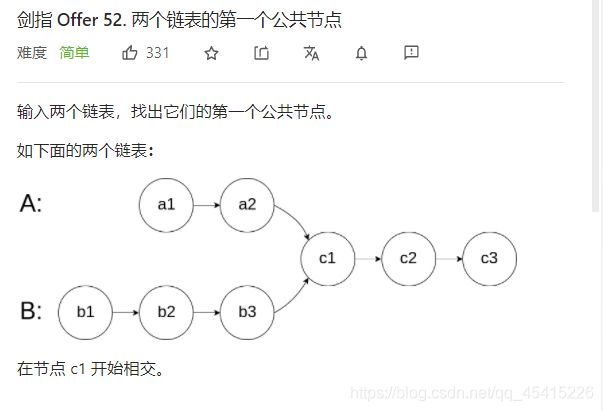
52 两个链表的第一个公共节点
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
// 两个链表长度分别为L1+C、L2+C, C为公共部分的长度
// 第一个人走了L1+C步后,回到第二个人起点走L2步;第2个人走了L2+C步后,
// 回到 第一个人起点走L1步。当两个人走的步数都为L1+L2+C时就到公共节点了
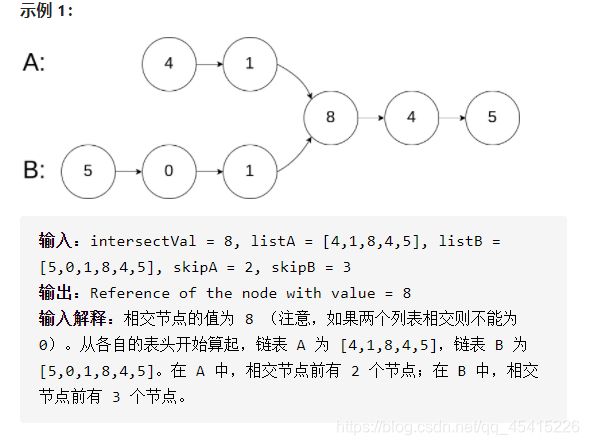
// 示例1:为什么第一个公共节点不是1?
// 因为对于包装类型 == 比较的是地址,在初始化headA和headB的时候,应该节点1的地址是不同的
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode nodeA = headA;
ListNode nodeB = headB;
while (nodeA != null || nodeB != null) {
if (nodeA == nodeB) return nodeA;
nodeA = nodeA == null ? headB : nodeA.next;
nodeB = nodeB == null ? headA : nodeB.next;
}
return null;
}
}
53- I 在排序数组中查找数字
class Solution {
public int search(int[] nums, int target) {
// 二分法
int left = 0;
int right = nums.length - 1;
int mid = 0;
while (left <= right) {
mid = (left + right) / 2;
if (nums[mid] > target) right = --mid;
else if (nums[mid] < target) left = ++mid;
else {
left = mid;
right = mid;
// 向前遍历
while (left >= 0 && nums[left] == target) left--;
// 向后遍历
while (right < nums.length && nums[right] == target) right++;
return right - left - 1;
}
}
return 0;
}
}
53-II 0~n-1中缺失的数字
class Solution {
public int missingNumber(int[] nums) {
// 方法1:直接遍历,此种方法时间复杂度为:O(N)
// for (int i = 0; i < nums.length; i++) {
// if (i != nums[i]) return i;
// }
// return nums.length;
// 方法2:二分法,时间复杂度为:O(log2N) 更快
// int left = 0;
// int right = nums.length - 1;
// while (left <= right) {
// int mid = (left + right) / 2;
// if (nums[mid] > mid) right = --mid;
// else left = ++mid;
// }
// return left;
// 方法3:使用异或操作
int res = 0;
for (int i = 0; i < nums.length; i++) {
res ^= (i ^ nums[i]);
}
return res ^ nums.length;
}
}
54 二叉搜索树的第k大节点
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int res;
int k;
public int kthLargest(TreeNode root, int k) {
this.k = k;
// 中序遍历
helper(root);
return res;
}
public void helper(TreeNode root) {
if (root == null) return;
// 先放右节点,实现逆序
helper(root.right);
if (--k == 0) {
res = root.val;
return;
}
helper(root.left);
}
}
55-I 二叉树的深度
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
// 递归:效率更高
// if (root == null) return 0;
// return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
// 层序遍历
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while (!queue.isEmpty()) {
int length = queue.size();
while (length-- > 0) {
TreeNode node = queue.poll();
if (node != null) {
queue.offer(node.left);
queue.offer(node.right);
}
}
depth++;
}
return --depth;
}
}
55-II 平衡二叉树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean isBalanced(TreeNode root) {
// 后序遍历
return helper(root) == -1 ? false : true;
}
public int helper(TreeNode root) {
if (root == null) return 0;
int left = helper(root.left);
if (left == -1) return -1;
int right = helper(root.right);
if (right == -1) return -1;
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
56-I 数组中数字出现的次数
class Solution {
public int[] singleNumbers(int[] nums) {
int[] res = new int[2];
int m = 0;
for (int num : nums) {
m ^= num;
}
int n = 1;
while ((m & n) == 0) {
n <<= 1;
}
for (int num : nums) {
if ((num & n) == 0) res[0] ^= num;
else res[1] ^= num;
}
return res;
}
}
56-II 数组中数字出现的次数 II
class Solution {
public int singleNumber(int[] nums) {
// 遍历二进制位
int[] count = new int[32];
for (int num : nums) {
// 将 32 位形式的 num 进行计数统计
for (int i = 0; i < 32; i++) {
count[i] += (num & 1);
// 无符号右移,高位补 0
num >>>= 1;
}
}
int res = 0;
for (int i = 31; i >= 0; i--) {
// 左移 1 位
res <<= 1;
res |= (count[i] % 3);
}
return res;
}
}
57 和为s的两个数字
class Solution {
public int[] twoSum(int[] nums, int target) {
// 使用双指针分别从头尾向中间移动
// 如果nums[left] + nums[right] > target,则尾部指针向前移动
// 如果nums[left] + nums[right] < target,则头部指针向后移动
// 如果相等了,直接返回
int left = 0;
int right = nums.length - 1;
while (left < right) {
if (nums[left] + nums[right] > target) right--;
else if (nums[left] + nums[right] < target) left++;
else return new int[]{nums[left], nums[right]};
}
return new int[0];
}
}
57-II 和为s的连续正整数序列
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> res = new ArrayList<>();
int m = (target + 1) / 2;
int left = 1;
int right = 1;
int sum = 0;
while (right <= m) {
while (sum < target) sum += right++;
while (sum > target) sum -= left++;
if (sum == target) {
int[] arr = new int[right - left];
for (int i = left; i < right; i++) {
arr[i - left] = i;
}
res.add(arr);
sum -= left++;
}
}
return res.toArray(new int[0][]);
}
}
58-I 翻转单词顺序
class Solution {
public String reverseWords(String s) {
// 倒序遍历字符串 s ,记录单词左右索引边界 i , j
// 每确定一个单词的边界,则将其添加至单词列表 res
// 最终,将单词列表拼接为字符串,并返回即可
// 双指针
s = s.trim();
int left = s.length() - 1;
int right = left;
StringBuilder builder = new StringBuilder();
while (left >= 0) {
// 搜索不为空的字符串左边界
while (left >= 0 && s.charAt(left) != ' ') left--;
// 添加字符串
builder.append(s.substring(left + 1, right + 1) + " ");
// 跳过空格
while (left >= 0 && s.charAt(left) == ' ') left--;
right = left;
}
return builder.toString().trim();
}
}
58-II 左旋转字符串
class Solution {
public String reverseLeftWords(String s, int n) {
// 截取对应位置然后拼接即可
return s.substring(n) + s.substring(0, n);
}
}
59-I 滑动窗口的最大值
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 0) return new int[0];
// 使用双端队列,队首保存最大值,同时新增一个元素,需要去除掉原队列里所有小于该新增元素的值,维护一个递减队列
Deque<Integer> deque = new LinkedList<>();
List<Integer> list = new ArrayList<>();
// 未形成窗口
for (int i = 0; i < k; i++) {
while (!deque.isEmpty() && nums[i] > deque.peekLast()) deque.pollLast();
deque.offer(nums[i]);
}
list.add(deque.peek());
// 形成窗口
for (int j = k; j < nums.length; j++) {
// 如果即将去掉的窗口左侧数等于队列的队首(即最大值),需要去除队列的队首
if (nums[j - k] == deque.peek()) deque.poll();
while (!deque.isEmpty() && nums[j] > deque.peekLast()) deque.pollLast();
deque.offer(nums[j]);
list.add(deque.peek());
}
int[] res = new int[list.size()];
int length = list.size();
for (int i = 0; i < length; i++) res[i] = list.get(i);
return res;
}
}
59-II 队列的最大值
class MaxQueue {
private Queue<Integer> queue;
// 使用双端队列,可以取出队尾的元素
private Deque<Integer> deque;
public MaxQueue() {
queue = new LinkedList<>();
deque = new LinkedList<>();
}
public int max_value() {
if (queue.isEmpty()) return -1;
return deque.peek();
}
public void push_back(int value) {
queue.offer(value);
// 这道题思路核心是下面这行代码
// 如果新添元素大于队列尾部元素,则移除所有小于新添元素的值
while (!deque.isEmpty() && deque.peekLast() < value) deque.pollLast();
deque.offer(value);
}
public int pop_front() {
if (queue.isEmpty()) return -1;
// 如果移除元素等于双端队列的头元素,则也需要同时移除
if (queue.peek().equals(deque.peek())) deque.poll();
return queue.poll();
}
}
/**
* Your MaxQueue object will be instantiated and called as such:
* MaxQueue obj = new MaxQueue();
* int param_1 = obj.max_value();
* obj.push_back(value);
* int param_3 = obj.pop_front();
*/
60 n个骰子的点数
class Solution {
public double[] dicesProbability(int n) {
// 对于n个骰子,出现的点数范围是:n - 6n,所以共有 6n - n + 1 种点数可能
double[] res = new double[5 * n + 1];
// 二维数组:行为骰子个数,列为骰子个数对应出现的点数可能
double[][] dp = new double[n + 1][6 * n + 1];
// 骰子个数为1的时候,概率确定 1/6
for(int r = 1; r <= 6; r++) {
dp[1][r] = 1.0 / 6.0;
}
// 骰子的个数
for (int i = 2; i <= n ;i++) {
// 骰子个数为 i 时,对应的点数范围
for (int j = i; j <= 6 * i; j++) {
// 对于每一个点数的概率,取决于前 i - 1 个骰子和第 i 个骰子
// 第 i 个骰子只有可能是 1 - 6 并且每个点数的概率都是 1/6
for(int k = 1; k <= 6; k++) {
if(j - k <= 0) break;
dp[i][j] += dp[i - 1][j - k] / 6.0;
}
}
}
// 返回 n 个骰子出现的点数概率
for(int m = 0; m <= 5 * n; m++) {
res[m] = dp[n][n + m];
}
return res;
// 优化代码
// double[] dp = new double[6];
// Arrays.fill(dp, 1 / 6.0);
// for (int i = 2; i <= n; i++) {
// double[] temp = new double[5 * i + 1];
// for (int j = 0; j < dp.length; j++) {
// for (int m = 0; m < 6; m++) {
// temp[j + m] += dp[j] / 6.0;
// }
// }
// dp = temp;
// }
// return dp;
}
}
61 扑克牌中的顺子
class Solution {
public boolean isStraight(int[] nums) {
// 排序:从小到大
Arrays.sort(nums);
int count = 0;
for (int i = 0; i < nums.length - 1; i++) {
if (nums[i] == 0) count++;
else if (nums[i] == nums[i + 1]) return false;
}
// 如果最大值 - 最小值 < 5(大小王除外),符合条件
return nums[nums.length - 1] - nums[count] < 5;
}
}
62 圆圈中最后剩下的数字
class Solution {
public int lastRemaining(int n, int m) {
// 数学方法:最后所剩数字在上一轮中的下标 = (当前下标 + m) % 上一轮数字的个数
int index = 0;
for (int i = 2; i <= n; i++) {
index = (index + m) % i;
}
// 下标即为最后一个数字
return index;
}
}
63 股票的最大利润
class Solution {
public int maxProfit(int[] prices) {
// 动态规划,第 n 天最大利润 = Max(前 n-1 天的最大利润,当前股票价格 - 前 n - 1天股票价格的最小值)
int profit = 0;
int min = Integer.MAX_VALUE;
for (int price : prices) {
min = Math.min(price, min);
profit = Math.max(price - min, profit);
}
return profit;
}
}
64 求1+2+…+n
class Solution {
public int sumNums(int n) {
// 使用短路与来解决条件终止问题
boolean x = n > 1 && (n += sumNums(n - 1)) > 0;
return n;
}
}
65 不用加减乘除做加法
class Solution {
public int add(int a, int b) {
// 拆分成进位和 + 非进位和
// 当进位和等于 0 的时候,非进位和即为两个整数之和
while (a != 0) {
int temp = a;
// 进位和
a = (a & b) << 1;
// 非进位和
b ^= temp;
}
return b;
}
}
66 构建乘积数组
class Solution {
public int[] constructArr(int[] a) {
int length = a.length;
// 长度小于2,直接返回
if (length < 2) return new int[0];
int[] res = new int[length];
int tmp = 1;
res[0] = 1;
// 正序循环遍历下三角
for (int i = 1; i < length; i++) {
res[i] = res[i - 1] * a[i - 1];
}
// 逆序循环遍历上三角
for (int j = length - 2; j >= 0; j--) {
tmp *= a[j + 1];
res[j] *= tmp;
}
return res;
}
}
67 把字符串转化成整数
class Solution {
public int strToInt(String str) {
// 空间复杂度 O(N):删除首尾空格后需建立新字符串,最差情况下占用 O(N) 额外空间。
// str = str.trim();
// 不使用 trim() 函数来降低空间复杂度
int length = str.length();
if (length == 0) return 0;
int index = 0;
while (str.charAt(index) == ' ') {
if (++index == length) return 0;
}
int sign = 1;
if (str.charAt(index) == '-') {
sign = -1;
index++;
} else if (str.charAt(index) == '+') index++;
int res = 0;
int num = Integer.MAX_VALUE / 10;
for (int i = index; i < length; i++) {
if (str.charAt(i) < '0' || str.charAt(i) > '9') break;
if (res > num || (res == num && str.charAt(i) > '7')) return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
res = res * 10 + (str.charAt(i) - '0');
}
return res * sign;
}
}
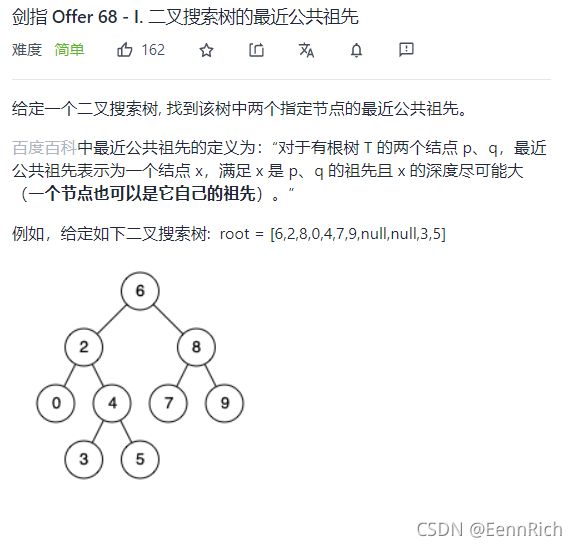
68 - I 二叉搜索树的最近公共祖先
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
// public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// // 迭代法
// // 保证 p.val < q.val,减少 while 中的判断次数
// if (p.val > q.val) {
// TreeNode tmp = p;
// p = q;
// q = tmp;
// }
// while (root != null) {
// // p,q 都在右子树中
// if (root.val < p.val) root = root.right;
// // p,q 都在左子树中
// else if (root.val > q.val) root = root.left;
// // 都不满足,说明此时root就是最近公共祖先
// else break;
// }
// return root;
// }
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 递归
// 保证 p.val < q.val,减少判断次数
if (p.val > q.val) {
TreeNode tmp = p;
p = q;
q = tmp;
}
return helper(root, p ,q);
}
private TreeNode helper(TreeNode root, TreeNode p, TreeNode q) {
if (root.val < p.val) return helper(root.right, p, q);
else if (root.val > q.val) return helper(root.left, p, q);
return root;
}
}
68 - II 二叉搜索树的最近公共祖先
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 递归先序遍历该二叉树
if (root == null || root == p || root ==q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left == null) return right;
if (right == null) return left;
return root;
}
}