为何红黑树在B/B+树之上仍然占据重要地位？

博主简介

---

一个热爱分享高性能服务器后台开发知识的博主，目标是通过理论与代码实践的结合，让世界上看似难以掌握的技术变得易于理解与掌握。技能涵盖了多个领域，包括C/C++、Linux、数据结构与算法、Nginx、MySQL、Redis、fastdfs、kafka、Docker、TCP/IP、协程、DPDK等。

️ CSDN实力新星、CSDN博客专家、华为云云享专家、阿里云专家博主

---

引言

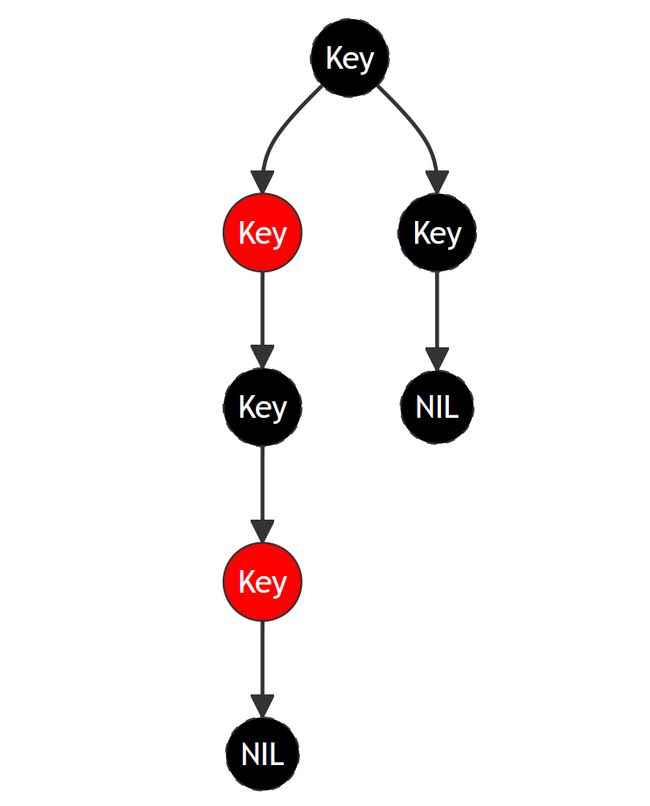
红黑树是一种具有平衡性质的二叉搜索树，它通过将节点着色为红色或黑色，并通过一组特定的规则来保持树的平衡。

• 每个结点是红的或者黑的。
• 根结点是黑的。
• 每个叶子结点是黑的。
• 如果一个结点是红的，则它的两个儿子都是黑的。
• 对每个结点，从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点 。

红黑树的平衡性能能够保证在最坏情况下的操作（插入、删除、查找）时间复杂度为O(log n)。

B/B+树是一种多路搜索树，主要用于在磁盘或其他多级存储介质上组织和管理大规模数据。一颗M阶B树T，满足以下条件：

• 每个结点至多拥有M颗子树。
• 根结点至少拥有两颗子树。
• 除了根结点以外，其余每个分支结点至少拥有M/2课子树。
• 所有的叶结点都在同一层上。
• 有k课子树的分支结点则存在k-1个关键字，关键字按照递增顺序进行排序。
• 关键字数量满足ceil(M/2)-1 <= n <= M-1。

B/B+树的平衡特性使得在大规模数据的增删改查操作中，其磁盘IO次数相对较少，能够提供更高的效率。

红黑树在数据结构中占据重要地位的原因包括其平衡性能、适用于索引结构、广泛应用于算法和数据处理，以及相对简单的实现方式。

1. 红黑树在最坏情况下，红黑树的插入、删除和查找操作的时间复杂度都是O(log n)。
2. 红黑树在算法和数据处理中广泛应用。例如，在图算法中，红黑树被用于存储顶点和边的关系，3. 以快速搜索和遍历图结构。
3. 相对于其他平衡二叉搜索树数据结构，红黑树的实现方式相对简单。

二、红黑树和B/B+树的基本原理

2.1、红黑树的特点和性质

红黑树在二叉树的基础上具备如下的性质：

• 每个结点是红的或者黑的。
• 根结点是黑的。
• 每个叶子结点是黑的。
• 如果一个结点是红的，则它的两个儿子都是黑的。
• 对每个结点，从该结点到其子孙结点的所有路径上的 包含相同数目的黑结点 。

满足以上性质的二叉树就是红黑树。其中第五条性质就决定了红黑树的平衡，它不像AVL树那样严格要求两边子树的高度差是1，而是要求黑色节点的高度一致即可。

从第四条和第五条的性质中，我们可以总结出一个数学结论：红黑树的根节点到叶子节点的最短路径与红黑树的根节点到叶子节点的最长路径之比是 $1:(2\times N-1)$。

2.2、B/B+树的特点和性质

对上面的六个性质进行精简描述一下：

• 树开叉的数量上限是M颗，也就是定义了范围。
• 形容M颗子树与Key值的关系。
• 所有的叶子节点在同一层。
• 除了根节点以外，每个节点最少有 $M÷2$ 颗子树。

在这里再扩展一些知识：

• B-tree / B tree：这种名称定义都是说的B树，不存在B"减"树这个数据结构。
• B+tree：B树的所有节点都是存储数据的，B+树是B树的扩展或者变种，B+树的内节点不存储数据，只做索引，所有的数据都存储在叶子节点。此外，B+树适合范围查阅是由链表性质决定的。
• B+树更适合做磁盘索引，性能优于B树；因为B+树的内结点不存储数据。同样的内存空间，B树的结点除了要存储key值，还要存储value值，所以B树的节点会比B+树的节点内存占用大，从而存储B树的节点会少于B+树的节点。

B树和B+树在使用场景上的差异说明：举个例子，假设有一个很大量的数据需要存储（比如100万个节点），内存上肯定无法全部存储，必然有很大部分在磁盘上。

• 如果使用B树进行存储，由于每个节点都存储数据，必然有一部分节点存储在内存中，一部分节点存储在磁盘上。

• 如果使用B+树存储，就有些不一样，由于B+树的内节点不存储具体数据，只做索引，所以B+树存储在内存中的节点数量会比B树多得多。所以，B+树做索引会更好，因为可以把所有的索引关系存储到内存中，然后通过一次性寻址找到存储具体数据的叶子节点。B树就无法做到这样，它只能一个节点一个节点的磁盘寻址。

B树和B+树都可以做索引，但是B+树更常用于做索引，特别是索引磁盘数据。比如MySQL、mongodb、PostgreSql等数据库的索引使用的就是B+树。

2.3、红黑树和B/B+树的比较

红黑树对于范围查询操作不如B/B+树高效。在红黑树中，需要进行中序遍历才能获取范围内的键值。B/B+树内部节点通过键值范围进行连接，因此在范围查询时，只需遍历相应的叶子节点链表即可，效率更高。

红黑树适用于内存中的高效搜索和平衡需求，而B/B+树适用于大规模数据的组织和管理，特别是在磁盘或其他多级存储介质中。

三、B/B+树相对于红黑树的优势

B/B+树在存储效率、范围查询效率、磁盘I/O优化、顺序访问性能以及分裂和合并操作效率等方面具有优势。这使得B/B+树成为在磁盘或其他多级存储介质上管理和组织大规模数据的一种重要的数据结构。

1. B/B+树的节点可以存储多个键和对应的值，相比红黑树，每个节点能够容纳更多的数据。这样就减少了节点的数量，降低了存储空间的开销。
2. B/B+树的内部节点通过键值范围进行连接，并且叶子节点通过链表连接在一起。这种结构的特点使得范围查询操作非常高效。只需遍历相应的叶子节点链表，而不需要像红黑树一样对整棵树进行中序遍历。
3. B/B+树常用于在磁盘或其他多级存储介质上组织和管理大规模数据。B/B+树的分层结构使得在查找数据时只需进行少量的磁盘I/O操作，大大提高了访问速度。
4. B/B+树中的键是按顺序存储的，这使得对数据的顺序访问效率非常高。对于需要顺序访问或顺序扫描大量数据的场景，B/B+树是一个很好的选择。

四、红黑树仍然占据重要地位的原因

• 在最坏情况下，红黑树的插入、删除和查找操作的时间复杂度都是O(log n)，对于需要快速的搜索和排序操作的场景非常重要。
• 许多重要的数据结构和算法都是基于红黑树实现的，包括数据库系统、文件系统、编译器、图算法等。
• 红黑树的实现比较简单。
• 红黑树的性质非常稳定，插入和删除操作不会频繁地改变整棵树的结构。
• 红黑树经过了充分验证和优化，已存在许多成熟的实现和优化方案。

总结

尽管红黑树可能导致树的高度相对较高，但其存储效率、数据局部性、平衡性能和范围查询效率等特点在内存中或需要更好的数据局部性时，红黑树更好。

1. 相比B树或B+树，红黑树的节点结构相对简单，每个节点只需额外存储一个颜色位。
2. 红黑树在插入和删除操作时能够通过旋转和重新着色来保持平衡性质。相比之下，B树或B+树的平衡调整操作（如节点的分裂和合并）可能更复杂。