滑动窗口技巧
文章目录
- 1. 最小覆盖子串
- 2. 字符串排列
- 3. 找所有字母异位词
- 4. 最长无重复子串
- 5. 最后总结
- 6. 题型训练
本文详解「滑动窗口」这种 高级双指针技巧 的算法框架,带你秒杀几道高难度的 子字符串匹配问题 (也就是说在遇到子字符串匹配的时候需要用到滑动窗口?注意区分子字符串和子序列的概念)。
LeetCode 上至少有 9 道题目可以用此方法高效解决。但是有几道是 VIP 题目,有几道题目虽不难但太复杂,所以本文只选择点赞最高,较为经典的,最能够讲明白的三道题来讲解。第一题为了让读者掌握算法模板,篇幅相对长,后两题就基本秒杀了。该算法的大致逻辑如下:
int left = 0, right = 0;
while (right < s.size()) {
// 1. 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 2. 缩小窗口
window.remove(s[left]);
left++;
}
}
这个算法技巧的时间复杂度是 O ( N ) O(N) O(N),比一般的字符串暴力算法要高效得多。
其实困扰大家的,不是算法的思路,而是各种细节问题。 比如说如何向窗口中添加新元素,如何缩小窗口,在窗口滑动的哪个阶段更新结果。即便你明白了这些细节,也容易出 bug,找 bug 还不知道怎么找,真的挺让人心烦的。
所以今天我就写一套滑动窗口算法的代码框架,我连在哪里做输出 debug 都给你写好了,以后遇到相关的问题,你就默写出来如下框架然后改三个地方就行,还不会出边界问题:
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
/*** debug 输出的位置 ***/
printf("window: [%d, %d)\n", left, right);
/********************/
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}
其中两处...表示的更新窗口数据的地方,到时候你直接往里面填就行了。
而且,这两个...处的操作分别是右移和左移窗口更新操作,等会你会发现它们操作是完全对称的。
说句题外话,其实有很多人喜欢执着于表象,不喜欢探求问题的本质。比如说有很多人评论我这个框架,说什么散列表速度慢,不如用数组代替散列表;还有很多人喜欢把代码写得特别短小,说我这样代码太多余,影响编译速度,LeetCode 上速度不够快。
我也是服了,算法看的是时间复杂度,你能确保自己的时间复杂度最优就行了。至于 LeetCode 所谓的运行速度,那个都是玄学,只要不是慢的离谱就没啥问题,根本不值得你从编译层面优化,不要舍本逐末……
labuladong 公众号的重点在于算法思想,你把框架思维了然于心套出解法,然后随你再魔改代码好吧,你高兴就好。
言归正传,下面就直接上四道 LeetCode 原题来套这个框架,其中第一道题会详细说明其原理,后面四道就直接闭眼睛秒杀了。
本文代码为 C++ 实现,不会用到什么编程方面的奇技淫巧,但是还是简单介绍一下一些用到的数据结构,以免有的读者因为语言的细节问题阻碍对算法思想的理解:
unordered_map 就是哈希表(字典),它的一个方法 count(key) 相当于 containsKey(key) 可以判断键 key 是否存在。
可以使用方括号访问键对应的值 map[key]。需要注意的是,如果该 key 不存在,C++ 会自动创建这个 key,并把 map[key] 赋值为 0。
1. 最小覆盖子串

题目不难理解,就是说要在 S(source) 中找到包含 T(target) 中全部字母的一个子串,顺序无所谓,但这个子串一定是所有可能子串中最短的。
如果我们使用暴力解法,代码大概是这样的:
for (int i = 0; i < s.size(); i++)
for (int j = i + 1; j < s.size(); j++)
if s[i:j] 包含 t 的所有字母:
更新答案
思路很直接吧,但是显然,这个算法的复杂度肯定大于 O ( N 2 ) O(N^2) O(N2) 了,不好。
滑动窗口算法的思路是这样:
- 我们在字符串
S中使用双指针中的左右指针技巧,初始化left = right = 0,把索引闭区间[left, right]称为一个「窗口」。 - 我们先不断地增加
right指针扩大窗口[left, right],直到窗口中的字符串符合要求(包含了T中的所有字符)。 - 此时,我们停止增加
right,转而不断增加left指针缩小窗口[left, right],直到窗口中的字符串不再符合要求(不包含T中的所有字符了)。同时,每次增加left,我们都要更新一轮结果。 - 重复第 2 和第 3 步,直到
right到达字符串S的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个 「可行解」 ,然后第 3 步在优化这个「可行解」,最终找到 最优解 。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
下面画图理解一下,needs 和 window相当于计数器,其中:
needs记录字符串T中的字符出现次数;window记录窗口中的相应字符的出现次数。
初始状态:

增加 right,直到窗口 [left, right] 包含了 T 中所有字符:
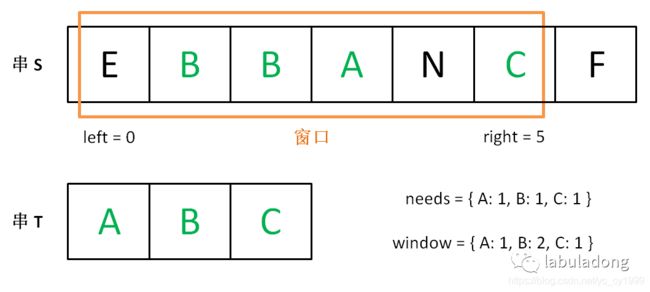
现在开始增加 left,缩小窗口 [left, right]。
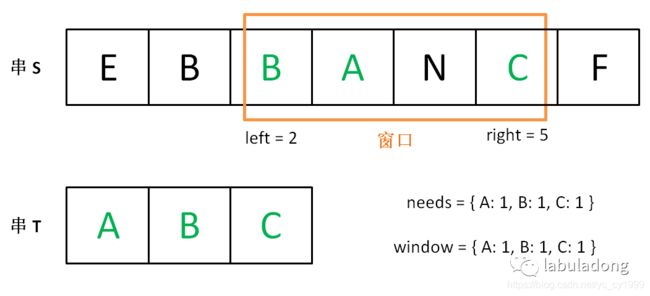
直到窗口中的字符串不再符合要求,left 不再继续移动。
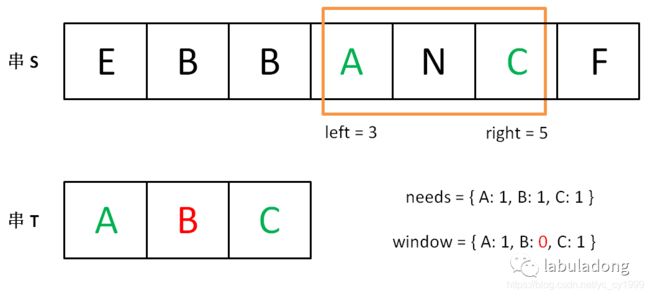
之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针超出了字符串 S的范围,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。至于如何具体到问题,如何得出此题的答案,都是编程问题,等会提供一套模板,理解一下就会了。
上述过程可以简单地写出如下伪码框架:
string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;
while(right < s.size()) {
window.add(s[right]);
right++;
// 如果符合要求,移动 left 缩小窗口
while (window 符合要求) {
// 如果这个窗口的子串更短,则更新 res
res = minLen(res, window);
window.remove(s[left]);
left++;
}
}
return res;
如果上述代码你也能够理解,那么你离解题更近了一步。现在就剩下一个比较棘手的问题:如何判断 window 即子串 s[left...right] 是否符合要求,是否包含 t 的所有字符呢?
可以用两个哈希表当作计数器解决。用一个哈希表 needs 记录字符串 t 中包含的字符及出现次数,用另一个哈希表 window 记录当前「窗口」中包含的字符及出现的次数,如果 window 包含所有 needs 中的键,且这些键对应的值都大于等于 needs 中的值,那么就可以知道当前「窗口」符合要求了,可以开始移动 left 指针了。
现在开始套模板,只需要思考以下四个问题:
1、当移动right扩大窗口,即加入字符时,应该更新哪些数据?
2、什么条件下,窗口应该暂停扩大,开始移动left缩小窗口?
3、当移动left缩小窗口,即移出字符时,应该更新哪些数据?
4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?(这个思考很重要)
如果一个字符进入窗口,应该增加window计数器;如果一个字符将移出窗口的时候,应该减少window计数器;当valid满足need时应该收缩窗口;应该在收缩窗口的时候更新最终结果。
现在将上面的框架继续细化:
string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;
// 相当于两个计数器
unordered_map<char, int> window;
unordered_map<char, int> needs;
for (char c : t) needs[c]++;
// 记录 window 中已经有多少字符符合要求了
int match = 0;
while (right < s.size()) {
char c1 = s[right];
if (needs.count(c1)) {
window[c1]++; // 加入 window
if (window[c1] == needs[c1])
// 字符 c1 的出现次数符合要求了
match++;
}
right++;
// window 中的字符串已符合 needs 的要求了
while (match == needs.size()) {
// 更新结果 res
res = minLen(res, window);
char c2 = s[left];
if (needs.count(c2)) {
window[c2]--; // 移出 window
if (window[c2] < needs[c2])
// 字符 c2 出现次数不再符合要求
match--;
}
left++;
}
}
return res;
上述代码已经具备完整的逻辑了,只有一处伪码,即更新 res 的地方,不过这个问题太好解决了,直接看解法吧!
string minWindow(string s, string t) {
// 记录最短子串的开始位置和长度
int start = 0, minLen = INT_MAX;
int left = 0, right = 0;
unordered_map<char, int> window;
unordered_map<char, int> needs;
for (char c : t) needs[c]++;
int match = 0;
while (right < s.size()) {
char c1 = s[right];
if (needs.count(c1)) {
window[c1]++;
if (window[c1] == needs[c1])
match++;
}
right++;
while (match == needs.size()) {
if (right - left< minLen) {
// 更新最小子串的位置和长度
start = left;
minLen = right - left;
}
char c2 = s[left];
if (needs.count(c2)) {
window[c2]--;
if (window[c2] < needs[c2])
match--;
}
left++;
}
}
return minLen == INT_MAX ?
"" : s.substr(start, minLen);
}
如果直接甩给你这么一大段代码,我想你的心态是爆炸的,但是通过之前的步步跟进,你是否能够理解这个算法的内在逻辑呢?你是否能清晰看出该算法的结构呢?
这个算法的时间复杂度是 O(M + N),M 和 N 分别是字符串 S 和 T 的长度。因为我们先用 for循环遍历了字符串 T 来初始化 needs,时间 O(N),之后的两个 while循环最多执行 2M 次,时间 O(M)。
读者也许认为嵌套的 while 循环复杂度应该是平方级,但是你这样想,while 执行的次数就是双指针 left 和 right 走的总路程,最多是 2M 嘛。
2. 字符串排列
LeetCode 567 题,Permutation in String,难度 Medium:

注意哦,输入的s1是可以包含重复字符的,所以这个题难度不小。
这种题目,是明显的滑动窗口算法,相当给你一个S和一个T,请问你S中是否存在一个子串,包含T中所有字符且不包含其他字符?
首先,先复制粘贴之前的算法框架代码,然后明确刚才提出的 4 个问题,即可写出这道题的答案:
// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 在这里判断是否找到了合法的子串
if (valid == need.size())
return true;
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
// 未找到符合条件的子串
return false;
}
对于这道题的解法代码,基本上和最小覆盖子串一模一样,只需要改变两个地方:
- 本题移动
left缩小窗口的时机是窗口大小大于t.size()时,因为排列嘛,显然长度应该是一样的。——什么条件下,窗口应该暂停扩大,开始移动left缩小窗口? - 当发现
valid == need.size()时,就说明窗口中就是一个合法的排列,所以立即返回true。——我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?
至于如何处理窗口的扩大和缩小,和最小覆盖子串完全相同。
3. 找所有字母异位词
这是 LeetCode 第 438 题,Find All Anagrams in a String,难度 Medium:

呵呵,这个所谓的字母异位词,不就是排列吗,搞个高端的说法就能糊弄人了吗?相当于,输入一个串S,一个串T,找到S中所有T的排列,返回它们的起始索引。
直接默写一下框架,明确刚才讲的 4 个问题,即可秒杀这道题:
vector<int> findAnagrams(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
vector<int> res; // 记录结果
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 当窗口符合条件时,把起始索引加入 res
if (valid == need.size())
res.push_back(left);
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
return res;
}
跟寻找字符串的排列一样,只是找到一个合法异位词(排列)之后将起始索引加入res即可。
4. 最长无重复子串
这是 LeetCode 第 3 题,Longest Substring Without Repeating Characters,难度 Medium:

这个题终于有了点新意,不是一套框架就出答案,不过反而更简单了,稍微改一改框架就行了:
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> window;
int left = 0, right = 0;
int res = 0; // 记录结果
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
window[c]++;
// 判断左侧窗口是否要收缩
while (window[c] > 1) {
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
window[d]--;
}
// 在这里更新答案
res = max(res, right - left);
}
return res;
}
这就是变简单了,连need和valid都不需要,而且更新窗口内数据也只需要简单的更新计数器window即可。
当window[c]值大于 1 时,说明窗口中存在重复字符,不符合条件,就该移动left缩小窗口了嘛。
唯一需要注意的是,在哪里更新结果res呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
这里和之前不一样,要在收缩窗口完成后更新res,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
5. 最后总结
建议背诵并默写这套框架,顺便背诵一下文章开头的那首诗。以后就再也不怕 子串、子数组问题 了。
6. 题型训练
- ⭐LeetCode 76. Minimum Window Substring
- LeetCode 567. Permutation in String
- LeetCode 438. Find All Anagrams in a String
- LeetCode 3. Longest Substring Without Repeating Characters
