leetcode：516. 最长回文子序列
题目来源
- leetcode
题目描述
题目解析
思路
暴力递归
class Solution {
int f(string &s, int L, int R){
if(L > R){
return 0;
}
if(L == R){
return 1;
}
if(s[L] == s[R]){
return f(s, L + 1, R - 1) + 2;
}
return std::max(f(s, L + 1, R), f(s, L, R - 1));
}
public:
int longestPalindromeSubseq(string s) {
return f(s, 0, (int)s.size() - 1);
}
};
会超时
暴力递归改动态规划
（1）准备一个表。考虑递归函数的变化参数的个数和范围
int longPSQ(string &s, int l, int r)
- L的取值范围：0~N-1
- R的取值范围：0~N-1
所以dp数组应该是一个二维数组，如下：
int dp[N][N]
（2）返回值，看主函数是怎么调用的
return longPSQ(s, 0, (int)s.size() - 1);
所以应该返回dp[0][N - 1]
（3）填表
- 由下面可以看出，只需要右上角
if(l > r){
return 0;
}
- 然后其对角线全部填1
if(l == r){
return 1;
}
- 普通情况，其依赖如下：
if(s[l] == s[r]){
return longPSQ(s, l + 1, r - 1) + 2;
}
return std::max(longPSQ(s, l + 1, r), longPSQ(s, l, r - 1));
- 所以应该从左到右，从下到上填
（4）综上，代码如下：
class Solution {
public:
int longestPalindromeSubseq(string s) {
int N = s.size();
if(N == 0){
return 0;
}
std::vector<std::vector<int>> dp(N, std::vector<int>(N, 0));
for (int i = 0; i < N; ++i) {
dp[i][i] = 1;
}
for (int i = N - 1; i >= 0; --i) {
for (int j = i + 1; j < N; ++j) {
if(s[i] == s[j]){
dp[i][j] = dp[i + 1][j - 1] + 2;
}else{
dp[i][j] = std::max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][N - 1];
}
};
思路：范围尝试模型（讨论开头和结尾）
暴力递归
定义一个递归函数：
int f(std::string str, int L, int R);
其含义为：在str[L…R]区间中，返回其最长回文子序列长度
主函数怎么调用它：
return f(s, 0, (int)s.size() - 1);
怎么实现呢？
（1）base case
- 如果L == R，那么返回1
- 如果L + 1 == R，也就是有两个字符时，那么：
- 如果str[L] == str[R]，那么返回2
- 否则返回1
（2）一般情况
- 最长回文子串既不以L开头，也不以R结尾，比如：a12321b -> 12321
- 最长回文子串以L开头，不以R结尾，比如：12a321b -> 12321
- 最长回文子串不以L开头，以R结尾， 比如：a123b321 -> 12321
- 最长回文子串以L开头，以R结尾，前提是str[L] == str[R]，比如：1ab23cd21 -> 12321
最终代码：
class Solution {
int f(string &str, int L, int R){
if(L == R){
return 1;
}
if(L == R - 1){
return str[L] == str[R] ? 2 : 1;
}
int p1 = f(str, L + 1, R - 1);
int p2 = f(str, L, R - 1);
int p3 = f(str, L + 1, R);
int p4 = str[L] != str[R] ? 0 : (2 + f(str, L + 1, R - 1));
return std::max(std::max(p1, p2), std::max(p3, p4));
}
public:
int longestPalindromeSubseq(string s) {
return f(s, 0, (int)s.size() - 1);
}
};
暴力递归改动态规划
（1）准备一个表。考虑递归函数的变化参数的个数和范围
int f(std::string str, int L, int R);
- L的取值范围：0~N-1
- R的取值范围：0~N-1
所以dp数组应该是一个二维数组，如下：
int dp[N][N]
（2）返回值，看主函数是怎么调用的
return f(s, 0, (int)s.size() - 1);
所以应该返回dp[0][N - 1]
（3）填表
综上，代码为：
class Solution {
public:
int longestPalindromeSubseq(string s) {
int N = s.size();
if(N <= 1){
return N;
}
int dp[N][N];
// std::vector> dp(N, std::vector(N, 0));
dp[N - 1][N - 1] = 1;
for (int i = 0; i < N - 1; ++i) {
dp[i][i] = 1;
dp[i][i + 1] = s[i] == s[i + 1] ? 2 : 1;
}
for (int i = N - 3; i >= 0; --i) {
for (int j = i + 2; j < N; ++j) {
dp[i][j] = std::max( dp[i][j - 1], dp[i + 1][j]);
if(s[i] == s[j]){
dp[i][j] = std::max(dp[i][j], 2 + dp[i - 1][j + 1]);
}
}
}
return dp[0][N - 1];
}
};
思路：样本对应模型（讨论结尾）
之前我们已经解决了leetcode：1143. 最长公共子序列 Longest Common Subsequence ，而现在我们有一个str1，需要得到它的最长回文子串。
思路：已经知道str1，现在得到str1的逆序str2，然后得到str1和str2的最长公共子序列，这个最长公共子序列就是str1的最长回文子串
class Solution {
int longestCommonSubsequence(string &str1, string &str2){
int N = str1.size(), M = str2.size();
std::vector<std::vector<int>> dp(N, std::vector<int>(M, 0));
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
for (int i = 1; i < N; i++) {
dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0];
}
for (int j = 1; j < M; j++) {
dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1];
}
for (int i = 1; i < N; i++) {
for (int j = 1; j < M; j++) {
dp[i][j] = std::max(dp[i - 1][j], dp[i][j - 1]);
if (str1[i] == str2[j]) {
dp[i][j] = std::max(dp[i][j], dp[i - 1][j - 1] + 1);
}
}
}
return dp[N - 1][M - 1];
}
public:
int longestPalindromeSubseq(string str) {
if(str.size() <= 1){
return str.size();
}
std::string rstr = str;
std::reverse(rstr.begin(), rstr.end());
return longestCommonSubsequence(str, rstr);
}
};
思路：动态规划
假设二维数组 dp[i][j] 记录子串 i…j 内的最长回文序列长度。
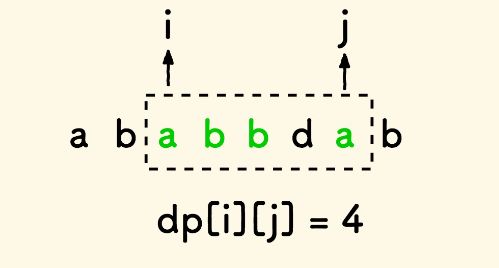
显然，任何一个子串的最长回文序列长度至少是 1， 即可初始化所有的 dp[i][j] = 1 。
考虑 dp 数组的递推关系。
如果子串的两边字符相等，那么去掉这俩字符后的子串的最长回文子序列长度比原来少了 2 。
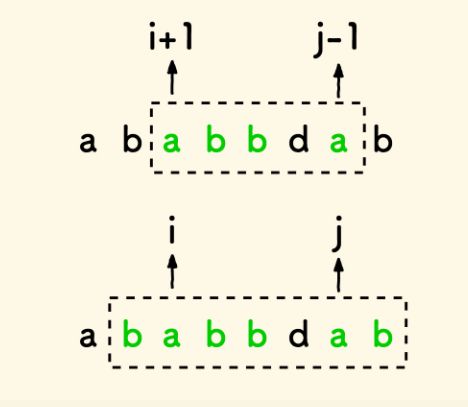
即当 s[i] == s[j] 时，dp[i][j] = dp[i+1][j-1] + 2 。
如果两边字符不相等，最长回文序列要么全落在去掉右边界字符后的左子串内，要么全落在去掉左边界字符后的右子串内 。
此时 dp[i][j] = max(dp[i+1][j], dp[i][j-1]) 。
上面的两种递推关系，对于子串起始位置的变量 i 的利用逻辑是：先知道 i+1 时候的情况，才能知道 i 时候的情况。 所以 应倒序迭代变量 i ，同样的道理， 应正序迭代变量 j 。
需要注意处理边界情况：
-
对于第一种递推情况，要考虑子串 i+1…j-1 的有效性，即 i+1 <= j-1 。
- 反之，子串 i…j 最多有两个字符，又考虑到其两头字符相等， 所以整个子串回文。最长回文子序列取其长度即可。
-
对于第二种递推情况，利用的两个左右子串必然是有效的。
- 因为此时子串 i…j 的两头字符不相等，所以必然其长度至少为 2 。
- 所以 i+1 <= j 和 i <= j-1 都成立。
- 不过，仍需要注意 i+1 和 j-1 的边界。
最后，要求的结果即 dp[0][n-1] ，其中 n 是字符串长度。
class Solution {
public:
int longestPalindromeSubseq(string s) {
if(s.empty()){
return 0;
}
int n = s.size();
// dp[i][j] 表示子串 i..j 内的最长回文序列长度
int dp[n][n];
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
// 初始化，至少为 1
dp[i][j] = 1;
if (s[i] == s[j]) {
// 第一种情况，两边字符相等 回文序列长度 += 2
// 注意子串i+1..j-1 的有效性
if (i + 1 <= j - 1)
dp[i][j] = dp[i + 1][j - 1] + 2;
else {
// 即 j-i <= 1 ，此时 i..j 至多有 2 个字符
// 两个字符相等时，自身回文，取其长度
dp[i][j] = j - i + 1;
}
} else {
// 第一种情况，两边字符不等 回文序列长度取左右之大
// 此时必然 j > i
// 所以，一定有 j >= i+1 或者 i-1 <= j，也就是子串一定有效
// 仍需要注意 i+1 和 j-1 的越界处理
if (i + 1 < n) dp[i][j] = max(dp[i][j], dp[i + 1][j]);
if (j - 1 >= 0) dp[i][j] = max(dp[i][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
};
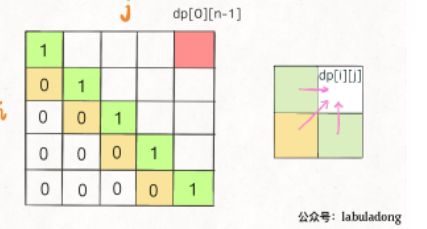
最后，用一个表格图示来更好地理解其规划过程。
上面的表格填表过程：
- 初始化所有方格写 1 。
- 自对角线右下角开始，自下而上、自左而右，按箭头方向根据递推关系填表。
- 如果 i 和 j 处字符相同，则填写 左下角数字 + 2 （图中绿色）。
- 否则，填写 左边和下边两个方格中较大的数字 （图中红色）。
动态规划：推导状态转移方程
（1）确定状态
-
最后一步：
- 最优策略产生最长的回文子串T，长度是M
- 情况一：回文串长度是1，即一个字母
- 情况二：回文串长度大于1，那么必须有
T[0] = T[M-1]
- 设T[0]为S[i]，T[M-1]是S[j]，则T剩下的部分T[1…M-2]仍然是一个回文串，而且是S[i+1…j-1]的最长回文串
- 最优策略产生最长的回文子串T，长度是M
-
子问题：
- 要求
S[i...j]的最长回文子串 - 如果S[i] = S[j]，需要知道S[i+1…j-1]的最长回文子串
- 如果S[i] !=S[j]，答案是S[i+1…j]的最长回文子串或者S[i…j-1]的最长回文子串
- 要求
-
状态：
- dp[i][j]表示s[i…j]的最长回文子串的长度
（2）转移方程
-
要求
dp[i...j]的最长回文子串，假设我们已经知道dp[i+1][j-1]的最长回文子序列，能不能算出dp[i][j]的值呢？
- 可以，这取决于S[i]和S[j]的字符
- 如果它们相等，那么它们加上s[i+1…j-1] 中的最长回文子序列就是 s[i…j] 的最长回文子序列：
- 如果它俩不相等，说明它俩不可能同时出现在 s[i…j] 的最长回文子序列中，那么把它俩分别加入 s[i+1…j-1] 中，看看哪个子串产生的回文子序列更长即可：
if (s[i] == s[j])
// 它俩一定在最长回文子序列中
dp[i][j] = dp[i + 1][j - 1] + 2;
else
// s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
（3）初始情况和边界情况
- 初始条件：
- 如果只有一个字符，显然最长回文子序列长度是 1，也就是 f[0][0] = f[1][1] = … = f[N-1][N-1] = 1，即：dp[i][j] = 1 (i == j)。
- 如果s[i] == s[i+1]，那么dp[i][i+1] = 2
- 如果s[i] ！= s[i+1]，那么dp[i][i+1] = 1
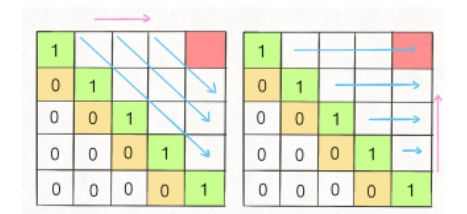
（4）遍历顺序
- 因为i肯定小于j，所以对于那些i > j的位置，根本不存在什么子序列，应该初始化为0
- 另外，看看刚才写的状态转移方程，想求 dp[i][j] 需要知道 dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1] 这三个位置；再看看我们确定的 base case，填入 dp 数组之后是这样：
- 为了保证每次计算 dp[i][j]，左下右方向的位置已经被计算出来，只能斜着遍历或者反着遍历：
- 区间型动态规划，可以按照长度j - i从小到大的顺序去计算（斜着算）
- 长度1： dp[0][0]、dp[1][1]…dp[N-1][N-1]
- 长度2：dp[0][1]、dp[1][2]…dp[N-2][N-1]
- …
- 长度N：dp[0][N-1]
- 答案是dp[0][N-1]
class Solution {
public:
int longestPalindromeSubseq(string s) {
int m = s.length();
if(m == 0){
return 0;
}
std::vector<std::vector<int>> dp(m,std::vector<int>(m));
// init
//length 1
for (int i = 0; i < m; ++i) {
dp[i][i] = 1;
}
//length 2
for (int i = 0; i < m - 1; ++i) {
if(s[i] == s[i + 1]){
dp[i][i + 1] = 2;
}else{
dp[i][i + 1] = 1;
}
}
for (int len = 0; len <= m; ++len) {
for (int i = 0; i + len <= m ; ++i) {
int j = i + len - 1;
char front = s[i], end = s[j];
if(s[i] == s[j]){
dp[i][j] = dp[i + 1][j - 1] + 2;
}else{
dp[i][j] = std::max(dp[i][j - 1], dp[i + 1][j]);
}
}
}
return dp[0][m - 1];
}
};
小结
这是一道经典的区间dp题。之所以可以使用区间dp进行求解，是因为在给定一个回文串的基础上，如果在回文串的边缘分别添加两个新的字符，可以通过判断两字符是否相等来得知新串是否回文
也就是说，使用小区间的回文状态可以推导出大区间的回文状态值。
从图论上来看，任何一个长度为len的回文串，必然由[长度为len-1]或者[长度为len-2]的回文串转移而来
通常区间len问题都是：
- 从小到达枚举区间大小len
- 枚举区间左端点l，同时根据区间大小len和左端点计算出右端点r = l + len - 1
- 通过状态转移方程求dp[l][r]的值
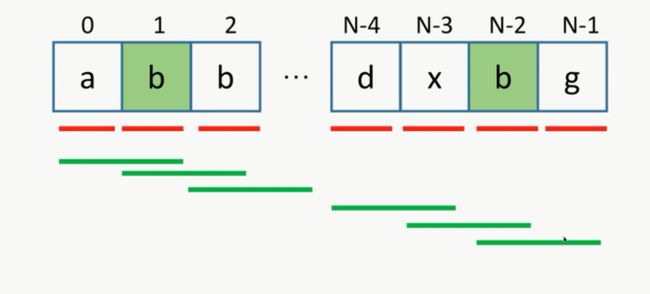
扩展： 输出所有最长回文子序列
- 填表过程
- 最长回文子序列问题（两种方法）