数字信号处理第六次试验:数字信号处理在双音多频拨号系统中的应用
数字信号处理第六次试验:数字信号处理在双音多频拨号系统中的应用
- 前言
- 一、实验目的
- 二、实验原理和方法
-
- 1.关于双音多频拨号系统
- 2.电话中的双音多频(DTMF)信号的产生与检测
- 3.检测DTMF信号的DFT参数选择
- 4.DTMF信号的产生与识别仿真实验
- 三、实验内容
- 四、实验报告
- 五、实验结果
- 六、思考题
前言
为了帮助同学们完成痛苦的实验课程设计,本作者将其作出的实验结果及代码贴至CSDN中,供同学们学习参考。如有不足或描述不完善之处,敬请各位指出,欢迎各位的斧正!
一、实验目的
通过对双音多频拨号系统的分析与仿真实验,了解双音多频信号的产生、检测,包括对双音多频信号进行DFT时的参数选择等,使学生初步了解数字信号处理在实际中的使用方法和重要性。
二、实验原理和方法
1.关于双音多频拨号系统
双音多频(Dual Tone Multi Frequency, DTMF)信号是音频电话中的拨号信号,由美国AT&T贝尔公司实验室研制,并用于电话网络中。这种信号制式具有很高的拨号速度,且容易自动监测识别,很快就代替了原有的用脉冲计数方式的拨号制式。这种双音多频信号制式不仅用在电话网络中,还可以用于传输十进制数据的其它通信系统中,也可用于电子邮件和银行系统中。在这些系统中,用户可以用电话发送DTMF信号,选择语音菜单进行操作。
DTMF信号系统是一个典型的小型信号处理系统。它以数字方法产生模拟信号并进行传输,其中还用到了D/A变换器;在接收端用A/D变换器将其转换成数字信号,并进行数字信号处理与识别。为了系统地检测速度并降低成本,还开发了一种特殊的DFT算法,成为戈泽尔(Goertzel)算法。这种算法既可以用硬件(专用芯片)实现,也可以用软件实现。下面首先介绍双音多频信号的产生方法和检测方法,包括戈泽尔算法,最后进行模拟实验。下面先介绍电话中的DTMF信号的组成。
在电话中,数字0~9中的每一个都用两个不同的单音频传输,所用的8个频率分成高频带和低频带两组,低频带有四个频率:679Hz、770Hz、852Hz和941Hz;高频带也有四个频率:1209Hz、1336Hz、1477Hz和1633Hz。每一个数字均由高、低频带中的各一个频率构成,例如1用697Hz和1209Hz两个频率构成,信号用 s i n ( 2 π f 1 t ) + s i n ( 2 π f 2 t ) sin(2\pi f_1 t)+sin(2\pi f_2 t) sin(2πf1t)+sin(2πf2t)表示,其中 f 1 = 679 H z f_1 =679Hz f1=679Hz, f 2 = 1209 H z f_2 =1209Hz f2=1209Hz。这样8个频率形成16种不同的双频信号。具体号码以及符号对应的频率如表8.6.1所示。表中最后一列在电话中暂时未用
| 行\列 | 1209Hz | 1336Hz | 1477Hz | 633Hz |
|---|---|---|---|---|
| 697Hz | 1 | 2 | 3 | A |
| 770Hz | 4 | 5 | 6 | B |
| 852Hz | 7 | 8 | 9 | C |
| 942Hz | * | 0 | # | D |
DTMF信号在电话中有两种作用,一个是拨号信号去控制交换机接通被叫的用户电话机,另一个作用是控制电话机的各种动作,如播放留言、语音信箱等。
2.电话中的双音多频(DTMF)信号的产生与检测
(1)双音多频信号的产生。假设时间连续的DTMF信号用 x ( t ) = s i n ( 2 π f 1 t ) + s i n ( 2 π f 2 t ) x(t)=sin(2\pi f_1 t)+sin(2\pi f_2 t) x(t)=sin(2πf1t)+sin(2πf2t)表示,式中 f 1 f_1 f1和 f 2 f_2 f2是按照表8.6.1选择的两个频率, f 1 f_1 f1代表低频带中的一个频率, f 2 f_2 f2代表高频带中的一个频率。显然,采用数字方法产生DTMF信号,优点是方便而且体积小。下面介绍采用数字方法产生DTM信号。规定用8kHz对DTMF信号进行采样,采样后得到时域离散信号为
x ( n ) = s i n 2 π f 1 n 8000 + s i n 2 π f 2 n 8000 x(n)=sin\frac{2\pi f_1 n}{8000}+sin\frac{2\pi f_2 n}{8000} x(n)=sin80002πf1n+sin80002πf2n
形成上面序列的方法有两种,即计算法和查表法。用计算法求正弦波的序列值容易,但实际中要占用一些计算时间,影响运行速度。查表法是预先将正弦波的各序列值计算出来,寄存在存储器中,运行时只要按顺序和一定的速度取出便可,这种方法要占用一定的存储空间,但是速度快。
因为采样频率是8000Hz,因此要求每125ms输出一个样本,得到的序列再送到D/A变换器和平滑滤波器,输出便是连续时间的DTMF信号。DTMF信号通过电话线路送到交换机。
(2)双音多频信号的检测。在接收端,要对收到的双音多频信号进行检测,检测两个正弦波的频率是多少,以判断所对应的十进制数字或者符号。显然,这里仍然要用数字方法进行检测,因此要将收到的时间连续DTMF信号经过A/D变换,变成数字信号进行检测。检测的方法有两种,一种是用一组滤波器提取所关心的频率,根据有输出信号的两个滤波器判断相应的数字或符号。另一种是用DFT(FFT)对双音多频信号进行频谱分析,由信号的幅度谱,判断信号的两个频率,最后确定相应的数字或符号。当检测的音频数目较少时,用滤波器组实现更合适。FFT是DFT的快速算法,但当DFT的变换区间较小时,FFT快速算法的效果并不明显,而且还要占用很多内存,因此不如直接用DFT合适。下面介绍Goertzel算法,这种算法的实质是直接计算DFT的一种线性滤波方法。这里略去Goertzel算法的介绍(请参考文献[19]),可以直接调用MATLAB信号处理工具箱中戈泽尔算法的函数Goertzel,计算N点DFT的几个感兴趣的频点的值。
3.检测DTMF信号的DFT参数选择
用DFT检测模拟DTMF信号所含有的两个音频频率,是一个用DFT对模拟信号进行频谱分析的问题。根据第3章用DFT对模拟信号进行谱分析的理论,确定三个参数:①采样频率 F s F_s Fs;② DFT的变换点数N;③需要对信号的观察时间的长度 T p T_p Tp。这三个参数不能随意选取,要根据对信号频谱分析的要求进行确定。这里对信号频谱分析也有三个要求:①频谱分析的分辨率;②频谱分析的频率范围;③检测频率的准确性。
(1)频谱分析的分辨率。观察要检测的8个频率,相邻间隔最小的是第一和第二个频率,间隔是73Hz,要求DFT最少能够分辨相隔73Hz的两个频率,即要求 F m i n = 73 H z F_{min}=73Hz Fmin=73Hz。DFT的分辨率与对信号的观察时间 T p T_p Tp有关, T p m i n = 1 / F = 1 / 73 = 13.7 m s T_{pmin}=1/F=1/73=13.7 ms Tpmin=1/F=1/73=13.7ms。考虑到可靠性,留有富裕量,要求按键的时间大于40 ms。
(2)频谱分析的频率范围。要检测的信号频率范围是697 ~ 1633Hz,但考虑到存在语音干扰,除了检测这8个频率外,还要检测它们的二次倍频的幅度大小,波形正常且干扰小的正弦波的二次倍频是很小的,如果发现二次谐波很大,则不能确定这是DTMF信号。这样频谱分析的频率范围为697 ~ 3266Hz。按照采样定理,最高频率不能超过折叠频率,即0.5 F s ≥ 3622 H z F_s\geq3622 Hz Fs≥3622Hz,由此要求最小的采样频率应为7.24 kHz。因为数字电话总系统已经规定 F s = 8 k H z F_s=8 kHz Fs=8kHz,因此对频谱分析范围的要求是一定满足的。按照 T p m i n = 13.7 m s T_{pmin}=13.7ms Tpmin=13.7ms, F s = 8 k H z F_s=8kHz Fs=8kHz,算出对信号最少的采样点数为 N m i n = T p m i n ⋅ F s ≈ 110 N_{min}=T_{pmin}·F_s\approx110 Nmin=Tpmin⋅Fs≈110。
(3)检测频率的准确性。这是一个用DFT检测正弦波频率是否准确的问题。序列的.N点DFT是对序列频谱函数在0~ 2 π 2\pi 2π区间的N点等间隔采样。如果是一个周期序列,截取周期序列的整数倍周期,进行DFT,其采样点刚好在周期信号的频率上,DFT的幅度最大处就是信号的准确频率。分析这些DTMF信号,发现不可能经过采样而得到周期序列,因此存在检测频率的准确性问题。
DFT的频率采样点频率为 ω k = 2 π k ( k = 0 , 1 , 2 , … , N − 1 ) ω_k=2\pi k(k=0,1,2,…,N-1) ωk=2πk(k=0,1,2,…,N−1),相应的模拟域采样点频率为 f k = F s k / N ( k = 0 , 1 , 2 , … , N − 1 ) f_k=F_sk/N(k=0,1,2,…,N-1) fk=Fsk/N(k=0,1,2,…,N−1),希望选择一个合适的N,使用该公式算出的 f k f_k fk能接近要检测的频率,或者用8个频率中的任一个频率 f k ′ f_k' fk′代入公式 f k ′ = F s k / N f_k'=F_sk/N fk′=Fsk/N中时,得到的k值最接近整数值,这样虽然用幅度最大点检测的频率有误差,但可以准确判断所对应的DTMF频率,即可以准确判断所对应的数字或符号。经过分析研究,认为N=205是最好的。按照 F s = 8 k H z F_s=8 kHz Fs=8kHz,N=205,算出的8个频率及其二次谐波对应的k值,以及k取整数时的频率误差见表8.6.2。
| 8个基频/Hz | 最近的整数k值 | DFT的k值 | 绝对误差 | 二次谐波/Hz | 对应的k值 | 最近的整数k值 | 绝对误差 |
|---|---|---|---|---|---|---|---|
| 697 | 17.861 | 18 | 0.139 | 1394 | 35.024 | 35 | 0.021 |
| 770 | 19.531 | 20 | 0.269 | 1540 | 38.692 | 39 | 0.308 |
| 852 | 21.833 | 22 | 0.167 | 1704 | 42.813 | 43 | 0.187 |
| 941 | 24.113 | 24 | 0.113 | 1882 | 47.285 | 47 | 0.285 |
| 1209 | 30.981 | 31 | 0.019 | 2418 | 60.752 | 61 | 0.248 |
| 1336 | 34.235 | 34 | 0.235 | 2672 | 67.134 | 67 | 0.134 |
| 1477 | 37.848 | 38 | 0.152 | 2954 | 74.219 | 74 | 0.219 |
| 1633 | 41.846 | 42 | 0.154 | 3266 | 82.058 | 82 | 0.058 |
通过以上分析,确定 F s = 8 k H z F_s=8 kHz Fs=8kHz,N=205, T p ≥ 40 m s T_p\geq40 ms Tp≥40ms。
4.DTMF信号的产生与识别仿真实验
下面先介绍MATLAB工具箱函数goertzel,然后介绍DTMF信号的产生与识别仿实验程序。Goerztel函数的调用格式为
X g k = g o e r t z e l ( x n , K ) Xgk=goertzel(xn,K) Xgk=goertzel(xn,K)
xn是被变换的时域序列,用于DTMF信号检测时,xn就是DTMF信号的205个采样值。K是要求计算的DFT[xn]的频点序号向量,用N表示xn的长度,则要求 1 ≤ ∣ K ∣ ≤ N 1\leq |K| \leq N 1≤∣K∣≤N,由表8.6.2可知,如果只计算DTMF信号8个基频时,
K = [ 18 , 20 , 22 , 24 , 31 , 34 , 38 , 42 ] K=[18,20,22,24,31,34,38,42] K=[18,20,22,24,31,34,38,42]
如果同时计算个基频及其二次谐波时,
K = [ 18 , 20 , 22 , 24 , 31 , 34 , 35 , 38 , 39 , 42 , 43 , 47 , 61 , 67 , 74 , 82 ] K=[18,20,22,24,31,34,35,38,39,42,43,47,61,67,74,82] K=[18,20,22,24,31,34,35,38,39,42,43,47,61,67,74,82]
Xgk是变换结果向量,其中存放的是由K指定的频率点的DFT[x(n)]的值。设X(k)=DFT[x(n)],则
X ( K ( i ) ) = X g k ( i ) i = 1 , 2 , … , l e n g t h ( K ) X(K(i))=Xgk(i) i=1,2,…,length(K) X(K(i))=Xgk(i)i=1,2,…,length(K)
DTMF信号的产生与识别仿真实验在MATLAB环境下进行,编写仿真程序,运行程序,送入6位电话号码,程序自动产生每一位号码数字相应的DTMF信号,并送出双声音,再用DFT进行谱分析,显示每一位号码数字的DTMF信号的DFT幅度谱,按照幅度谱的最大值确定对应的频率,再按照频率确定每一位对应的号码数字,最后输出6位电话号码。
本实验程序较复杂,所以将仿真程序提供给读者,只要求读者读懂程序,直接运行程序仿真。程序名为exp6.m。程序分四段:第一段(第2 ~ 7行)设置参数,并读入6位电话号码;第二段(第9 ~ 20行)根据键入的6位电话号码产生时域离散DTMF信号,并连续发出6位号码对应的双音频声音;第三段(第22 ~ 25行)对时域离散DTMF信号进行频率检测,画出幅度谱;第四段(第26 ~ 33行)根据幅度谱的两个峰值,分别查找并确定输入的6位电话号码。根据程序中的注释很容易分析编程思想和处理算法。程序清单如下:
%实验六程序 exp6.m
%DTMF双频拨号信号的生成和检测程序
clear;clc;
tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; %DTMF信号代表的16个数
N=205;K=[18,20,22,24,31,34,38,42];
f1=[697,770,852,941];
f2=[1209,1336,1477,1633];
TN=input('键入6位电话号码=');
TNr=0;
for l=1:6
d=fix(TN/10^(6-l));
TN=TN-d*10^(6-l);
for p=1:4
for q=1:4
if tm(p,q)==abs(d);break,end %检测码相符的列号q
end
if tm(p,q)==abs(d);break,end %检测码相符的行号p
end
n=0:1023;
x=sin(2*pi*n*f1(p)/8000)+sin(2*pi*n*f2(q)/8000);
sound(x,8000);
pause(0.1)
%接收检测端的程序
X=goertzel(x(1:205),K+1);
val=abs(X);
subplot(3,2,l);
stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|')
axis([10 50 0 120])
limit=80;
for s=5:8
if val(s)>limit,break,end
end
for r=1:4
if val(r)>limit,break,end
end
TNr=TNr+tm(r,s-4)*10^(6-l);
end
disp('接收端检测到的号码为:')
disp(TNr)
三、实验内容
(1)运行仿真程序exp6.m,任意送入6位电话号码,打印出相应的幅度谱。观察程序运行结果,对照表8.6.1和表8.6.2,判断程序谱分析的正确性。
(2)分析该仿真程序,将产生、检测和识别6位电话号码的程序改为能产生、检测和识别8位电话号码的程序,并运行一次,打印出相应的幅度谱和8位电话号码。
四、实验报告
(1)打印6位和8位电话号码DTMF信号的幅度谱。
(2)简述DTMF信号的参数:采样频率、DFT 的变换点数以及观测时间的确定原则。
五、实验结果
六位电话号码:
%实验六程序 exp6.m
%DTMF双频拨号信号的生成和检测程序
clear;clc;
tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; %DTMF信号代表的16个数
N=205;K=[18,20,22,24,31,34,38,42];
f1=[697,770,852,941];
f2=[1209,1336,1477,1633];
TN=input('键入6位电话号码=');
TNr=0;
for l=1:6
d=fix(TN/10^(6-l));
TN=TN-d*10^(6-l);
for p=1:4
for q=1:4
if tm(p,q)==abs(d);break,end %检测码相符的列号q
end
if tm(p,q)==abs(d);break,end %检测码相符的行号p
end
n=0:1023;
x=sin(2*pi*n*f1(p)/8000)+sin(2*pi*n*f2(q)/8000);
sound(x,8000);
pause(0.1)
%接收检测端的程序
X=goertzel(x(1:205),K+1);
val=abs(X);
subplot(3,2,l);
stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|')
axis([10 50 0 120])
limit=80;
for s=5:8
if val(s)>limit,break,end
end
for r=1:4
if val(r)>limit,break,end
end
TNr=TNr+tm(r,s-4)*10^(6-l);
end
disp('接收端检测到的号码为:')
disp(TNr)
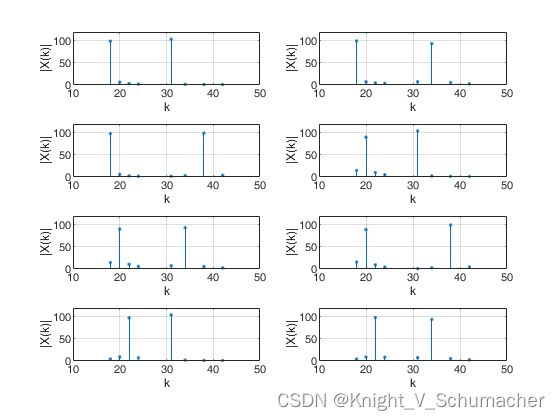
八位电话号码:
%DTMF双频拨号信号的生成和检测程序
clear;clc;
tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; %DTMF信号代表的16个数
N=205;K=[18,20,22,24,31,34,38,42];
f1=[697,770,852,941];
f2=[1209,1336,1477,1633];
TN=input('键入8位电话号码=');
TNr=0;
for l=1:8
d=fix(TN/10^(8-l));
TN=TN-d*10^(8-l);
for p=1:4
for q=1:4
if tm(p,q)==abs(d);break,end %检测码相符的列号q
end
if tm(p,q)==abs(d);break,end %检测码相符的行号p
end
n=0:1023;
x=sin(2*pi*n*f1(p)/8000)+sin(2*pi*n*f2(q)/8000);
sound(x,8000);
pause(0.1)
%接收检测端的程序
X=goertzel(x(1:205),K+1);
val=abs(X);
subplot(4,2,l);
stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|')
axis([10 50 0 120])
limit=80;
for s=5:8
if val(s)>limit,break,end
end
for r=1:4
if val(r)>limit,break,end
end
TNr=TNr+tm(r,s-4)*10^(8-l);
end
disp('接收端检测到的号码为:')
disp(TNr)
六、思考题
(2)简述DTMF信号的参数:采样频率、DFT 的变换点数以及观测时间的确定原则。
答:(1)频谱分析的分辨率。观察要检测的8个频率,相邻间隔最小的是第一和第二个频率,间隔是73Hz,要求DFT最少能够分辨相隔73Hz的两个频率,即要求 F m i n = 73 H z F_{min}=73Hz Fmin=73Hz。DFT的分辨率与对信号的观察时间 T p T_p Tp有关, T p m i n = 1 / F = 1 / 73 = 13.7 m s T_{pmin}=1/F=1/73=13.7 ms Tpmin=1/F=1/73=13.7ms。考虑到可靠性,留有富裕量,要求按键的时间大于40 ms。
(2)频谱分析的频率范围。要检测的信号频率范围是697 ~ 1633Hz,但考虑到存在语音干扰,除了检测这8个频率外,还要检测它们的二次倍频的幅度大小,波形正常且干扰小的正弦波的二次倍频是很小的,如果发现二次谐波很大,则不能确定这是DTMF信号。这样频谱分析的频率范围为697 ~ 3266Hz。按照采样定理,最高频率不能超过折叠频率,即0.5 F s ≥ 3622 H z F_s\geq3622 Hz Fs≥3622Hz,由此要求最小的采样频率应为7.24 kHz。因为数字电话总系统已经规定 F s = 8 k H z F_s=8 kHz Fs=8kHz,因此对频谱分析范围的要求是一定满足的。按照 T p m i n = 13.7 m s T_{pmin}=13.7ms Tpmin=13.7ms, F s = 8 k H z F_s=8kHz Fs=8kHz,算出对信号最少的采样点数为 N m i n = T p m i n ⋅ F s ≈ 110 N_{min}=T_{pmin}·F_s\approx110 Nmin=Tpmin⋅Fs≈110。
(3)检测频率的准确性。这是一个用DFT检测正弦波频率是否准确的问题。序列的.N点DFT是对序列频谱函数在0~ 2 π 2\pi 2π区间的N点等间隔采样。如果是一个周期序列,截取周期序列的整数倍周期,进行DFT,其采样点刚好在周期信号的频率上,DFT的幅度最大处就是信号的准确频率。分析这些DTMF信号,发现不可能经过采样而得到周期序列,因此存在检测频率的准确性问题。
DFT的频率采样点频率为 ω k = 2 π k ( k = 0 , 1 , 2 , … , N − 1 ) ω_k=2\pi k(k=0,1,2,…,N-1) ωk=2πk(k=0,1,2,…,N−1),相应的模拟域采样点频率为 f k = F s k / N ( k = 0 , 1 , 2 , … , N − 1 ) f_k=F_sk/N(k=0,1,2,…,N-1) fk=Fsk/N(k=0,1,2,…,N−1),希望选择一个合适的N,使用该公式算出的 f k f_k fk能接近要检测的频率,或者用8个频率中的任一个频率 f k ′ f_k' fk′代入公式 f k ′ = F s k / N f_k'=F_sk/N fk′=Fsk/N中时,得到的k值最接近整数值,这样虽然用幅度最大点检测的频率有误差,但可以准确判断所对应的DTMF频率,即可以准确判断所对应的数字或符号。经过分析研究,认为N=205是最好的。