《数据结构与算法》 第二章 线性表

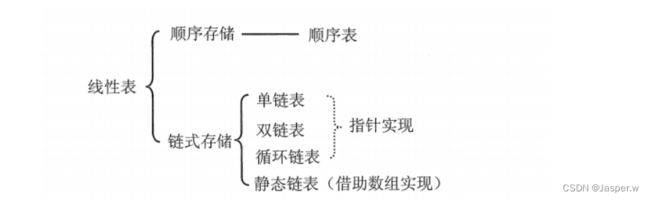
知识框架

一、线性表定义

线性表的数据集合为{a1,a2,…,an}，假设每个元素的类型均为DataType。其中，除第一个元素a1外，每一个元素有且只有一个直接前驱元素，除了最后一个元素an外，每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
在较复杂的线性表中，一个数据元素可以由若干个数据项组成。在这种情况下，常把数据元素称为记录，含有大量记录的线性表又称为文件。

二、顺序表（线性表的顺序存储结构）

1、顺序表的基本概念

概念：用一组地址连续的存储单元依次存储线性表的数据元素，这种存储结构的线性表称为顺序表。

特点：逻辑上相邻的数据元素，物理次序也是相邻的。

只要确定好了存储线性表的起始位置，线性表中任一数据元素都可以随机存取，所以线性表的顺序存储结构是一种随机存取的储存结构，因为高级语言中的数组类型也是有随机存取的特性，所以通常我们都使用数组来描述数据结构中的顺序储存结构，用动态分配的一维数组表示线性表。

2、代码实现

//头文件
#include
#include

#define MAXSIZE 20  //线性表存储空间的初始分配量
#define OK 1    //成功标识
#define ERROR 0 //失败标识

typedef int Status;	//Status是函数的类型，其值是函数结果状态代码，如OK等

typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int
//顺序表数据结构
typedef struct
{
    ElemType *elem;
    int length;
}SqList;





//构造一个空的线性表L
Status InitList(SqList* L){
    L -> elem = (ElemType *)malloc(MAXSIZE*sizeof(ElemType));
    if(!L -> elem){
        return ERROR;
    }
    L -> length = 0;
    return OK;
}




/*
插入操作
初始条件：顺序表L已存在
操作结果：在L中的第i个位置之前插入新的数据元素e，L的长度加1
*/
Status ListInsert(SqList *L, int i, ElemType e){
    int k;
    if (L->length == MAXSIZE){  //线性表已满
        return ERROR;
    }   
    if (i < 1 || i > L->length+1){ //当i不在范围内时
        return ERROR;
    }
    if (i <= L->length){  //若插入位置不在表尾
        for(k = L->length-1;k >= i-1;k--){
            L->elem[k+1] = L->elem[k];
        }
    }   
    L->elem[i-1] = e;   //将新元素插入
    L->length++;    //长度加1
    return OK;
}




/*
删除操作
初始条件：顺序表L已存在
操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1
*/
Status ListDelete(SqList *L, int i, ElemType *e){
    int k;
    if(L->length == 0){   //线性表为空
        return ERROR;
    }
    if(i < 1 || i > L->length){ //删除位置不正确
        return ERROR;
    }
    *e = L -> elem[i-1];
    if(i < L->length){  //如果删除位置不在最后位置
        for(k = i;k < L->length;k++){
            L->elem[k-1] = L->elem[k];
        }
    }
    L->length--;    //长度减1
    return OK;
}



/*
获取元素操作
初始条件：顺序表L已存在
操作结果：用e返回L中第i个数据元素的值
*/
Status GetElem(SqList L, int i, ElemType *e){
    if(L.length == 0 || i<1 || i>L.length){
        return ERROR;
    }
    *e = L.elem[i-1];
    return OK;
}



/*打印线性表中的所有元素*/
void OutPut(SqList L){
    printf("当前顺序表的长度:%d\n", L.length);
    for(int i = 0; i < L.length; i++){
        printf("%d ",L.elem[i]);
    }
    printf("\n");
}




int main()
{
    SqList L;
    printf("------构造一个空的线性表L------\n");
    InitList(&L);
    OutPut(L);  //打印结果
    printf("------测试插入10个数------\n");
    for(int i = 1;i <= 10; i++){
        ListInsert(&L,i,i);
    }
    OutPut(L);  //打印结果
    printf("------在第三位之前插入0------\n");
    ListInsert(&L,3,0);
    OutPut(L);  //打印结果
    printf("------删除第6位的数据------\n");
    ElemType e;
    ListDelete(&L,6,&e);
    printf("删除的数据为：%d\n", e);
    OutPut(L);  //打印结果
    printf("------获取元素操作------\n");
    GetElem(L,5,&e);
    printf("得到第5个元素：%d", e);
}

小结

①、顺序表时间复杂度

从以上代码可以很明显的看出，线性表的顺序存储结果在读、存数据是的时间复杂度是O(1)，插入、删除操作的时间复杂度是O(n)。

②、顺序表的优缺点

优点：无须为表中元素之间的逻辑关系而增加额外的存储空间；可以快速的存取表中任一位置的元素。
缺点：插入和删除操作需要移动大量元素；当线性表长度较大时，难以确定存储空间的容量；造成存储空间的“碎片”。

---

三、单链表

1、单链表的基本概念

  在链式结构中，除了要存储数据元素的信息外，还要存储它的后继元素的存储地址。因此，为了表示每个数据元素ai与其直接后继元素ai+1之间的逻辑关系，对数据ai来说，除了存储其本身的信息之外，还需要存储一个指示其直接后继的信息（即直接后继的存储位置）。我们吧把存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称做指针或链。这两部分信息组成数据元素ai的存储映像，称为结点（Node）。
n个结点（ai的存储映像）链结成一个链表，即为线性表（a1, a2, …, an）的链式存储结构，因为此链表的每个结点中只包含一个指针域，所以叫做单链表。

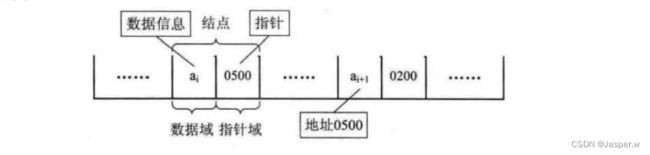
把链表中第一个结点的存储位置叫做头指针。

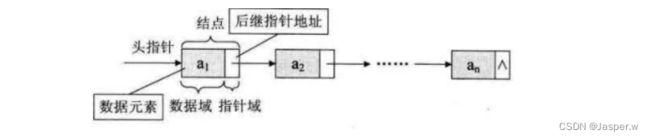
时为了方便对链表进行操作，会在单链表的第一个结点前附设一个节点，称为头结点，此时头指针指向的结点就是头结点。

空链表，头结点的直接后继为空。
假设p是指向线性表第i个数据元素的指针，p->data表示第i个位置的数据域，p->next表示第i+1个位置的指针域，则第p+i个数据元素可表示为：

2、代码实现

#define OK 1    //正确标识
#define ERROR 0 //失败标识

typedef int Status; //Status是函数的类型，其值是函数结果状态代码，如OK等

typedef int ElemType;   //ElemType的类型根据实际情况而定，这里假定为int

/*线性表的单链表存储结构*/
//构造结点
typedef struct Node
{
    ElemType data;
    struct Node *next;
} Node;

//构造LinkList
typedef struct {
    int lenght;
    Node *next;
}*LinkList;




/*构造一个带头结点的单链表*/
Status InitList(LinkList *L){
    //生成一个空的LinkList和一个新结点
    LinkList p = (LinkList)malloc(sizeof(LinkList));
    Node *q = (Node *)malloc(sizeof(Node)); //头结点
    q->next = NULL; //头结点的后继指向null
    p->next = q;    //头指针指向头结点
    p->lenght = 0;  //初始长度为0
    (*L) = p;
    return OK;
}




/**
 * 单链表插入操作
 * 初始条件：线性表L已存在
 * 操作结果：在L中第pos个位置之前插入新的数据元素e，L的长度增加1
*/
Status ListInsert(LinkList *L, ElemType elem, int pos){
    if(pos<1 || pos > (*L)->lenght+1){
        return ERROR;
    }
    //寻找第pos个结点
    Node *p = (*L)->next; //头结点
    for(int i=1; i<pos; i++){
        p = p->next;
    }
    //生成一个新结点
    Node *q = (Node *) malloc(sizeof(Node));
    q->data = elem;
    q->next = p->next;  //将p的后继赋值给q的后继
    p->next = q;    //将q赋值给p的后继
    (*L)->lenght += 1;  //链表长度加1
    return OK;
}




/**
 * 单链表删除操作
 * 初始条件：线性表L已存在
 * 操作结果：删除L的第pos个数据元素，并用e返回其值，L的长度减1
*/
Status ListDelete(LinkList *L, ElemType *elem, int pos){
    if(pos < 1 || pos>(*L)->lenght){
        return ERROR;
    }
    //寻找到第pos个结点
    Node *p = (*L)->next, *q;
    for(int i=1; i<pos; i++){
        p=p->next;
    }
    q = p->next;    //要删除的结点
    p->next = q->next;
    free(q);
    (*L) -> lenght -= 1;
    return OK;
}




/**
 * 清空单链表
*/
Status Clear(LinkList *L){
    Node *p = (*L)->next->next, *q;
    while(p != NULL){
        q = p;
        p = p->next;
        free(q);
    }
    (*L)->next->next = NULL;
    (*L)->lenght = 0;
    return OK;
}




/**
 * 销毁单链表
*/
Status Destory(LinkList *L){
    Node *p = (*L)->next, *q;
    while(p != NULL){
        q = p;
        p = p->next;
        free(q);
    }
    free((*L));
    (*L) = NULL;
    return OK;
}




/*打印单链表表中的所有元素*/
void OutPut(LinkList L){
    
    Node *p=L->next->next ;
	for(int i=0;i<L->lenght;i++)
	{
		printf("%d ",p->data );
		p=p->next ;
	} 
    printf("\n");
}




int main()
{
    LinkList L;
    //构造单链表
    InitList(&L);
    printf("------测试插入10个数------\n");
    for(int i = 1; i<=10;i++){
        ListInsert(&L,i,i);
    }
    OutPut(L);
    printf("------删除第5位的数据------\n");
    ElemType elem;
    ListDelete(&L, &elem, 5);
    OutPut(L);
    printf("------清空单链表------\n");
    Clear(&L);
    OutPut(L);
}

四、静态链表

1、静态链表的基本概念

  静态链表，使用数组连描述指针，首先我们让数组的元素都是由两个数据域组成，data和cur。数据域data，用来存放数据元素；游标cur相当于单链表的next指针，存放该元素的后继在数组中的下标。

为了方便插入数据，我们通常会把数组建立得大一些，以便有一些空闲空间可以便于插入时不至于溢出。
另外我们对数组的第一个和最后一个元素作为特殊元素处理，不存数据。通产把未被使用的数组元素称为备用链表。而数组第一个元素，即下标为0的元素的cur存放备用链表的第一个结点的下标；而数组的最后一个元素的cur则存放第一个有数值的元素的下标，相当于单链表中的头结点的作用，当整个链表为空时，则为0。

2、静态链表的插入操作

例如如果我们需要在“乙”和“丁”之间，插入一个“丙”，操作如图所示：

3、静态链表的删除操作

例如如果要删除“甲”元素，如图所示：

五、循环链表

1、循环链表的基本概念

将单链表中终端节点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表。
循环链表带有头结点的空链表如下图所示：

对于非空的循环链表则如下图所示：

2、仅设尾指针的循环链表

上述仅设头指针的循环链表有一个弊端，我们可以用O(1)的时间访问第一个节点，但对于最后一个节点，却需要O(n)的时间，于是就有了仅设尾指针的循环链表。

如下图所示：
从上图可以看到，终端节点用尾指针rear指示，则查找终端节点是O(1)，而开始节点，其实就是rear->next->next，其时间复杂度也是O(1)。

举个程序的例子，要将两个循环链表合成一个表时，有了尾指针就非常简单了。比如下面的这两个循环链表，它们的尾指针分别是rearA和rearB。

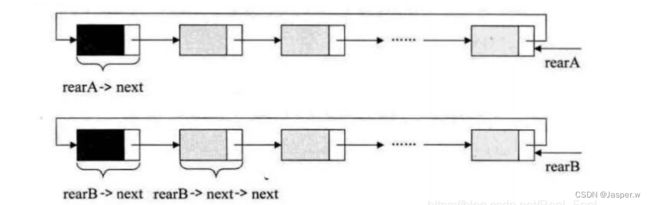
要想把它们合并，只需要如下操作即可：

六、双向链表

1、双向链表的基本概念

双向链表（double linked list）是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域，一个指向直接后继，另一个指向直接前驱。

双链表示意图如下所示：

2、双向链表的插入操作

在双链表中p所指的结点之后插入结点*s，其指针的变化过程如下图所示：

3、双向链表的删除操作

如果要删除q结点，只需下面两步：

总结

一、顺序表和链表的比较

1、存取(读写)方式

顺序表可以顺序存取,也可以随机存取,链表只能从表头顺序存取元素。例如在第i个位置上执行存或取的操作,顺序表仅需一次访问,而链表则需从表头开始依次访问i次。

2、逻辑结构与物理结构

采用顺序存储时,逻辑上相邻的元素,对应的物理存储位置也相邻。而采用链式存储时,逻辑上相邻的元素,物理存储位置则不一定相邻,对应的逻辑关系是通过指针链接来表示的。

3、查找、插入和删除操作

对于按值查找,顺序表无序时,两者的时间复杂度均为O(n);顺序表有序时,可采用折半查找,此时的时间复杂度为O(log2n)。
对于按序号查找,顺序表支持随机访问,时间复杂度仅为O(1),而链表的平均时间复杂度为O(n)。顺序表的插入、删除操作,平均需要移动半个表长的元素。链表的插入、删除操作,只需修改相关结点的指针域即可。由于链表的每个结点都带有指针域,故而存储密度不够大。

4、空间分配

顺序存储在静态存储分配情形下,一旦存储空间装满就不能扩充,若再加入新元素,则会出现内存溢出,因此需要预先分配足够大的存储空间。预先分配过大,可能会导致顺序表后部大量闲置;预先分配过小,又会造成溢出。动态存储分配虽然存储空间可以扩充,但需要移动大量元素,导致操作效率降低,而且若内存中没有更大块的连续存储空间,则会导致分配失败。链式存储的结点空间只在需要时申请分配,只要内存有空间就可以分配,操作灵活、高效。

二、在实际中应该怎样选取存储结构呢?

1、基于存储的考虑

难以估计线性表的长度或存储规模时,不宜采用顺序表;链表不用事先估计存储规模,但链表的存储密度较低,显然链式存储结构的存储密度是小于1的。

2、基于运算的考虑

在顺序表中按序号访问a1的时间复杂度为O(1),而链表中按序号访问的时间复杂度为O(n)因此若经常做的运算是按序号访问数据元素,则显然顺序表优于链表。
在顺序表中进行插入、删除操作时,平均移动表中一半的元素,当数据元素的信息量较大且表较长时,这一点是不应忽视的;在链表中进行插入、删除操作时,虽然也要找插入位置,但操作主要是比较操作,从这个角度考虑显然后者优于前者。

3、基于环境的考虑

顺序表容易实现,任何高级语言中都有数组类型;链表的作是基于指针的,相对来讲,前者实现较为简单,这也是用户考虑的一个因素。
总之,两种存储结构各有长短,选择哪一种由实际问题的主要因素决定。通常较稳定的线性表选择顺序存储,而频繁进行插入、删除操作的线性表(即动态性较强)宜选择链式存储。
注意:只有熟练掌握顺序存储和链式存储,才能深刻理解它们各自的优缺点。