低差异序列（二）- 高效实现以及应用

低差异序列（二）- 高效实现以及应用

https://zhuanlan.zhihu.com/p/20374706

上一篇专栏文章（低差异序列（一）- 常见序列的定义及性质）介绍了几种常见低差异序列的定义和性质。低差异序列可以快速的生成高质量分布，Stratified和Latin Hypercube的样本分布。对于蒙特卡洛程序来说，使用低差异序列生成样本相比伪随机数会有更高的收敛效率，例如题图左侧为Sobol序列32个样本渲染，右侧为伪随机数，可以看出右侧的噪点要比左侧更加明显。这一篇文章会继续简单介绍一下它们的实现以及应用中需要解决的问题。

Radical Inversion实现

目前介绍过的所有序列都基于Radical Inversion这个操作，而这个操作尽管公式略微复杂，但它的实现非常直观和简单，下面贴上代码以及注释。

double IntegerRadicalInverse(int Base, int i)
{
	int numPoints, inverse;
	numPoints = 1;
	// 此循环将i在"Base"进制下的数字左右Flip
	for(inverse = 0; i > 0; i /= Base)
	{
		inverse = inverse * Base + (i % Base);
		numPoints = numPoints * Base;
	}

	// 除以Digit将这个数镜像到小数点右边
	return inverse / (double) numPoints;
}

当整数的bits不够用时，Radical Inversion也可以用基于浮点数来实现。

double RadicalInverse(int Base, int i)
{
	double Digit, Radical, Inverse;
	Digit = Radical = 1.0 / (double) Base;
	Inverse = 0.0;
	while(i)
	{
		// i余Base求出i在"Base"进制下的最低位的数
		// 乘以Digit将这个数镜像到小数点右边
		Inverse += Digit * (double) (i % Base);
		Digit *= Radical;

		// i除以Base即可求右一位的数
		i /= Base;
	}
	return Inverse;
}

可以试着复制上面的函数随便调用一下看一下返回值的Pattern，Radical Inversion的实现就是这么简单。

Halton, Hammersley实现

实现了Radical Inversion之后，Halton就只是找到互为质数的数字作为Base调用RadicalInverse就可以了。Hammersley则和Halton几乎一样，只是第一维是uniform分布而已。

double Halton(int Dimension, int Index)
{
	// 直接用第Dimension个质数作为底数调用RadicalInverse即可
	return RadicalInverse(NthPrimeNumber(Dimension), Index);
}
double Hammersley(int Dimension, int Index, int NumSamples)
{
	// Hammersley需要事先确定样本的总数
	if (Dimension == 0)
		return Index / (double) NumSamples;
	else
		return RadicalInverse(NthPrimeNumber(Dimension-1), Index);
}

然而这样的实现存在一些问题。1）在上一篇文章里提到过，Halton序列在底数较大的时候样本个数会有很严重的correlation。所以需要采用Scrambling来解决这个问题。2）RadicalInverse的实现的效率依赖于一个循环，将索引Index的数字左右颠倒。这一步骤可以通过一次将多个连续数字的左右颠倒连同Faure Scrambling预计算出来，存在一个查找表里。运行的时候直接将索引的多个数字提取出来，然后直接查表得到结果。下面给出一段以5作为底数的Halton序列实现。

// Faure Scrambling以5为底数的permutation为[0,3,2,1,4]
// 下面长度为5^3数组一次可以完成三个数字的permute
static const unsigned short FaurePermutation[5*5*5] = { 0, 75, 50, 25, 100, 15, 90, 65, 40, 115, 10, 85, 60, 35, 110, 5, 80, 55,
30, 105, 20, 95, 70, 45, 120, 3, 78, 53, 28, 103, 18, 93, 68, 43, 118, 13, 88, 63, 38, 113, 8, 83, 58, 33, 108,
23, 98, 73, 48, 123, 2, 77, 52, 27, 102, 17, 92, 67, 42, 117, 12, 87, 62, 37, 112, 7, 82, 57, 32, 107, 22, 97,
72, 47, 122, 1, 76, 51, 26, 101, 16, 91, 66, 41, 116, 11, 86, 61, 36, 111, 6, 81, 56, 31, 106, 21, 96, 71, 46,
121, 4, 79, 54, 29, 104, 19, 94, 69, 44, 119, 14, 89, 64, 39, 114, 9, 84, 59, 34, 109, 24, 99, 74, 49, 124 };
double Halton5(const unsigned Index)
{
	// 依次提取0-2,3-5,6-8，9-11位的digits左右翻转并移到小数点右边
	return (FaurePermutation[Index % 125u] * 1953125u + FaurePermutation[(Index / 125u) % 125u] * 15625u +
FaurePermutation[(Index / 15625u) % 125u] * 125u +
FaurePermutation[(Index / 1953125u) % 125u]) * (0x1.fffffep-1 / 244140625u);
}

上面的实现没有任何分支，并且所有的计算就是几次求余和一个小的数组访问，要比一开始的版本高效许多，更重要的是Scrambling的问题也一并解决了。Faure Scrambling的具体计算方法，以及完整的实现可以在Leonhard的网页找到：http://gruenschloss.org/

Sobol实现

Sobol序列的所有维度都是基于2为底数的Radical Inversion。只不过每个维度有自己不同的生成矩阵（Generator Matrix）。因为是以2为底数，将数字从二进制中提取每一位的数字，以及和矩阵做运算，都可以用位操作（右移，异或等）来完成，非常高效。

double Sobol(uint64 i, uint Dimension)
{
	double r;
	// 将i依次右移，提取2进制里的每一位
	for (uint k = 0; i; i >>= 1, k++)
		if (i & 1) // 若当前位为1，则用异或和矩阵相乘
			r ^= C[Dimension][k];
	return r / (double) (1 << M); // 除以2^M,移到小数点右边
}

至于生成矩阵，可以在Kuo的网站Sobol sequence generator 找到最高维度为21201的生成矩阵。

渲染中的应用

光线的传递的模拟基于蒙特卡洛积分，每一个像素都需要数千个样本，根据模拟算法的不同，每一个样本都是一个维度空间中的一个点。低差异序列要应用在渲染中需要解决的一个问题就是如何把一个低差异序列用到每一帧画面里的数百万个像素中去。有一种非常简单的方法叫做Cranley-Patterson Rotation。它的做法是每个像素先各生成完全一样的样本点集，生成之后对每个像素的点集随机生成一个不同的Shift，如果有任何值Shift出了[0, 1)的范围，则Modulate回到[0, 1)中。例如下图中所有样本都沿着向量移动，然后映射回[0, 1)范围。

这样做的一个问题就是会破坏地差异序列的Stratification属性。例如上图中间，原本每4x4区间中只有一个样本覆盖，在被shift只后许多区间中有两个样本。但这个方法的好处是实现非常简单，而且在一些简单的光线传递算法例如Path Tracing中效果也没有什么问题。渲染器Blender Cycle中的Sobol采样就是用的这个算法。但是当这个方法用在任何模拟双向传递的算法中（例如Bidirectional Path Tracing，Light Tracing，Photon Mapping以及其变种），从光源发出的光线会有明显的Aliasing。例如下图是把Cranley-Patterson Rotation运用在Light Tracing时的效果。这也是我意外产生过的一个非常好看的Bug：

 

所以解决这个问题的最好办法是直接用一个序列覆盖画面中的所有像素。每个像素只使用那些第1,2维刚好落在像素面的点。这样做到优势有许多，1）屏幕空间中的样本分布符合所有低差异序列的性质，Stratified，Latin Hypercube，Low Discrepancy。2）像素间的样本因为是同一个序列中不同的点，所以最后的结果不会有任何Aliasing。3）Halton和Sobol都可以非常高效的根据像素的索引计算出此像素的样本索引，所以自然的支持任何progressive或者adaptive的采样。至于如何求出落在像素范围内的样本索引，可以参考这篇论文：http://gruenschloss.org/sample-enum/sample-enum.pdf

 

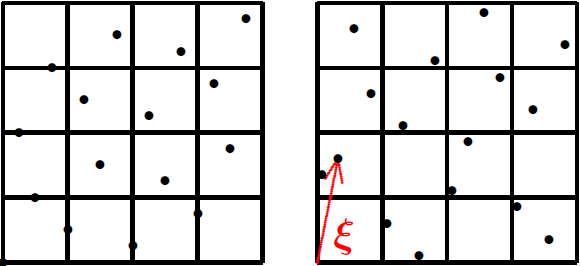
光线传递模拟的另一个常见的问题是，渲染方程各个某些维度的方差有大有小，意味着各个维度收敛需要的样本数量也各不相同。例如屏幕空间的锯齿，通常32-64个样本即可做到非常平滑的收敛，但是一个面积非常大的面光源阴影则可能需要~1000个样本才能得倒无噪点的结果，亦或者环境遮挡，粗糙材质或者环境光源等。低差异序列也可以非常好的支持这种维度分散的模式。有一种方法叫做Trajectory Splitting，即对一个地差异序列在某一些维度上采样的频率高于其他维度，如下图右边所示。

 

这种方法在实现上也非常的简单，只需要将索引除以样本数量的倍数即可（上图例子中是4，如果是用以2为底数的Sobol，将索引右移两位即可）。

 

除了这些以外，低差异序列因为生成的点集因为完全Deterministic，非常适合并行，无论是单系统的多线程，还是多节点的云端渲染。例如每个第一线程可以选择第1-1000个样本，第二个线程1001-2000，依此类推，最后将线程间的结果平均以后保证会得到正确的收敛结果。

Conclusion

粗略总结一下，低差异序列可以非常高效的生成分布非常均匀的高质量样本集合，相比伪随机数极大的提高蒙特卡洛积分收敛的效率。并且它们的实现都不复杂，除了Hammersley点集以外，其余对progressive渲染都非常友好。生成的点集是deterministic的，没有任何随机性，也非常适合多线程并行（CPU，GPU，网络等）。通过像素的索引计算出样本的索引可以用一个序列覆盖整个画面，运用这一点又可以实现屏幕空间的Adaptive采样。实在是找不到什么理由不去用了 ；）

 

Reference：

http://web.maths.unsw.edu.au/~josefdick/MCQMC_Proceedings/MCQMC_Proceedings_2012_Preprints/100_Keller_tutorial.pdf

http://gruenschloss.org/sample-enum/sample-enum.pdf

http://www.uni-kl.de/AG-Heinrich/EMS.pdf

编辑于 2015-12-06