LeetCode刷题之1838. 最高频元素的频数

元素的 频数 是该元素在一个数组中出现的次数。

给你一个整数数组 nums 和一个整数 k 。在一步操作中，你可以选择 nums 的一个下标，并将该下标对应元素的值增加 1 。

执行最多 k 次操作后，返回数组中最高频元素的 最大可能频数 。

示例 1：

输入：nums = [1,2,4], k = 5
输出：3
解释：对第一个元素执行 3 次递增操作，对第二个元素执 2 次递增操作，此时 nums = [4,4,4] 。
4 是数组中最高频元素，频数是 3 。

示例 2：

输入：nums = [1,4,8,13], k = 5
输出：2
解释：存在多种最优解决方案：
- 对第一个元素执行 3 次递增操作，此时 nums = [4,4,8,13] 。4 是数组中最高频元素，频数是 2 。
- 对第二个元素执行 4 次递增操作，此时 nums = [1,8,8,13] 。8 是数组中最高频元素，频数是 2 。
- 对第三个元素执行 5 次递增操作，此时 nums = [1,4,13,13] 。13 是数组中最高频元素，频数是 2 。

本题我有两种解法，一是滑动窗口，二是前缀和+二分。

一、滑动窗口

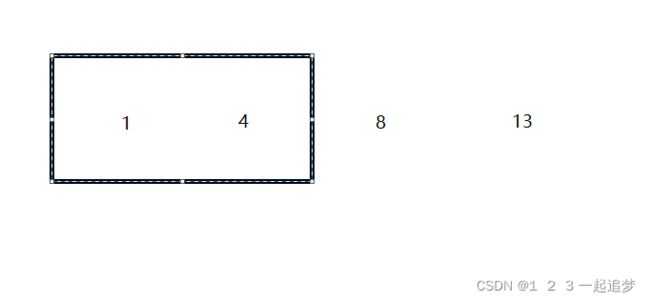
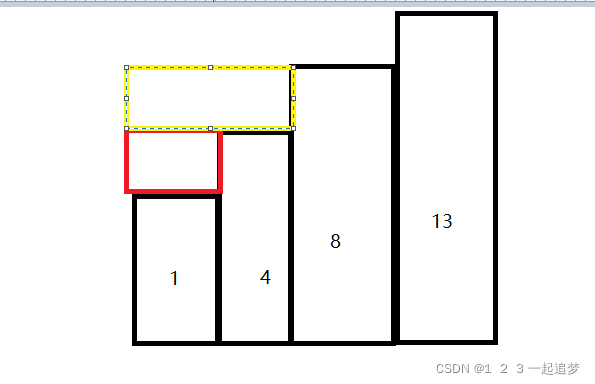
在进行前我们需先对数组排序，既然是滑动窗口，就有左边界和右边界。起始我们把边界锁定到下标0，1。用max保存最大高频数的操作次数，初始值为1。上如图所示:

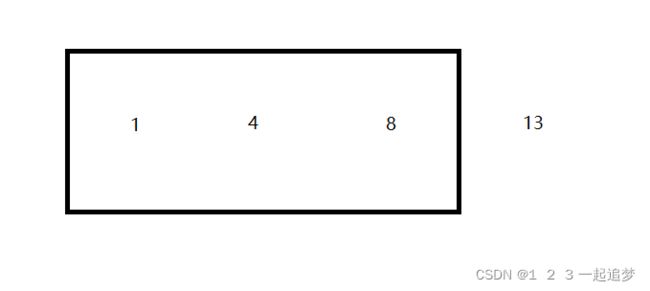
 此时最大数为4，前面变成4需操作3次明显小于k,然后让右边界往右挪一位，再判断以8为边界的区间的操作次数。更新max为2。

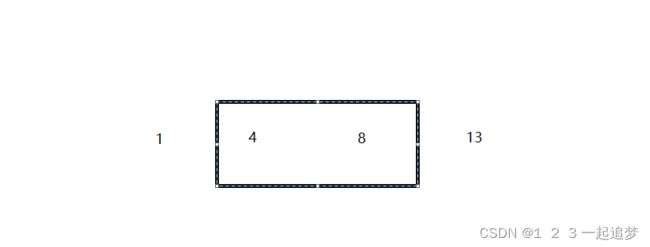
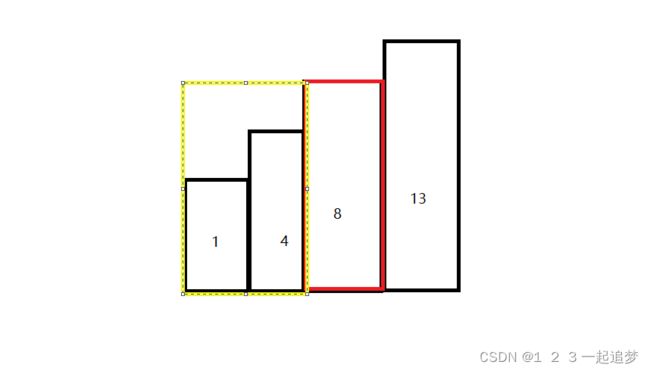
 此次的操作次数为11，明显大于k。这时我们让左边界往前挪一位。

此时 操作次数为4明显小于k，但不用更新操作次数，因为还是2个数。然后，让右边界继续挪一位。

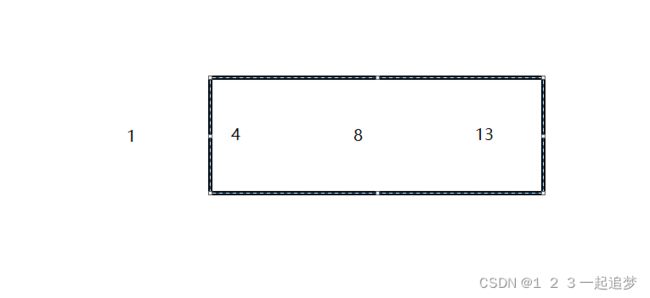
 很明显操作次数14已经大于K,让左边界挪直到操作次数小于k，但左边界要小于右边界。很明显，此时已经结束，max为2。也是我们需要的答案了。

滑动窗口的基本思路就是上面的步骤，然后再简单说下如何求操作次数。

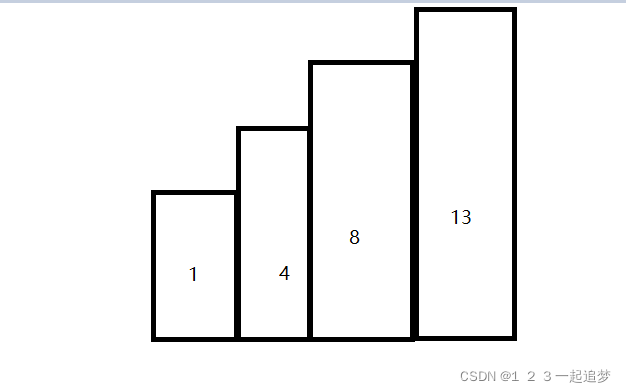
 用上面柱形图，解释下如何求总操作次数sum。如上图，当窗口里只有1 4，sum+=4-1。

 很明显4-1就是上面红色那块，当窗口把8放进去后，我们只需要求出黄色那块，就可以得到以8为边界的操作次数，黄色那块也就是（8-4）*2,总操作次数也就是sum+=（8-4）*2。总体思路就是这样。下面是代码:

class Solution {
    public int maxFrequency(int[] nums, int k) {
        Arrays.sort(nums);

        int left=0,max=1,right;

        long sum=0;

        for(right=1;rightk){
                
                sum-=nums[right]-nums[left];

                left++;
            }

            max=Math.max(max,right-left+1);//更新max

        }
        return max;
    }
}

二、前缀和+二分

这种方法也是要先排序，然后我们创建新数组保存前缀和，下标0代表标0项和，1代表前一项和，以此类推。二分要找的的数也就是左边界，我们需先锁定右边界，然后再0~右边界中找左边界，找到零界点，就是当前右边界下，最多高频数的区间，以此类推不断推进右边界，直到数组最后一个元素。关于操作次数，据需要配合前缀和来求，我简单用图来解释下。如下图所示：

如上图所示，我们已8为边界，然后可以得知总操作次数，8*2-（前两项前缀和-前零项前缀和）此表达式求出的就是总操作次数。以下是代码：

class Solution {
    public int maxFrequency(int[] nums, int k) {

        Arrays.sort(nums);
       
        long res[]=new long[nums.length+1];
        res[0]=0;
        for(int i=1;i

还有什么好的解决方法，请大佬分享。