算法之克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔(Kruskal)算法,是用来求加权连通图的最小生成树的算法。
基本思想:按照权值从小到大的顺序选择n-1条边,并保证这n-1条边不构成回路
具体做法:首先构造一个只含n个顶点的森林,然后依权值从小到大从连通网中选择边加入到森林中,并使森林中不产生回路,直至森林变成一棵树为止
克鲁斯卡尔算法在所有连接森林的两个不同树的边里面,寻找权值最小的边将最小的边加入一个不相交的集合来进行维护,每次加入时判断该边的起始顶点与结束顶点是否属于同一个树,即是否使森林产生回路,如果不产生回路则加入集合
其对应伪代码如下:

其算法描述:
1-3 行将集合A初始化一个空集合,创建一棵树V;
4 行 对邻边进行排序
5-8行 循环对边按权重从低到高进行检查,从每条边的起点和终点进行检查,判断是否构成回路,没有形成回路则将边加入集合中
要点: 对边排序;判断是否形成回路;若没有回路则每次选择权值最小的边加入集合—这里体现了贪心算法的思想;
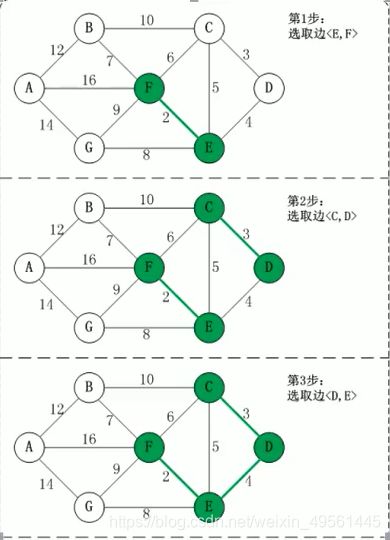
1 选取权值最小的E-F边加入集合,E-F第一次加入肯定不会存在回路
2 选择权值第二小的C-D边放入集合,检查是否形成回路
3 选取D-E加入集合
4 当选取较小的边C-E时,发现C-D-E在集合中会形成回路,所以C-E不能加入集合
判断回路其实也简单:循环集合,从C-E边的起始顶点C和终点E出发,如果形成回路则
顶点C和顶点E必然共用同一终点。
5 重复 1 2 3 4 将B-F E-G A-B加入集合,最小生成树构建完成
代码实现
我们使用邻接表构建图
class Graph<T>{
int vertexNum;
int edgeNum;
ArrayList< Edge<T>> edgesList ;
ArrayList< Vertex<T>> vertexList;
public Graph(T[] vertex){
vertexList = new ArrayList<>();
edgesList = new ArrayList<>();
this.addVertex(vertex);
}
static class Vertex<T> {
T verName;//节点存储的内容
Edge<T> edgeLink ;//顶点的边链
public Vertex(T name){
verName = name;
edgeLink = null;
}
@Override
public String toString() {
return "Vertex{" +
"verName=" + verName +
'}';
}
}
static class Edge<T> {
Vertex<T> start;//边的头节点
Vertex<T> end;//边的尾部节点
int weight;//边的权值
Edge<T> broEdge;// 节点连接的其他边,指向下一个邻接点
public Edge(Vertex<T> start, Vertex<T> end,int weight){
this.start = start;
this.end = end;
this.weight = weight;
}
@Override
public String toString() {
return "Edge{" +
"start=" + start +
", end=" + end +
", weight=" + weight +
'}';
}
}
public void addVertex(T[] vertex){
for (T c : vertex) {
vertexList.add(new Vertex<>(c));
}
vertexNum = vertex.length;
}
public void addEdge(T start,T end,int weight){
Vertex<T> startVertex = getVertex(start);
Vertex<T> endVertex = getVertex(end);
edgesList.add(concatEdge(startVertex, endVertex,weight));
concatEdge(endVertex, startVertex,weight);
edgeNum++;
}
private Edge<T> concatEdge(Vertex<T> startVertex, Vertex<T> endVertex, int weight){
Edge<T> edge = new Edge<>(startVertex,endVertex,weight);
if (startVertex.edgeLink != null){
Edge<T> broEdge = startVertex.edgeLink;
while (broEdge.broEdge != null){
broEdge = broEdge.broEdge;
}
broEdge.broEdge = edge;
}
else{
startVertex.edgeLink = edge;
}
return edge;
}
public Vertex<T> getVertex(T verName){
return vertexList.stream().filter(e -> e.verName.equals(verName)).findFirst().orElseThrow(()->new NoSuchElementException(verName+" is no present"));
}
}
求解最小生成树
public LinkedList<Graph.Edge<Character>> kruskal(Graph<Character> graph){
ArrayList<Graph.Edge<Character>> edgesList = graph.edgesList;
edgesList.sort(Comparator.comparingInt(o -> o.weight));
LinkedList<Graph.Edge<Character>> minTree = new LinkedList<>();
int[] ends = new int[graph.edgeNum]; //用于保存"已有最小生成树" 中的每个顶点在最小生成树中的终点
for (Graph.Edge<Character> edge : edgesList) {
int p1 = getIndex(graph.vertexList, edge.start);
int p2 = getIndex(graph.vertexList, edge.end);
//获取p1这个顶点在已有最小生成树中的终点
int m = loop(ends, p1);
//获取p2这个顶点在已有最小生成树中的终点
int n = loop(ends, p2);
if (m != n) {
minTree.add(edge);
ends[m] = n;//将该边的起始顶点和终点进行连接,代表该边已经在最小生成树里
}
}
return minTree;
}
private int loop(int[] ends, int i ) {
while (ends[i] != 0) {
i = ends[i];
}
return i;
}
private int getIndex(ArrayList<Graph.Vertex<Character>> vertexList,Graph.Vertex<Character> vertex ) {
for(int i = 0; i < vertexList.size(); i++) {
if(vertexList.get(i) == vertex) {
return i;
}
}
return -1;
}