力扣题解-1579. 保证图可完全遍历(并查集)
题目:1579. 保证图可完全遍历
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
类型 1:只能由 Alice 遍历。
类型 2:只能由 Bob 遍历。
类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:

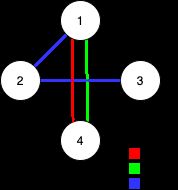
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3:

输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。
提示:
- 1 <= n <= 10^5
- 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
- edges[i].length == 3
- 1 <= edges[i][0] <= 3
- 1 <= edges[i][1] < edges[i][2] <= n
- 所有元组 (typei, ui, vi) 互不相同
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解
题目要求无向图可完全遍历即为无向图为连通图。因此,图的连通性可以利用并查集来解决。
求解并查集中可以删除的最大边数,实际上等价于求解可以利用的最小边数使得无向图的节点构成的并查集是连通的。
由于图中存在三种类型的边,type=3的边“最为强大”,Alice 和 Bob都可以连通,所以先将type=3的边输入到并查集中进行合并。
那么,合并成功则说明该条边是有效的边,可以连通这两个节点;合并失败则说明该条边是冗余边,可以删除(对应代码中ans++)。
type=1和type=2的边,处理上也类似。但是,这两类边进行合并时,使用的并查集是来自于上面得到的同一个并查集结果,因此,需要对并查集进行拷贝。
三类边遍历完后,如果两个并查集都是连通的,则表明可以遍历(返回ans),否则无法遍历(返回-1)。
代码
class UnionFind {
private:
int n;
vector<int> parent;
public:
UnionFind(int n_): n(n_) {
parent.resize(n);
for(int i = 0; i < n; i++) {
parent[i] = i;
}
}
UnionFind(UnionFind & uf) {
n = uf.n;
parent.resize(uf.parent.size());
for(int i = 0; i < parent.size(); i++) {
parent[i] = uf.parent[i];
}
}
int find(int x) {
int root = x;
while(root != parent[root]) {
root = parent[root];
}
while(x != parent[x]) {
int tmp = parent[x];
parent[x] = root;
x = tmp;
}
return root;
}
bool merge(int x, int y) {
int px = find(x);
int py = find(y);
if(px == py) {
return false;
}
parent[py] = px;
n--;
return true;
}
int getSetNum(void) {
return n;
}
};
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
UnionFind unionFind(n);
int ans = 0;
for(int i = 0; i < edges.size(); i++) {
int type = edges[i][0];
if (type != 3) {
continue;
}
int u = edges[i][1] - 1;
int v = edges[i][2] - 1;
if(unionFind.merge(u, v) == false) {
ans ++;
}
}
UnionFind unionFind_alice(unionFind);
for(int i = 0; i < edges.size(); i++) {
int type = edges[i][0];
int u = edges[i][1] - 1;
int v = edges[i][2] - 1;
if (type == 1) {
if(unionFind_alice.merge(u, v) == false) {
ans ++;
}
} else if(type == 2) {
if(unionFind.merge(u, v) == false) {
ans ++;
}
}
}
if(unionFind_alice.getSetNum() == 1 and unionFind.getSetNum() == 1) {
return ans;
}
return -1;
}
};