力扣题解-1631. 最小体力消耗路径(并查集)
题目:1631. 最小体力消耗路径
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
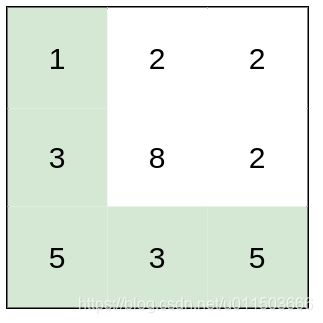
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
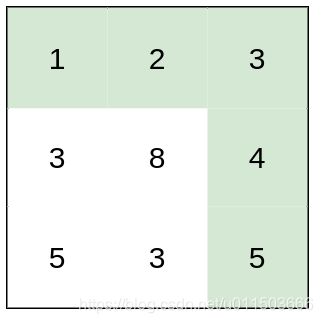
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
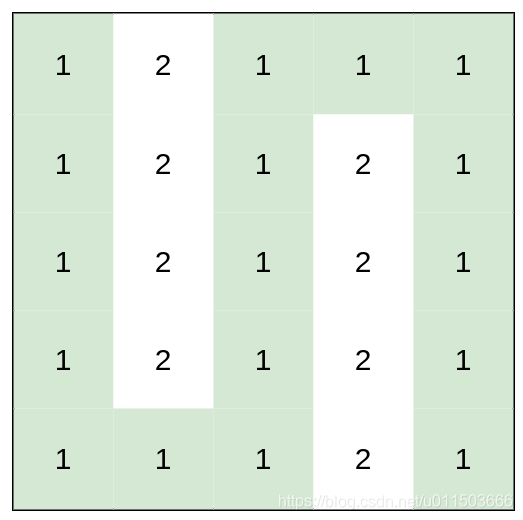
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-with-minimum-effort
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解
将网格看作是无向图,那么本题的目标就为求当顶点(0,0)和顶点(rows-1,columns-1)连通时,所有路径中边的最大权值是最小的一条路径对应的边的最大权值。
本题中的”体力消耗“实际上限制了无向图中相邻顶点之间的连通性,即当“体力消耗”大于等于两个相邻顶点的高度差的绝对值时,这两个顶点是连通的。
因此,我们利用并查集来求解,我们将无向图的边按照权值进行从小达到排序,依次按照边进行顶点的合并,直至顶点(0,0)和顶点(rows-1,columns-1)连通,此时的权值为答案。
代码
class UnionFind {
private:
int n;
vector<int> parent;
public:
UnionFind(int n_): n(n_) {
parent.resize(n);
for(int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int x) {
int root = x;
while(root != parent[root]) {
root = parent[root];
}
while(x != parent[x]) {
int tmp = parent[x];
parent[x] = root;
x = tmp;
}
return root;
}
bool merge(int x, int y) {
int px = find(x);
int py = find(y);
if(px == py) {
return false;
}
parent[py] = px;
return true;
}
};
bool func(tuple<int, int, int> &tp1, tuple<int, int, int> &tp2) {
int value1 = std::get<2>(tp1);
int value2 = std::get<2>(tp2);
return value1 < value2;
}
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
//按照无向边权值由小到大加入到并查集中,直到(0,0)与(n*n-1)属于同一集合
int rows = heights.size();
int columns = heights[0].size();
vector<tuple<int, int, int>> edges;//无向边
for(int i = 0; i < rows; i++) {
for(int j = 0; j < columns; j++) {
int u = i*columns + j;
//构建无向图的边时,由于两个顶点的边(u,v)是没有方向,因此只要存储其中一条即可
if(i-1 >= 0) {
int v = (i-1)*columns + j;
edges.push_back(std::make_tuple(u, v, abs(heights[i][j] - heights[i-1][j])));
}
if(j-1 >= 0) {
int v = i*columns + j-1;
edges.emplace_back(u, v, abs(heights[i][j] - heights[i][j-1]));
}
}
}
//按照权值排序
sort(edges.begin(), edges.end(), func);
int ans = 0;
UnionFind unionFind(rows*columns);
for(auto& edge: edges) {
int x = std::get<0>(edge);
int y = std::get<1>(edge);
ans = std::get<2>(edge);
unionFind.merge(x, y);
if(unionFind.find(0) == unionFind.find(rows*columns-1)) {
break;
}
}
return ans;
}
};