算法基础之二维差分 学习笔记

更新啦~

二维差分

我们一样先从题目来插入
 首先 
输入用例为： 

3 4 2
1 2 3 4
5 6 7 8
9 10 11 12
1 1 1 4 1
1 1 2 4  -2

表示的是输入3行4列个数并进行2次查询
然后是3行4列个数
最后查询是从第1，1到第1，4的二维数组加上1，输出此时的数列

为了方便我把初始的坐标称为x1,y1  终点坐标x2,y2，增加的数为l

并把原数据存入N[3][4]里面，增加的数存在a[3][4]中，最后增加的数存在sum【3】【4】

 同样的遇到这种题目 暴力破解可以，直接从1，1到1，4的数组都加v就行

但是如果数列比较大而查询的次数又比较多，别如10个数查询50次

每次遍历1遍，需要500次，就会使得算法复杂度为O（n*m）

所以为了优化算法，降低复杂度，就出现了二维差分

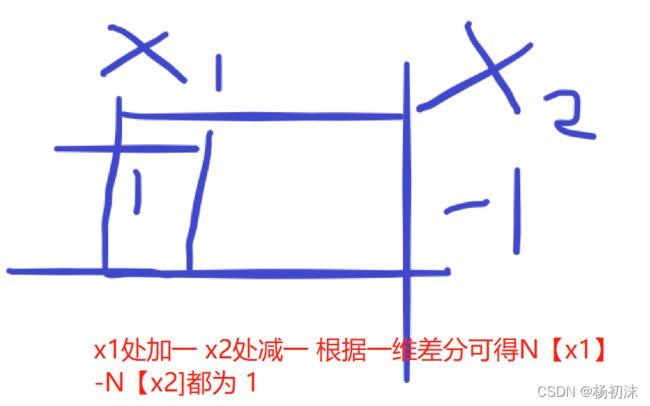
首先一维思想是一行

同理当为一列时也是这样的

 

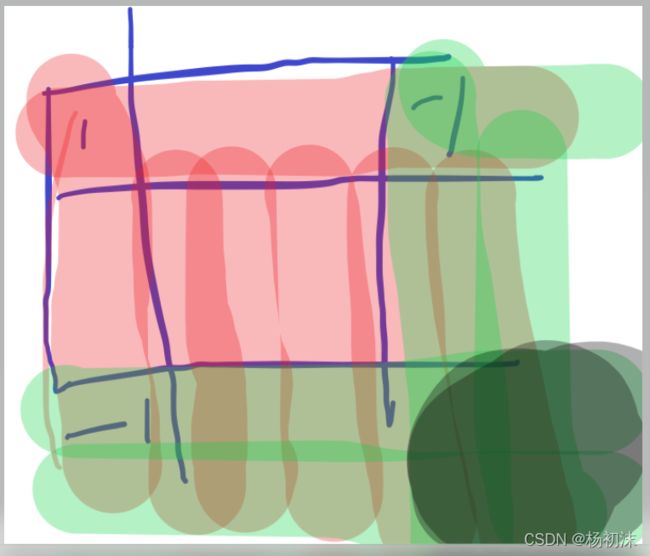
当放在二维时累加就会使整个粉色区域都加1

 根据一维思想我们在行和列都设了一个-1 即绿色区域覆盖处

不难看出那个深绿色被减了两次所以加上一个深绿色即加1

所以二维差分的公示就出来了

    a[x1][y1]+=l;
    a[x2+1][y1]-=l;
    a[x1][y2+1]-=l; 
    a[x2+1][y2+1]+=l;

只要用二维前缀和求矩阵和思想，得到的就是N[x1][y1]-N[x2][y2]都加l 

#include
int N[100][100];
int a[100][100];
int sum[100][100];
int add(int x1,int y1,int x2,int y2,int l)
{
	a[x1][y1]+=l;
	a[x2+1][y1]-=l;//注意两个点即行和列都要设-l 也就是传递值的终止信号 
	a[x1][y2+1]-=l; 
	a[x2+1][y2+1]+=l;//对角线个矩阵减了两次所以加l 
}
void Sum(int n,int m)//二维前缀和思想 得到的就是N[x1][y1]-N[x2][y2]都加l 
{
		for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];//值传递 
	}
 } 
int main()
{
	int n,m,M;
	scanf("%d %d %d",&n,&m,&M);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		scanf("%d",&N[i][j]);
	}
	int x1,y1,x2,y2,l;
	while(M--)
	{
		scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&l);
		add(x1,y1,x2,y2,l);
	}
	Sum( n, m);
		for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
	printf("%d ",sum[i][j]+N[i][j]); 
	printf("\n");
	}
	
	
 } 

这篇文章以互相学习为主，有什么错的还望告知，谢谢啦

（ps 小声bb，如果有很多人看的话，我就会持续更新算法基础哦，写博客真的很累，emmm....）