算法基础：前缀和+差分+离散化+区间合并

给予我多的思考，一为大佬的博客，点这里！

前缀和

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

1,一维数组前缀和

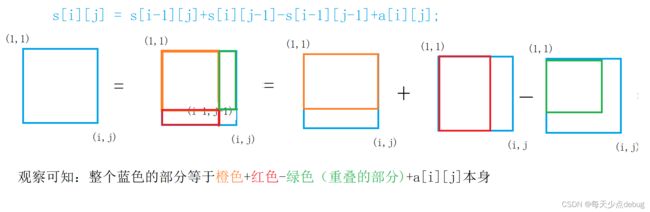
2,二维数组前缀和

s[i][j]是以第i行第j列点的左上半部分所有元素的和，并不是和一维数组一样s[i][j]直接表示从(1,1)到（i,j)的中间没有间隔的和！

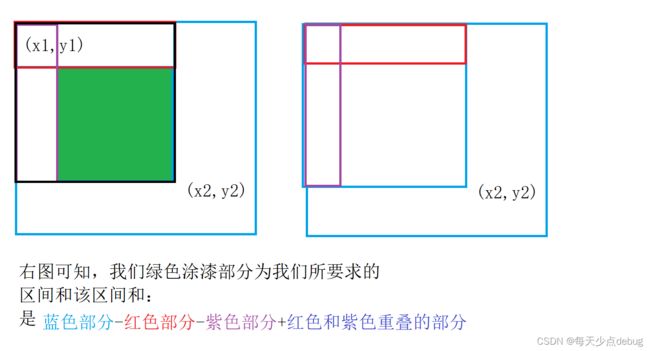
3，二维数组区间前缀和

我们再来画图计算一下左上角坐标(x1,y1)到右下角坐标(x2,y2)间区间和如何计算：

差分

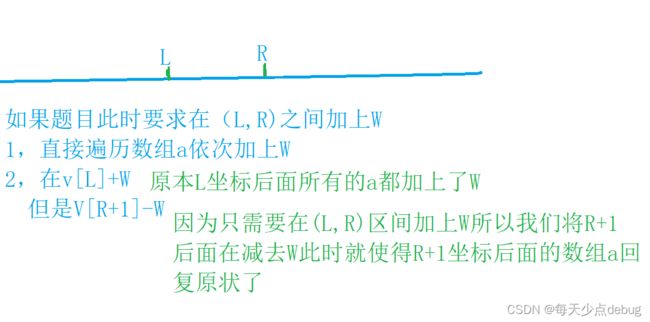
1， 一维差分

题目链接：一维差分
首先我们确定一个数组a:a[1]a[2]....a[N]
再构造一个差分数组v:v[1]v[2]v[3]v[4]
且必须使得他们满足性质a[i]等于v数组前i个数之和
则a数组是v数组的前缀和数组，但v数组是a数组的差分数组
注意由于差分很多都得用到我上面讲到的前缀和，所以我们的数组下标都应该设置为1
如何创造差分数组?

我们创造了这个数组有什么用呢？
看题目：
输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2

由题意可知，我们如果很暴力的直接枚举a数组直接相加的话，大概率会超时，这个时候就可以用到差分数组了，时刻记住一件事，a数组是v数组的前缀和！

#include
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N],n,m;
void insert(int l, int r, int c)//构建差分数组
{
	b[l] += c;
	b[r + 1] -= c;
}
int main()
{
	cin >> n >> m;
	int i = 0;
	for (i = 1; i <= n; i++)
	{
		cin >> a[i];
		b[i] = a[i] - a[i - 1];//这是构建差分数组的一种方式
		insert(i,i,a[i]);//还可以直接构建，可以直接构建是因为，此时假设原
		//来的数组的值都是0，此时在各个区间加上a[i]
	}
	
	while (m--)
	{
		int l, r, c;
		cin >> l >> r >> c;
		insert(l, r, c);
	}
	for (i = 1; i <= n; i++)
	{
		a[i] = b[i] + a[i - 1];
		printf("%d ", a[i]);
	}

	return 0;
}

二维数组差分

题目链接:差分矩阵
先看题：
输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2

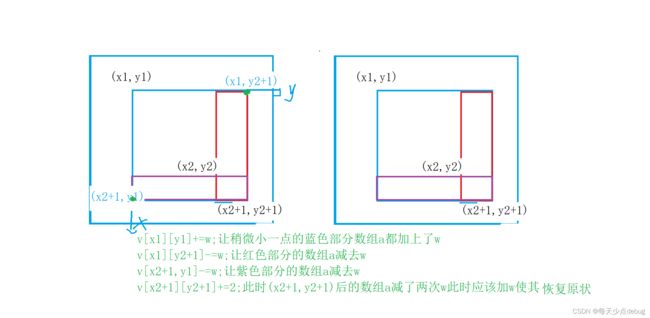
假设有数组a,v都是二维数组，v数组是a数组的差分数组。如何构建？
一维数组还可以这样

二维数组？
其实并不需要构建，因为我们在利用差分数组对原数组进行修改的时候已经可以构建差分数组了，只不过构建差分数组的话假设起初我们的v数组的各个值都是0，此时我们在个区间(i,j)到区间(i,j)加上a[i][j]就可以了

跟一维数组的差分类似，画图解释一下二维数组如何构建差分

 #define _CRT_SECURE_NO_WARNINGS 1
#include
using namespace std;
const int N = 1010;
int arr[N][N], s[N][N];//arr为输入的数组,s为差分矩阵
int n, m, q;
void insert(int x1, int y1, int x2, int y2, int c)
{
	s[x1][y1] += c;
	s[x1][y2 + 1] -= c;
	s[x2 + 1][y1] -= c;
	s[x2 + 1][y2 + 1] += c;
}
int main()
{

	cin >> n >> m >> q;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			cin >> arr[i][j];
			insert(i, j, i, j, arr[i][j]);//直接构建差分矩阵
		}

	while (q--)
	{
		int x1, y1, x2, y2, c;
		cin >> x1 >> y1 >> x2 >> y2 >> c;
		insert(x1, y1, x2, y2, c);
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
//直接利用s数组构建：s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];两种方法都可以
//
          arr[i][j] = arr[i-1][j]+arr[i][j-1]-arr[i-1][j-1]+s[i][j];
			printf("%d ", arr[i][j]);
		}
		printf("\n");
	}

	return 0;
}

离散化

理解：将一些很零散的点重新分配
假设给定一个坐标轴的范围是-2e9-2e9，默认坐标轴上的值都是0，随机在坐标轴上加上随机值，让我们求某个区间的和，如何求？
可以考虑用差分，但是数组实在是太长了，会超时，所以此时我们可以考虑在创建一个i新的数组，将原来坐标轴上面的数字按照其相对位置放到新的数组中，这就是离散化。

题目： 链接：区间和

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c。

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式
第一行包含两个整数 n 和 m。

接下来 n 行，每行包含两个整数 x 和 c。

再接下来 m 行，每行包含两个整数 l 和 r。

输出格式
共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围
−109≤x≤109,
1≤n,m≤105,
−109≤l≤r≤109,
−10000≤c≤10000
输入样例：
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例：
8
0
5

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
using namespace std;
const int N = 300010;
typedef pair<int, int>PII;
int a[N];
int s[N];
vector<PII>add, query;//添加以及询问
vector<int>alls;//将数组离散化的alls
int find(int x)//二分法查找x此时在离散化后的位置
{
	int l = 0;
	int r = alls.size() - 1;
	while (l < r)
	{
		int mid = l + r >> 1;
		if (alls[mid] >= x) r = mid;
		else
			l = mid + 1;
	}
	return r + 1;

}
int main()
{
	int n, m;
	cin >> n >> m;
	int x, c;
	for (int i = 0; i < n; i++)
	{
		cin >> x >> c;
		alls.push_back(x);
		add.push_back({ x,c });

	}
	for (int i = 0; i < m; i++)
	{
		int l, r;
		cin >> l >> r;
		query.push_back({ l,r });//方便下面找到需要算的区间
		alls.push_back(l);
		alls.push_back(r);//将询问的下标也放进去然后进行排序去重，防止询问的区间为0
	}
	//离散化
	sort(alls.begin(), alls.end());//排序
	alls.erase(unique(alls.begin(), alls.end()), alls.end());//去重
	//遍历adds
	for (auto sq : add)
	{
		int x = find(sq.first);
		a[x] += sq.second;//此时数组已经添加完毕
	}
	//求数组的前缀和
	for (int i = 1; i <= alls.size(); i++)
		s[i] = s[i - 1] + a[i];
	for (auto ret : query)
	{
		int a = find(ret.first);
		int b = find(ret.second);
		cout << s[b] - s[a-1] << endl;
	}


	return 0;

}

区间合并

题目链接：区间合并
给定 n 个区间 [li,ri]，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如：[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。

输入格式
第一行包含整数 n。

接下来 n 行，每行包含两个整数 l 和 r。

输出格式
共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围
1≤n≤100000,
−109≤li≤ri≤109
输入样例：
5
1 2
2 4
5 6
7 8
7 9
输出样例：
3

 #define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
using namespace std;
const int N = 100010;
vector<pair<int, int>>sq;
int n,l,r;
void merge(vector<pair<int, int>>& sq)
{
	vector<pair<int, int>>res;//储存合并区间
	//一定得先排序，否则做不出！
	sort(sq.begin(), sq.end());//pair进行排序的时候先按first的值进行排序，再按照second进行排序！
	int st = -2e9, end = -2e9;
	//遍历sq
	for (auto num : sq)
	{

		//如果此时的end小于此时的num.first,那么便证明合并不了
		if (end < num.first)
		{
			if (end != -2e9)
				res.push_back({ st,end });
				st = num.first; end = num.second;
		}
		else
			end = max(end, num.second);//此时可以合并

	}
	//加上最后一个区间，因为最后一个区间是不用合并的，但如果此时st!=2e9这个时候区间为0
	if (st != -2e9)
		res.push_back({ st,end });
	sq = res;



}
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> l >> r;
		sq.push_back({ l,r });
	}
	merge(sq);
	cout << sq.size() << endl;
	return 0;
}